不完备信息下维修方式决策规则粗集获取方法研究

孟科，江洋溢

(1.边防学院，陕西 西安710108;2.空军装备研究院 总体论证研究所，北京100085)

规划好维修方式是实现以可靠性为中心维修策略的基础。维修方式的规划通常采用逻辑综合决断法，它简单易行，能在时间短、开支少的情况下，对设备分类，还可充分吸收专家和使用人员的意见，逐步完善分析过程［1，2］。但是，逻辑综合决断法主要是一种定性分析方法，并且专家和使用人员的意见往往带有个人的主观判断，导致分析的结果出现不确定性。粗糙集的巨大优势在于它的客观性，上下近似、属性重要度、决策规则等都可以直接从数据中得到，不需要主观参与，是一种很有潜力的不确定性研究工具。因此，本文试图将粗糙集的方法应用到维修方式的决策中，通过外场提供的实际维修工作数据，获取维修方式的决策规则。然而由于种种原因，外场提供的数据经常会有流失现象，并且在飞机研制或者试飞阶段，有很多信息暂时获取不到，比如某些设备真实的可靠性数据等。这就产生了需要从不完备信息表中提取决策规则的问题。

不完备信息下规则获取算法，很多学者进行了相应的研究［3，4，5，6］，其方法主要有两种思路。第一种思路是，根据表中样本是否为小样本，采用相应适用的数据补齐算法。第二种思路是，不区分样本量的大小，基于证据理论直接采用最大可能遗漏属性值补齐法。不管采用那种思路，在实际约简属性时，当属性较多、样本较大时，属性约简的计算复杂度高。已经证明，求取决策表所有约简或最小约简是NP问题，因此不存在可能改进的完备算法。当属性较多、样本较小时，特征的统计规律不明显，使得特征提取、决策规则产生变得困难［7］。为简化传统决策规则获取和约简算法的步骤，克服其复杂性，本文尝试在容差关系对不完备信息的“遗漏值”解释的基础上，提出第三种思路，即在不改变信息系统大小的情况下，基于不完备信息表直接获取确定性规则，并将其应用到维修方式决策规则获取上。

1 以可靠性为中心的维修方式影响因素

1.1 以可靠性为中心的维修理论

以可靠性为中心的现代维修理论认为，很多情况下定时维修并不是最有效的维修方式。采用何种方式进行维修，要根据装备及其机件的可靠性状况、不同的故障模式及故障后果、维修资源消耗等因素来确定。以可靠性为中心的维修理论一般用逻辑决断图来确定某项维修工作的维修方式。1965年，首次出现了一种初始的“逻辑决断图”方法，经完善后，1968年7月出现了“MSG-1”手册:维修的鉴定与大纲的制定［8］。自20世纪60年代以来，先后出现的逻辑决断图已有十多种，按其输出的维修工作来分，有三种维修方式，有四种或七种维修工作类型［2］。1992年，我国国家军用标准GJB1378《装备预防性维修大纲的制定要求与方法》也采用七种维修方式。这七种维修方式主要为:保养、操作人员监控、使用检查、功能检测、定时拆修、定时报废、综合工作。

1.2 维修方式影响因素

要用使用外场数据进行维修方式决策，首先要确定影响维修方式的因素，并收集外场相应的数据。对于航空机载设备，一般用安全性、可靠性、维修性、经济性、可检测性等几个因素，每个因素中又包含了若干个子因素的影响，见表1。

表1 维修方式影响因素

设备的安全性考虑的是设备发生的故障对人身以及飞机其它设备产生不利后果，有故障对人身安全的影响、故障对飞机本身影响等两个子因素。它们各有四个等级，分别为“无影响”、“有一定影响”、“有较严重影响”和“有严重的影响”。

设备可靠性是指设备在规定时间内、在规定的条件下，完成规定功能的能力，它的子因素为操作人员可靠性、设备故障规律两个。其中，设备故障规律有四个等级，分别为“无规律”、“一般”、“有规律”和“规律性强”;操作人员可靠性分为“不熟悉”、“一般”、“熟悉”、“很熟悉”四个等级。

设备的维修性是指可修复设备在故障发生后，在规定时间内和规定的维修条件下，使设备恢复到规定功能的能力。它主要由维修难易程度和备件情况两个子因素构成。维修难易程度分为“需操作人员”、“需技术人员”、“进厂维修”、“需特聘专家”四个等级;备件情况分为“标准件”、“自制”、“需特购”和“难以购买”四个等级。

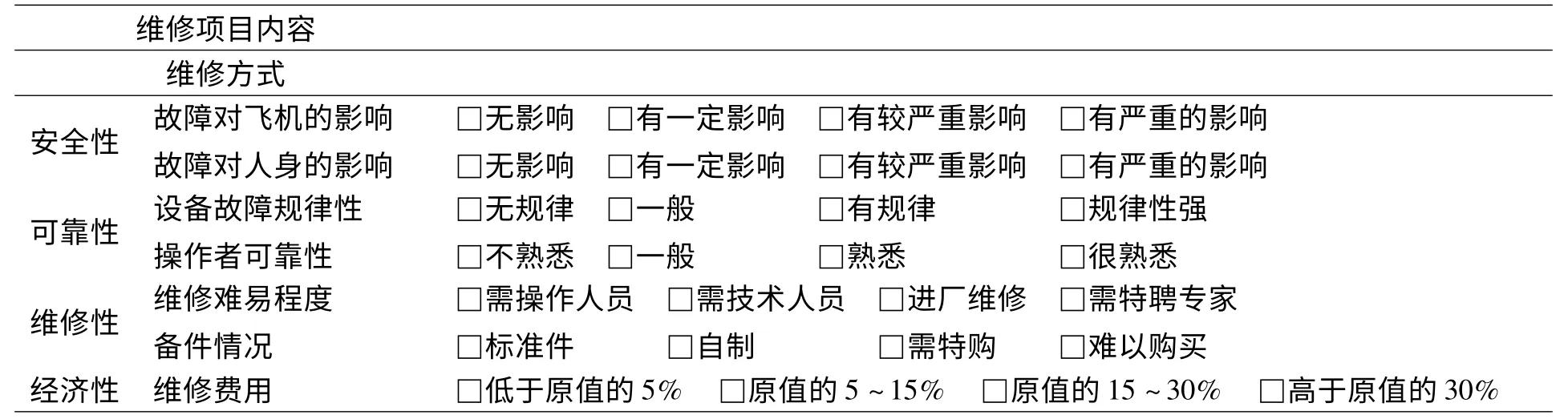
表2 维修方式决策信息外场采集表

经济性主要是指故障的维修费用，分为“低于原值的5%”、“原值的5～15%”、“原值的15～30%”和“高于原值的30%”四个等级。这些维修方式决策信息外场采集表见表2，对于每一项维修工作都填写该表。

2 不完备信息下规则直接获取算法

在粗糙集理论里，约简定义为一个描述所有特征所需的最小属性集。所谓规则约简，就是指能定义对象基本概念的属性子集，它利用一部分条件属性就能够唯一的确定决策值。因此，规则约简实际上就是决策规则。一般的约简算法不能直接产生最小规则，如Pawlak提出的RG算法［9］，这类算法所产生的规则会有重叠，并不能唯一的描述决策规则，还要另外进行相应的规则约简。在数据量大的情况下，这部分工作耗时较多。针对此类不足，Kusiak等人提出的改进RG算法能够直接产生最小约简［10］。它的基本思想是从一阶规则开始，先挖掘低阶规则约简，根据所获取的低阶规则约简对决策表进行相应处理后，再进行高阶规则的挖掘，从而保证规则之间不产生重叠，直接获得最小约简。

根据容差关系对不完备信息的“遗漏值”解释，将不完备信息系统中的遗漏值用M代替，它可以取该属性下可能的任何值。设决策表为T，aij为对象i在第j个条件属性的取值，di为对象i的决策属性值，M表示遗漏值［11］。确定性规则直接获取算法流程如下:

步骤0:根据决策属性值，重新排列决策表T=(U，A，D)。

步骤1:初始化对象i=1，特征约简阶数r=1。

步骤2:从i行，j=1列开始查找。若aij≠＊且aij≠M，则转3，否则转4。

步骤3:对于所有的k≠i，如果aij≠akj≠M，或者aij=akj∧di=dk，或者akj=M∧di=dk，则aij可以用来生成r阶约简。如果所有列j=1，…，n都已被查找，则转4;否则，回到2，从下一列j=j+1开始查找。

步骤4:置i=i+1，回到2，直到所有对象都已被查找。当所有对象都已被查找后，转5。

步骤5:基于有着相同对应特征(条件属性)值的对象，修订决策表T，将用来构成相应1阶特征约简的属性值aij‘x’替换成‘*’，转6。

步骤6:基于调整后的决策表T'，置r=r+1，开始生成高阶约简。若r=m，则停止。否则置i=1，转7。

步骤7:从i行开始寻找r个合适的特征Fj1，…，Fjr和aij1，…，aijr去生成一个r阶特征约简(集合aij1，…，aijr}可以用来生成一个r阶特征约简的条件是，它的所有子集中没有一个被用来生成过低阶的约简或者整个组合没有被标记为已经用来构成一个r约简)。如果这样一个集合aij1，…，aijr存在，转8，否则，转9。

步骤8:对于所有的k≠i，当至少有一个j=j1，…，jr时，有aij≠akj≠M或aij=akj≠M∧di=dk;或akj⊇M且对于所有的jp={j1，…，jr}-jm有aijp=akjp∧di=dk，则{aij1，…，aijr}构成一个r阶特征约简。基于拥有同样相应合适集的对象，每一aij1，…，aijr被同样的符号如“*r”标明其组合{aij1，…，aijr}已经被用来生成一个r阶约简，因此它不能够被用来生成任一更高阶约简的任一部分。转7。

步骤9:置i=i+1，若i＞|U|，回转6，否则回转7。

3 维修方式决策规则粗集获取

3.1 建立决策问题的不完备决策数据表模型

外场在填写信息采集表时，有一些项目可能暂时无法判定选择哪个等级，填写人员当时无法填写，随后也未补上，这样就造成了信息的残缺。比如安全性一项，有些故障对于是否能够造成人员或者飞机的危害无法明确，无法填写。这种情况还将出现在填写设备故障规律、维修费用等项目的时候。某型飞机飞行前的17项预防性维修工作分别进行了这些因素的判断，其维修内容如表3所示。将收集到的数据整理后得到一个不完备的决策表，见表4。

表3 飞行前维修内容

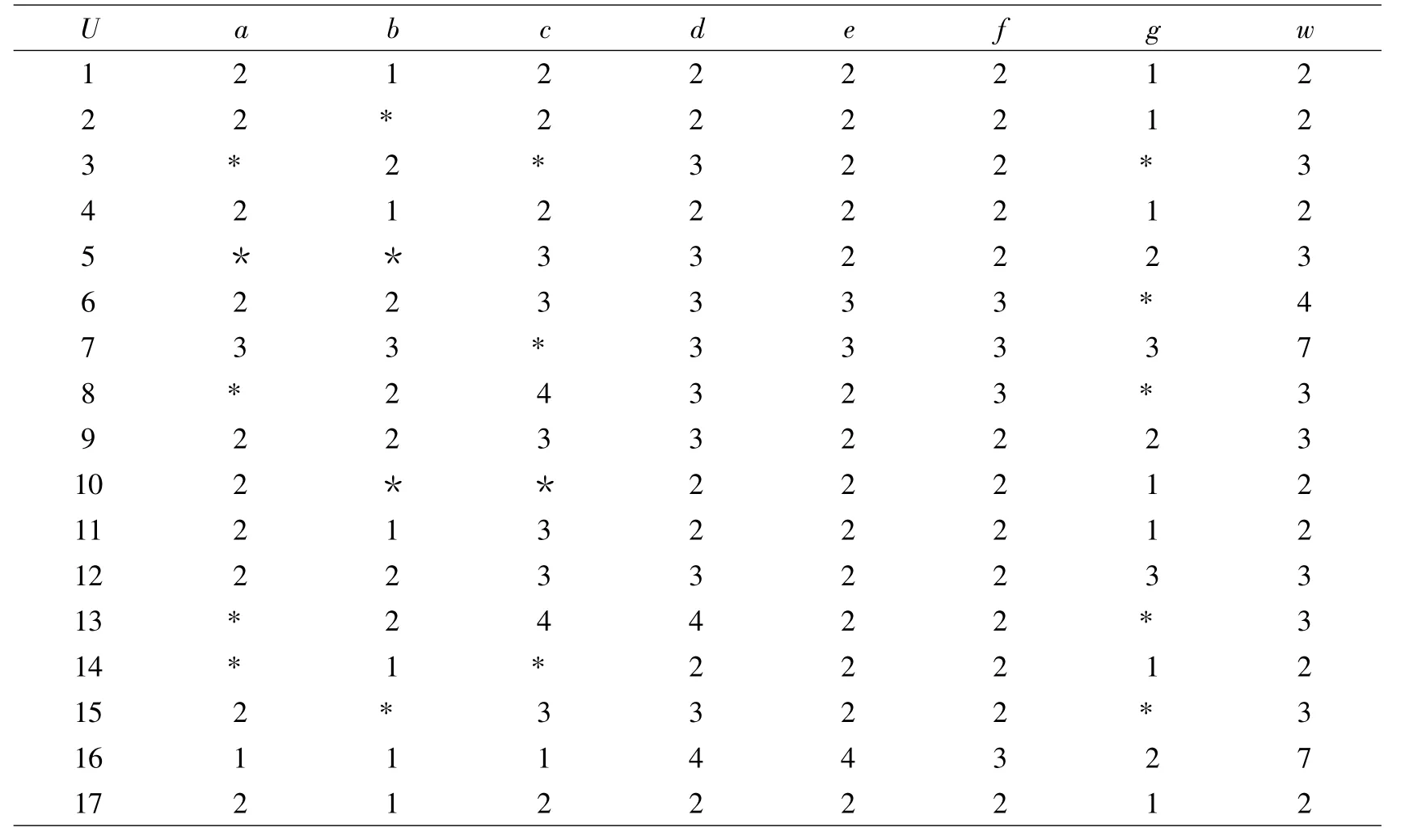
表4 维修方式影响因素信息表

3.2 属性值识别、特征化，连续属性离散化

表中a，b，c，d，e，f，g分别表示表1中各影响因素，表2中每个因素的四个等级分别用1、2、3、4四个数字表示。比如对于故障对飞机本身影响，1表示“无影响”，2表示“有一定影响”，3表示“有较严重影响”，4表示“有严重的影响”。U={1，2，…，17}表示17项维修工作。w为决策属性，代表维修工作所采用的维修方式，用数字1～7分别表示保养、操作人员监控、使用检查、功能检测、定时拆修、定时报废和综合工作维修七种维修方式。

3.3 维修规则获取

按照不完备信息下规则直接获取算法，共生成了29条确定性规则，其中有1条一阶规则，22条二阶规则，6条三阶规则。以综合工作维修方式为例，生成的规则如表5所示，对象数表示该条规则是从多少条记录中得到的，可信度为1表示该条规则为确定性规则。从规则1可以看出，当维修难度很高时，应该采用综合维修方式;从规则2可以看出，当故障对飞机影响较严重，且维修需进场维修时，应该采用综合工作维修方式;从规则11可以看出，当故障对人身安全无影响，故障无规律且维修费用达到原设备费用的5%～15%时，应采用综合工作维修方式。这与综合逻辑决断法得到的结果和实际情况相吻合。所有的决策规则都来自于实际数据，不需要决策者按照逻辑决断图去回答繁琐的问题，方便有效，且更加客观。

表5 综合工作维修方式规则库

4 结束语

将粗糙集的方法应用到维修方式的决策中，通过外场提供的实际维修工作数据，从不完备信息表中直接获取维修方式的决策规则，为客观地确定维修方式规划提供了新的思路和依据。

1 张恒喜.数字化维修理论与技术［M］.北京:国防工业出版社，2006.

2 陈学楚.现代维修理论［M］.北京:国防工业出版社，2003.

3 HU X H，CERCONE N.Discovering Maximal Generalized Decision Rules through Horizontal and Vertical Data Reduction［J］.Computational Intelligence，2001，17(4):685-702.

4 WANG G Y，WU Y，FISHER P S.Rule Generation based on Rough Set Theory［c］//Data Mining and Knowledge Discovery:Theory，Tools，and Technology II，2000.

5 SLOWINSKI K，STEFANOWSKI J，SIWINSKI D.Application of Rule Induction and Rough Sets to Verification of Magnetic Resonance Diagnosis［J］.Fundamental Informatica，2002，53(3-4):345-363.

6 INUIGUCHI M.Generalizations of Rough Sets and Rule Extraction［J］.Lecture Notes in Computer Science，2004，3100:96.

7 孟科.粗集智能决策方法及其在军用飞机型号发展工程中的应用［D］.西安:空军工程大学，2006.

8 HDBK M.Maintenance Evaluation and Program Development［S］.America，1968.

9 PAWLAK Z.Rough sets:Theoretical Aspects of Reasoning about Data［M］.Dordrecht，The Netherlands:Kluwer Academic Publishers，1991:168.

10 KUSIAK A，TSENG T L.Modeling Approach to Data Mining［C］.Glasgow，Scotland，1999.

11 江洋溢.粗糙集不确定分析及在军用飞机型号发展工程中的应用［D］.西安:空军工程大学，2007.