航空兵飞行保障系统效能评估模型研究

2012-12-15熊哲许瑞明潘冠霖陈庆印

军事运筹与系统工程 2012年2期

关键词：保障系统服务台可信性

熊哲，许瑞明，潘冠霖，陈庆印

(军事科学院军事运筹分析研究所，北京100091)

1 引言

航空兵飞行保障系统效能的高低直接关系到航空兵部队是否能够及时、有效地完成各项任务。对航空兵飞行保障系统效能进行评估，便于充分了解飞行保障能力，深入认识飞行保障现状中存在的问题，为指挥员做好飞行保障工作提供决策依据。

目前，针对航空兵飞行保障系统效能的评估存在以下问题:

一是就评估方法而言，大多停留在局部的、静态的、定性的评估，甚至依靠经验的判断。

二是以往的方法是将航空兵飞行保障系统分解为若干个子系统，以子系统的效能评估结果为依据，进行综合加权求和得出飞行保障系统效能，没有考虑到子系统之间的不可替代性。

三是对系统能力的评估，通常采用的是专家打分等分析手段，主现因素较多。

本文以效能评估ADC方法为基本框架，通过分析航空兵飞行保障系统的各个子系统，以及确定子系统的可用性、可信性和能力3个因素，构建基于ADC方法的飞行保障系统效能评估模型，为飞行保障的组织指挥和系统建设提供决策依据。

2 航空兵飞行保障系统效能分析结构模型

航空兵飞行保障系统是一个复杂的随机服务系统，系统完成任务的概率是系统效能最主要的指标。飞行保障系统在开始执行任务的状态用系统的“可用性”来描述，在执行任务过程中的状态用系统的“可信性”来描述，在系统处于可用及可信状态下，系统完成任务的程度则用系统的“能力”来描述。

由于航空兵飞行保障系统具有递阶的层次结构，可以将其逐级的分解为若干分系统和子系统，并且居于底层的子系统之间存在不可替代性。因此，飞行保障系统的可用性、可信性、“能力”可以用底层的子系统的可用性、可信性、“能力”来描述。

飞行保障系统效能分析结构模型如图1所示。

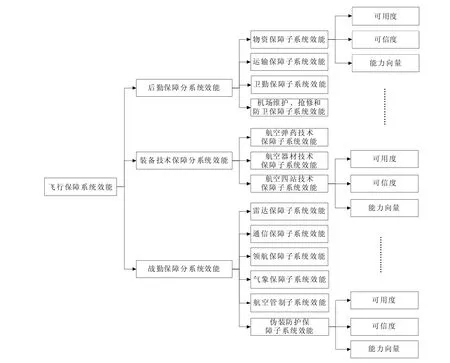
图1 飞行保障系统效能分析结构模型

3 航空兵飞行保障系统效能评估模型

按照航空兵飞行保障系统效能的结构模型，逐一确定系统的可用性向量、可信性矩阵以及能力矩阵。

3.1 可用性向量

可用性向量A是由系统处于开始阶段中所有可能状态的概率组成，一般表达式为:A=［a1，a2，…，an］。其中ai(i=1，2，…，n)是不同状态的概率，n种可能状态构成了n维向量空间。飞行保障系统开始执行任务时的状态可划分为正常状态和发生故障状态，则系统的可用性向量为:A=［a1，a2］。式中:a1、a2分别表示系统在开始执行任务时处于正常、发生故障状态的概率(即不可用度)。

航空兵飞行保障系统中的各个分系统和子系统均是由不同类型的保障装备组成。就保障功能而言，不同类型的保障装备形成一个串联系统，而同类型的保障装备之间则构成一个并联系统，如图2所示。

图2 飞行保障系统要素的构成

以装备技术保障分系统中的航空四站技术保障子系统为例，设该子系统中的第i个类型装备(例如充氧车)的故障率、修复率及其数量分别为λi、μi和ni。则根据可靠性理论，单个第i类型装备的可用度计算公式为:

其中，MTBF为平均故障间隔时间，MTTR为平均修复时间。则航空四站技术保障子系统中所有第i个类型装备并联后的可用度为:=1--aj)。

设航空四站技术保障子系统中共有m种不同类型的保障装备，则航空四站技术保障子系统的可用度向量为:

同理，可得到其他子系统的可用度向量。

3.2 可信性矩阵

可信性矩阵D是由系统的各种状态变化为其他状态的概率组成，仍以航空四站技术保障子系统为例，若子系统开始执行任务时有种可能状态，则在执行任务过程中可能呈现n×n种系统状态转移情况。因此，可信性是一个n×n阶的矩阵，即:

式(1)中，dij表示已知子系统在开始执行任务时处于第i种状态，而执行任务的过程中处于第j种状态的概率，称之为系统的转移概率。

将航空四站技术保障子系统在执行任务中的状态划分为“正常工作”和“发生故障”两种状态，则可信性矩阵为:

式(2)中，d11、d12分别表示航空四站技术保障子系统在开始执行任务时处于正常工作状态，在执行任务过程中处于正常工作状态和故障状态的概率;d21、d22则分别表示子系统在开始执行任务时处于故障状态，在执行任务过程中处于故障状态和正常工作状态的概率。则d12=1-d11，d22=1-d21。故有:

同理，可得到其他子系统的可信性矩阵。

3.3 能力矩阵

能力矩阵(cjk)m×n表示系统在各个可用状态下的能力，是指已知系统执行任务过程所处状态条件下达到任务目标的能力。航空兵飞行保障系统下的子系统在执行飞行保障任务过程中仅有工作和不工作两种模式，因此能力矩阵仅有c1、c2两个向量，又因为系统处于故障状态时，无法完成任务，所以有c2=0，能力矩阵如公式(4)所示:

根据飞行保障系统的保障特性，可通过设定各个子系统在规定时间内可保障飞机架次的最大期望值和最小期望值来衡量各个子系统的能力，见公式(5)。

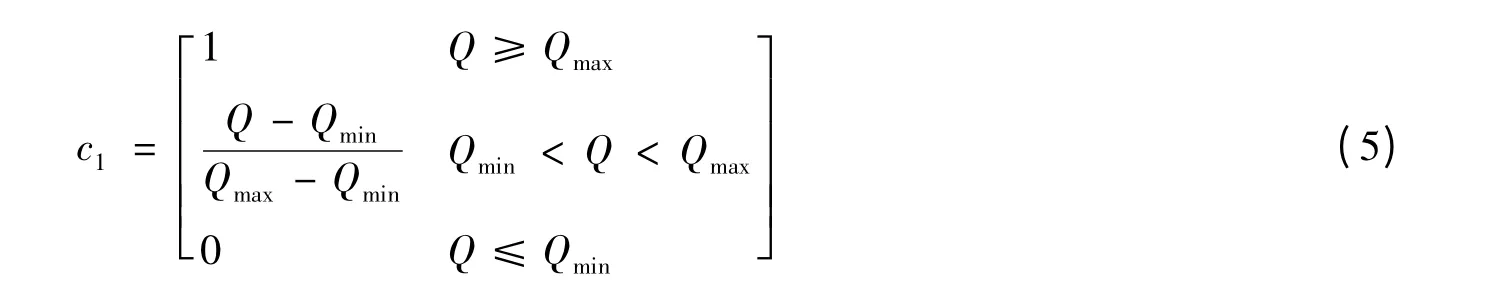
式(5)中，Q为子系统在任务执行时间内保障飞机的架次，Qmax、Qmin分别为子系统在任务时间内保障飞机架次的最大期望值和最小期望值。Q值通过排队论模型求解。

子系统均可看作为由顾客源有限的等待制的多个多服务台的排队系统构成。例如，航空四站技术保障子系统就包括了由电源车、充氧车、充氮车、加油车构成的4个多服务台排队系统。

首先，考虑子系统中单个多服务台排队系统的情况，设飞机到达的间隔时间和服务时间分别服从均值为的负指数分布，服务规则是先到先服务。m为需要保障的飞机数量(顾客数量)，n为某类型保障装备的数量(服务台数量)。设ρ=，该多服务台排队系统空闲的概率为:

顾客有效的到达率αe(即每架飞机的到达率乘以其在子系统外的期望数):αe=α(m-Ls)

顾客(飞机)在多服务台排队系统中的平均逗留时间为:Ws=

则该多服务台排队系统在任务执行时间内的保障飞机架次为:Qi=

其中，T为任务执行时间，Qi表示航空四站技术保障子系统中由第i类装备组成的多服务台排队系统，在规定任务执行时间内的保障飞机架次。

由于航空兵飞行保障系统中的各个子系统中均包含多种不同类型的保障装备(如电源车、充氧车等)，因此，可将其视为由多个不同类型的多服务台排队系统所构成，而多个多服务台排队系统之间并不是简单的串、并联关系(例如，当飞机从由充氧车构成的多服务台排队系统中退出后，可随机进入此时空闲的由加油车、充氮车等其他多服务台排队系统)，因此，航空四站技术保障子系统的在任务执行时间内保障的飞机架次取决于保障飞机架次最小的多服务台排队系统，即Q=min{Q1，Q2，…，Qk}。其中，k为子系统中包括的多服务台排队系统的个数，即子系统中包括的保障装备类型数量。

最后，通过设定子系统在规定任务执行时间内可保障飞机架次的最大期望值和最小期望值，以及公式(4)和(5)即可求得该子系统的能力向量。

3.4 飞行保障系统效能评估综合模型

由于航空兵飞行保障系统的后勤保障分系统、装备技术保障分系统以及战勤保障分系统之间具有不可替代性，且分系统下的子系统之间也均具有不可替代性。因此综合上述，可得到航空兵飞行保障系统效能的综合值为:

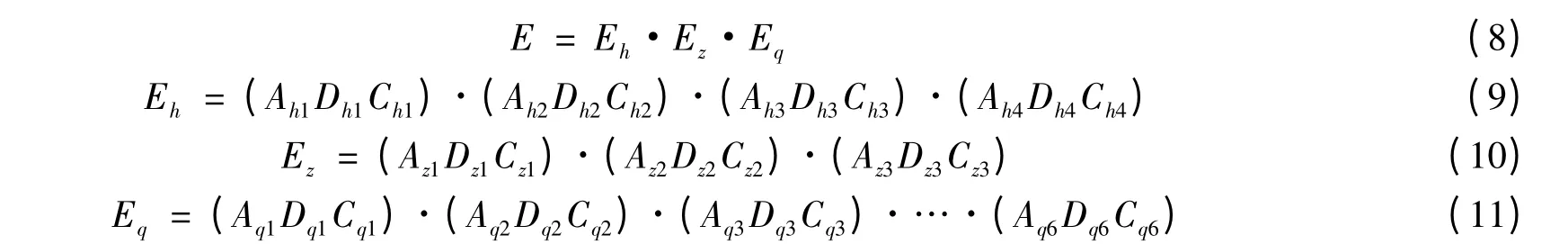
其中，Eh、Ez、Eq分别表示后勤保障、装备技术保障和战勤保障分系统的效能值;Ah1，Ah2，…，Ah4分别表示后勤保障分系统中物资保障、运输保障等子系统的可用性向量;Az1，Az2，Az3分别表示装备技术保障分系统中航空弹药技术保障、航空器材技术保障等子系统的可用性向量;Aq1，Aq2，…，Aq6分别表示战勤保障分系统中雷达保障、通信保障等子系统的可用性向量。可信性向量与能力矩阵表示方法同上。

4 实例分析

设某航空兵飞行保障系统的航空四站技术保障子系统中现有的电源车、充氧车、充氮车、加油车的MTBF、MTTR参数值和数量见表1。

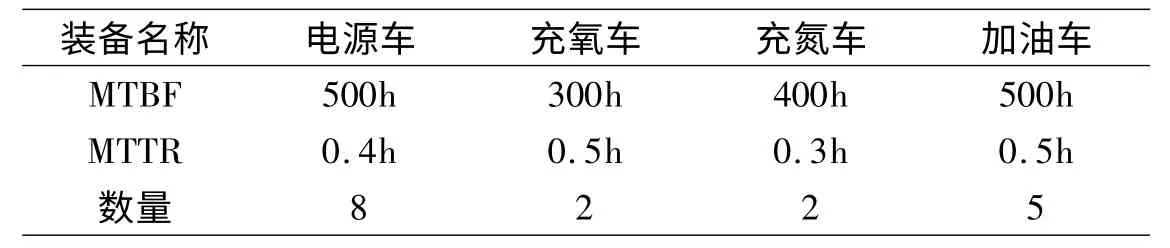
表1 航空四站技术保障子系统装备参数值

设任务执行时间为5H，保障某型飞机10架，飞机到达率为α=0.2架/分钟，电源车、充氧车、充氮车、加油车的服务时间分别为β1=10分钟/架、β2=8分钟/架、β3=5分钟/架、β4=15分钟/架，并将保障飞机架次的最大期望值和最小期望值分别设置为95架次和65架次。可求解得到该航空四站技术装备保障子系统的可用性向量为:Az3=［0.87，0.13］。可信性矩阵为能力向量为:Cz3=［0.912，0］T。则航空四站技术装备保障子系统的效能值为:Ez3=Az3Dz3Cz3=0.77。以此类推，分别求解航空弹药技术保障子系统、航空器材技术保障子系统的效能值分别为0.82和0.91，则该飞行保障系统的装备技术保障分系统的效能值Ez=0.77×0.82×0.91=0.57，同理可得，后勤保障分系统和战勤保障分系统的效能值为Eh=0.87，Eq=0.92，故该飞行保障系统的效能值E=0.57×0.87×0.92=0.46。