Banach空间中一类广义向量变分不等式解的存在性

张 艳,何中全,阿力非日

(西华师范大学数学与信息学院,四川南充637009)

向量变分不等式是变分不等式的推广形式,最早于1980年由Giannessi[1]在有限维欧式空间中引入和研究。随后,许多学者研究了向量变分不等式,向量变分不等式在无限维空间中得到广泛研究和推广[2,3]。受文献[1,2,4-6]的启发,本文引入一类具有更一般形式的广义向量变分不等式,并通过KKM定理证明其解的存在性及解的一些性质。

1 预备知识

设X,Y为实的Banach空间,L(X,Y)为X到Y的有界算子的全体,K⊂X为非空闭凸子集,〈t,x〉为t在x处的值,t∈L(X,Y),x∈X,2L(X,Y)为L(X,Y)的非空子集全体,C:K→2Y为非空闭凸点锥集值映射,且∀x∈K,C(x)是Y中的真闭凸锥,int C(x)≠φ,{C(x)}∩{-C(x)}={0}。设f:KXK→Y, A,T:K→L(X,Y),N:L(X,Y)XL(X,Y)→2L(X,Y),η:KXK→K是5个映射。

考虑下面的广义向量变分不等式问题GVVIP:求x*∈K,∀y∈K,∃sy∈N(Ax*,Tx*)使得

特殊情况:

(1)如果A≡I,T≡I,N(x,x)=F(x),则问题GVVIP转化为下面的向量变分不等式问题VVIP:求x*∈K使得

此问题在文献[1]中被引入和研究。

(2)如果f(y,x)=f(y)-f(x),则问题VVIP转化为:求x*∈K使得

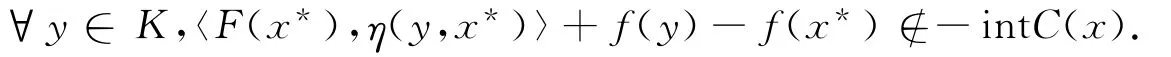
在文献[6]中,Irfan和Ahmad利用KKM定理和逃逸序列的方法研究了该向量变分不等式解的存在性。为了得到本文的结果,需要下面的定义和引理。

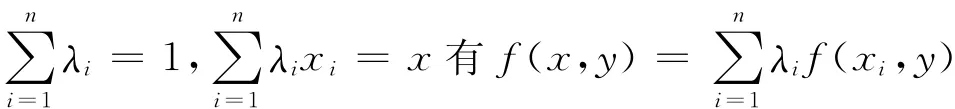
定义2[7](KKM映射) 设E是一线性空间,K是E的一非空子集,G:F→2E是一多值映射。称G为 KKM映射,如果对任一有限集{x1,x2,…,xn}⊂K,有co{x1,x2,…,xn}⊂G(xi),其中co{x1,x2,…,xn}表示{x1,x2,…,xn}的凸包。

定义3[4]设X,Y为两个拓扑空间,F:X→2Y是一集值映射。

(1)如果对包含F(x)的每一个开集V⊆Y,存在包含x的开集U,∀t∈U,F(t)⊆V,则称F在x∈X点为上半连续;如果F在X上每一点上半连续,则称F在X上上半连续。

(2)如果对每一个开集V⊆Y且F(x)∩V≠φ,存在包含x的开集U,∀t∈U,F(t)∩V≠φ,则称F在x∈X点为下半连续;如果F在X上每一点下半连续,则称F在X上下半连续。

(3)如果F的图,即Gr(F)={(x,y)∈XXY|y∈F(x)}是XXY的闭子集,则称F为闭映射。

引理1[5]设(V,P)是一有序的Banach空间,P是V中之一闭的尖凸锥,且int P≠φ,则对任意的x, y,z∈V有

(1)如果x-y∈-int P(x),且x∉-int P(x),则y∉-int P(x);

(2)如果x+y∈P(x),且x+z∉-int P(x),则z-y∉-int P(x);

(3)如果x+z-y∉-int P(x),且-y∈-P(x),则x+z∉-int P(x);

(4)如果x+y∉-int P(x),且y-z∈-P(x),则x+z∉-int P(x)。

引理2[7](Fan-KKM定理) 设E是一Hausdorf线性拓扑空间,F是E中的非空子集,G:F→2E为一KKM映射,对每一个x∈F,G(x)为E中的闭集,且至少存在一点x0∈F,使G(x0)是E中的紧集,则G(x)≠φ。

引理3[4]设X,Y为两个拓扑空间,F:X→2Y是一集值映射,那么以下结论成立:

(1)如果F是紧值的,则F在x∈X点为上半连续当且仅当对任意网{xα}⊆X且xα→x,对任意网{yα}⊆Y且yα∈F(xα),存在y∈F(x)以及{yα}的子网{yβ},使得yβ→y。

(2)F在x∈X点为下半连续当且仅当对任意y∈F(x)以及任意网{xα}⊆X且xα→x,存在{yα}⊆Y且yα∈F(xα),使得yα→y。

(3)F是闭映射当且仅当对任意网{xα}⊆X且xα→x,对任意网{yα}⊆Y,yα∈F(xα)且yα→y,则y∈F(x)。

2 主要结果与证明

定理1 设X,Y为实的Banach空间,L(X,Y)为X到Y的有界算子的全体,K⊂X为非空闭凸子集。设C:K→2Y为非空闭凸点锥集值映射,∀x∈K,C(x)是Y中的真闭凸锥且int C(x)≠φ,{C(x)}∩{-C(x)}={0}。给定映射A,T:K→L(X,Y),f:KXK→Y,N:L(X,Y)XL(X,Y)→2L(X,Y),η:KXK→K,假设下面的条件成立:

(a)f,A,T,η连续,且x→N(Ax,Tx)下半连续;

(b)集值映射W:K→2Y定义为∀x∈K,W(x)=Y{-int C(x)}是闭映射;

(c)存在映象h:KXK→Y,使得

(i)∀x∈K,h(x,x)∈C(x),

(ii)对∀x,y∈K,∃sy∈N(Ax,Tx),使得〈sy,η(y,x)〉+f(y,x)-h(x,y)∉-int C(x),

(iii)∀x∈K,{y∈K|h(x,y)∉C(x)}凸;

(d)存在K的非空紧凸子集D,使得对∀x∈KD,∃y∈D,有

则广义向量变分不等式GVVIP有解,且其解集为紧集。

证 定义集值映射G:K→2D,∀y∈K,

(1)首先证明对∀y∈K,G(y)是D中的闭集。

事实上,设{xα}⊆G(y)且xα→x0,由于{xα}⊆D且D为紧集,故x0∈K。由于N是下半连续的,由引理3(3)知,对∀y∈K,∃s0y∈N(Ax0,Tx0),对∀α,∀y∈K,∃sαy∈N(Axα,Txα)满足序列{sαy}→{s0y}∈L(X,Y)。由于对∀α,xα∈G(y)有,∀y∈K,∃sαy∈N(Axα,Txα),使得