弯曲载荷下隔水管特殊螺纹接头参数与应力关系研究

刘贤玉，于永南，宋作苓，孙建忠

（中国石油大学储运与建筑工程学院，山东青岛266555） ＊

弯曲载荷下隔水管特殊螺纹接头参数与应力关系研究

刘贤玉，于永南，宋作苓，孙建忠

（中国石油大学储运与建筑工程学院，山东青岛266555）＊

针对海洋环境中隔水管存在较大弯曲载荷的情况，采用有限元软件ANSYS对隔水管最易失效的特殊螺纹接头建立了三维接触有限元模型，得到了在弯曲载荷作用下螺纹接头的应力分布。结果表明：最大应力出现在接头本体拉伸侧的第1圈或最后1圈螺纹的根部；接头本体拉伸侧与压缩侧的螺纹根部应力分别与环向角近似成1／2个正弦波函数关系。在此基础上进一步分析了壁厚、螺高、螺距、螺纹圈数和锥度等参数对螺纹处最大等效应力的影响，为隔水管特殊螺纹接头的设计与优化提供了理论依据。

隔水管；弯曲载荷；特殊螺纹；应力；ANSYS

隔水管是避免海上油井发生事故的主要工艺结构之一。由于隔水管特殊螺纹接头可以极大地提高生产效率，降低生产成本，因此特殊螺纹接头隔水管得到了较广泛的应用。隔水管处于较复杂的海洋环境中，在风、海浪以及海流等作用下，隔水管承受弯曲、轴力、外压、内压等多种载荷，工作条件恶劣，因而易出现隔水管失效事故。导致隔水管失效的主要载荷是弯曲载荷，隔水管特殊螺纹连接处是最薄弱环节。目前对螺纹连接的研究主要集中在上扣、内压、外压与轴向载荷等对称边界与载荷，并简化成平面模型求解［1－4］。隔水管螺纹接头承受的弯曲载荷为非轴对称载荷，较难简化成平面轴对称模型求解［5－6］。目前尚未发现通过建立三维有限元模型，对弯曲载荷作用下特殊螺纹接头应力分布规律进行研究的文献报道。为提高隔水管螺纹的连接强度，避免螺纹过早失效，本文利用ANSYS软件建立了特殊螺纹接头三维简化模型，分析了螺纹接头在弯曲荷载作用下螺纹处应力分布规律，进而分析了应力与螺纹参数之间的关系［7－9］，为隔水管特殊螺纹的设计优化提供依据。

1 接头模型与边界条件

以东海某油田609.6mm×25.4mm（24英寸×1英寸）隔水管为例，在百年一遇波流作用下，隔水管最大弯矩为1 974kN·m，相应的轴向拉力为243.6kN。由于隔水管承受的弯矩较大，将隔水管特殊螺纹接头设计成偏梯形螺纹连接［10］，导向侧面与螺纹轴线的垂线间的夹角为10°，承载面与螺纹轴线的垂线间的夹角为3°。3°承载面可使螺纹在较大的轴向拉伸载荷下具有抗滑脱性能，而10°导向面可使螺纹承受较大的轴向压缩载荷［11］。

螺纹连接处的接触面为空间螺旋面，但由于螺纹升角较小，故建模时忽略升角影响，将结构视为轴对称结构。螺纹接头建模采用三维20节点等参单元solid95，此单元可用来模拟不规则形状而不会降低精度。利用接触向导生成接触对，目标单元采用Targe170，接触单元采用Contact174，摩擦因数取0.2。由于应力集中主要在螺纹啮合处［2］，故在建模时对螺纹连接处进行网格细化，其余部位进行较粗的网格划分。材料模型采用线弹性材料模型，弹性模量210GPa，泊松比0.3。对内螺纹远离螺纹牙处的端面全约束，外螺纹远离螺纹牙处的端面施加弯矩1 974kN·m，拉力243.6kN，其有限元模型如图1所示。

图1 有限元计算模型

为了便于计算结果的处理，对接头的螺纹牙进行编号。螺纹牙号以内螺纹为标准，从内螺纹的挡肩面开始为螺纹牙第1圈，外螺纹牙圈号与内螺纹对应。

2 有限元分析结果

隔水管螺纹锥度为1︰16，螺高h为7mm，螺距P为30mm，圈数n为7，接头最大总厚度为85.4 mm，经有限元计算得外螺纹等效应力分布如图2所示，内螺纹应力布如图3所示。由图2～3可知：在弯曲与轴向拉伸载荷作用下，接头应力分布不均匀，螺纹处及管体连接处应力集中明显；接头等效应力（Von Mises应力）最大值为477MPa，发生在外螺纹本体拉伸侧最后1圈螺纹根部；内螺纹等效应力最大值为364MPa，发生在内螺纹本体拉伸侧第1圈螺纹根部。

图2 内螺纹等效应力云图

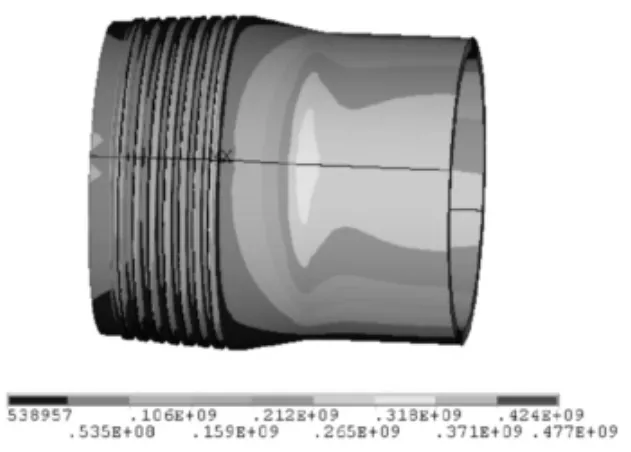
图3 外螺纹等效应力云图

各圈螺纹的最大等效应力与法向最大接触压力分布曲线如图4所示。由图4可知：螺纹牙接触压力两端较大，中间较小，且最后2圈的接触压力较前2圈的接触压力大，最大接触压力均发生齿腹部分；外螺纹前2圈等效应力相对较小，后5圈应力随着圈号的增加而逐渐增大；内螺纹两端螺纹应力较大，中间螺纹应力较小，螺纹应力随圈号近似呈抛物线分布；内外螺纹每圈最大应力均发生在接头本体拉伸侧的齿根部位，数值上每圈螺纹的最大应力均明显大于最大接触压力。

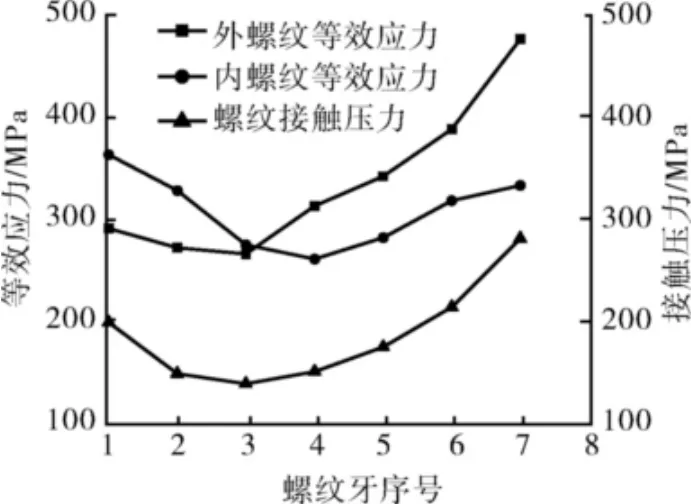
图4 各圈螺纹牙最大等效应力及接触压力

螺纹局部等效应力与接触压力分布曲线如图5所示，其中环向角0～180°对应在弯曲载荷下接头本体拉伸侧的螺纹，环向角180～360°对应接头本体压缩侧的螺纹。在接头本体拉伸侧，内螺纹挡肩与外螺纹靠近螺纹牙处的端面相分离，无接触压力；在接头本体压缩侧，挡肩接触压力分布与环向角近似成1／2个正弦波函数关系，接触压力最大值为105MPa。接头本体拉伸侧与压缩侧的螺纹牙应力及接触压力分布分别与环向角近似成1／2个正弦波函数关系。由于接头本体压缩侧的挡肩承受了较大的接触压力，故同一圈螺纹在接头本体压缩侧的接触压力及应力远小于拉伸侧对应位置处的接触压力与应力。

图5 外螺纹局部等效应力及接触压力

3 螺纹参数的影响

3.1 螺纹壁厚

螺纹最大等效应力随螺纹接头处总壁厚的变化曲线如图6所示。各圈螺纹牙接触压力分布与螺纹本体的刚度和螺纹牙的刚度有关，螺纹本体刚度越大，螺纹牙刚度越小，则各圈螺纹牙承受的接触压力越均匀，螺纹最大应力越小［12］。当螺纹接头总壁厚增加时，螺纹本体刚度变大，从而使各螺纹牙应力分布趋于均匀，螺纹最大应力降低。当螺纹壁厚增加到一定值时，螺纹啮合处相对管体位置出现了较明显的偏移，使螺纹应力分布不均匀，最大应力不再减小甚至增加。

图6 不同加厚厚度螺纹等效应力

3.2 螺高

螺纹最大等效应力随螺高的变化曲线如图7所示。一方面，螺高增加时螺纹牙柔性增大，从而使螺纹接触压力分布较均匀，同时螺高的增加使得螺纹接触区域增大，使接触压力分布更为合理，各螺牙应力较为均匀；另一方面，在相同大小的接触压力下，螺高较大时螺纹牙的根部应力相对螺高较小时的根部应力大，增加螺高，会加剧螺纹根部应力集中。当螺高较小时，增加螺高可明显改善接触压力分布，而螺纹根部应力集中还不太显著，故螺纹最大应力减小。螺高增加到一定值时，螺纹牙较大的柔性使得每圈螺纹承受的总接触压力相近；继续增加螺高，每圈螺纹的总接触压力变化不大，而较大的螺高使得螺纹牙根部应力集中明显，螺纹最大应力增加。当螺距为20、25、30mm时，螺纹最大应力在螺高为5 mm时取最小值；螺距为35mm时，螺纹最大应力在螺高为6mm时取最小值。

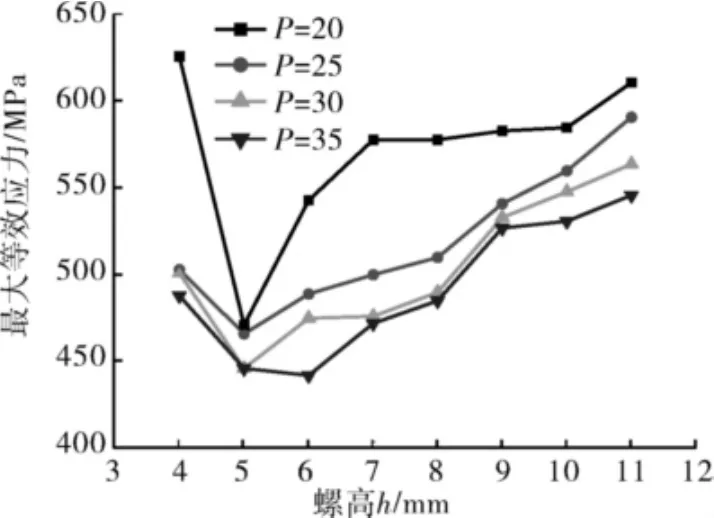
图7 不同螺高螺纹等效应力

3.3 螺距

螺纹最大等效应力与螺距的变化曲线如图8所示。由图8可知：随着螺距的增大，最大等效应力减小。一方面，螺距的增加提高了单圈螺纹牙的抗弯刚度与抗剪强度，提高了单圈螺纹牙承载能力，螺纹根部应力减小；另一方面，螺纹牙刚度的增加会使螺纹接触压力分布不均匀，尤其是螺纹第1圈与最后1圈啮合处（接头高应力区）接触压力明显增大，导致螺纹根部应力增加。当螺距＜35mm时，第1种因素起主导作用，螺距增加时最大应力减小较为明显；当螺距增加为35mm时，2种因素作用基本相当，最大应力基本维持在一定水平内。考虑到螺纹牙的抗剪强度，应在一定范围内增大螺距。

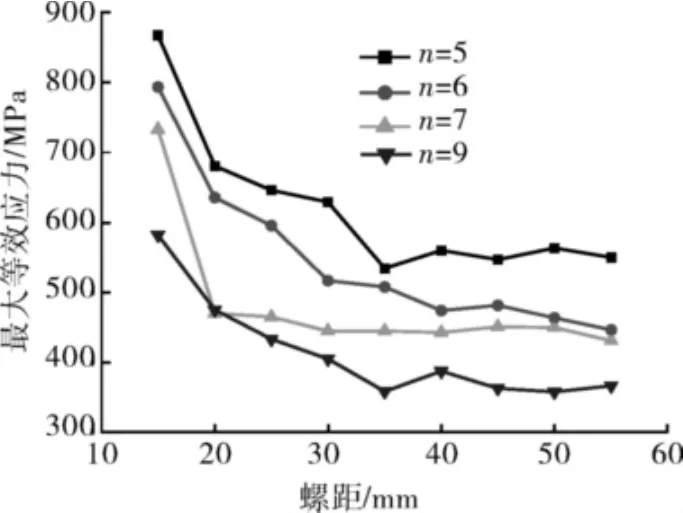
图8 不同螺距螺纹等效应力

3.4 螺纹圈数

螺纹最大等效应力随螺纹圈数的变化曲线如图9所示。随着啮合圈数的增加，螺纹连接处的接触面积增加，单圈螺纹牙承受的接触压力减小，齿根处的应力减小。当圈数n＜7时，螺纹第1圈与最后1圈啮合处接触压力随圈数的增加明显减小，齿根应力较多地转移到了其他螺纹牙上，最大应力降低较显著；当圈数n＞7时，螺纹第1圈与最后1圈啮合处接触压力随圈数的增加降幅不大，最大应力减小较慢，且此时不同螺距下螺纹最大应力相差不大。故隔水管接头螺纹啮合圈数达到一定数目时，再增加啮合圈数并不能显著提高其抗弯强度。

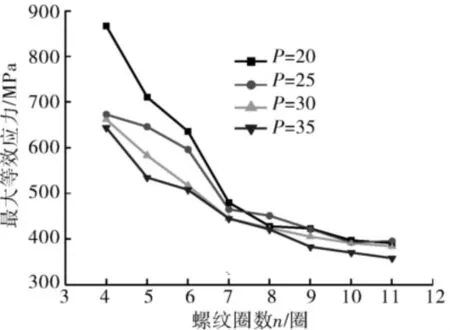
图9 不同螺纹圈数螺纹等效应力

3.5 螺纹锥度

螺纹最大等效应力随螺纹锥度的变化曲线如图10所示。由图10可知：当螺纹锥度从零增大到1︰32时，不同螺纹圈数下的螺纹应力均有较为明显的减小。当螺纹圈数n＜9时，1︰32、1︰16与1︰8锥度下的螺纹应力接近，应力随锥度的增大略有减小；当螺纹圈数n＞9时，螺纹应力随锥度的增大有一定幅度的减小。总体上看，圆锥螺纹锥度的大小对螺纹应力影响不大；圆锥螺纹的应力分布优于柱形螺纹。由于圆锥螺纹的锥度增加了螺纹连接的接触面积与螺纹根部端面积，提高了螺纹连接的定心精度与连接刚性，使得螺纹应力分布较均匀。

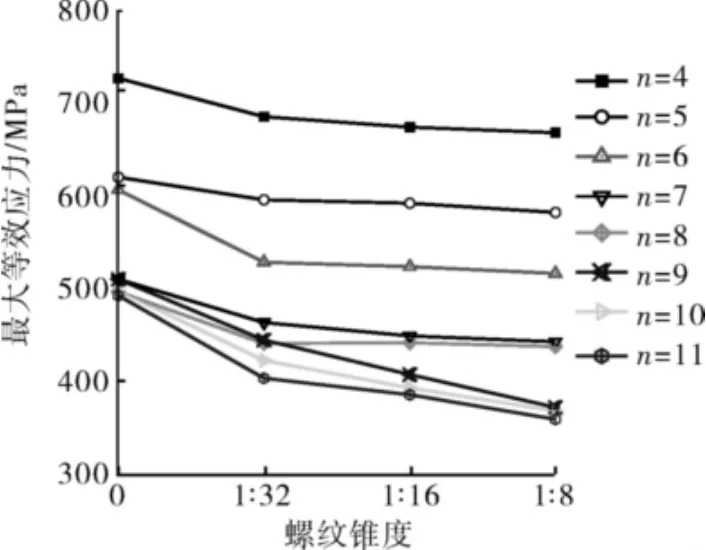
图10 不同螺纹锥度螺纹等效应力

4 结论

1） 各种螺纹参数下接头最大等效应力均出现在接头本体拉伸侧内螺纹第1圈螺纹或外螺纹最后1圈螺纹的根部，该处为应力严重集中区。

2） 在接头本体拉伸侧与压缩侧的接触压力及应力分别与环向角近似成1／2个正弦波函数关系分布，且由于挡肩作用，拉伸侧的应力远大于压缩侧的应力。

3） 增加螺纹壁厚可减小螺纹应力，但壁厚过大反而会使应力增加；螺纹应力随螺高的增大先减小后增大；应力随螺距的增大而减小，螺距增加到一定值时应力变化不大；应力随螺纹圈数的增加而减小，减小幅度先大后小；锥螺纹的应力分布优于柱螺纹，锥螺纹锥度的大小对应力影响不大。

4） 对于本文给定的隔水管尺寸及载荷，综合考虑安全因素与加工成本，螺纹接头取壁厚约80 mm、螺高5～6mm、螺距约30mm、螺纹圈数7左右、锥度1︰16时较为合理。

［1］ 奚杰峰，张春婉，马新沛.钻铤螺纹接头上卸扣过程力学分析［J］.石油矿场机械，2011，40（11）：54－57.

［2］ 王新虎，申照煕，王建东，等.特殊螺纹油管与套管的上扣扭矩构成与密封性能研究［J］.石油矿场机械，2010，39（12）：45－50.

［3］ 王 杰，周永丽，焦 锋，等.油井钢管圆螺纹接头机紧状态下的力学分析［J］.石油矿场机械，2010，39（12）：7－10.

［4］ 何牛仔，高学仕，李兆勇.热采井套管螺纹连接有限元分析［J］.石油矿场机械，2007，36（9）：64－66.

［5］ 林元华，施太和，姚振强，等.钻具螺纹接头力学性能计算方法及其应用［J］.上海交通大学学报，2005，39（7）：1 058－1 062.

［6］ 吴稀勇，闫 龙，陈 涛，等.弯曲载荷下特殊螺纹接头密封性能的有限元研究［J］.计算机研究与应用，2010，39（6）：70－73.

［7］ 张 林，罗 增，林元华，等.双台肩螺纹接头参数与应力应变关系研究［J］.石油矿场机械，2010，39（4）：21－23.

［8］ 申昭煕，李 磊，王 鹏.特殊螺纹接头主要参数对密封性能的影响分析［J］.石油矿场机械，2011，40（1）：38－41.

［9］ 申昭熙，王 鹏，李 磊，等.特殊螺纹接头密封可靠性数值分析［J］.石油矿场机械，2012，41（1）：10－13.

［10］ 李新勇.螺纹实用手册［K］.北京：机械工业出版社，2009.

［11］ 姬丙寅，吕拴录，张 宏.非API规格偏梯形螺纹接头套管连接强度计算［J］.石油矿场机械，2011，40（2）：58－62.

［12］ 卜 炎.螺纹联接设计与计算［M］.北京：高等教育出版社，1995.

Research on Relations of Stress and Parameter of Premium Threaded Connections on Riser Subjected to Bending Load

LIU Xian－yu，YU Yong－nan，SONG Zuo－ling，SUN Jian－zhong
（College of Pipeline and Civil Engineering，China University of Petroleum，Qingdao 266555，China）

According to the situation of riser subjected to large bending load at the ocean circumstance，the 3Dcontact finite element analysis model for premium threaded connections which is the most likely to become failure is established with the finite element software of ANSYS.The characteristic of Stress distribution on threaded connections under bending loads is obtained.The result reveals that the maximum stress exists on the first or the last round of thread root in the tensile side of connections；the relations of thread root stress distribution in the tensile side and compressive side of the connections with circular angle is represented as approximately half sine respectively.On this basis，detailed analysis is given on the effect of the threaded parameter such as wall thickness，depth of thread，thread pitch，number of thread teeth and taper on the maximum equivalent stress.Thus it can be taken as references in design and optimization of premium threaded connections.

riser；bending load；premium threaded；stress；ANSYS

1001－3482（2012）07－0006－05

TE953

A

2012－01－12

刘贤玉（1987－），男，江西九江人，硕士研究生，主要从事管柱力学研究，E－mail：liuxianyu1987＠163.com。