整体最小二乘线性回归模型与算法

丁士俊，姜卫平，杨颜梅

(1．武汉大学测绘学院，湖北武汉430079;2．国家测绘地理信息局精密工程测量与工业测量重点实验室，湖北武汉430079;3．武汉大学卫星导航定位系统技术研究中心，湖北武汉430079;4．陕西测绘地理信息局，陕西西安710000)

一、引 言

整体最小二乘问题首先由G．H．Golub和L．C．F．Van 提出[1]，十多年来，人们对整体最小二乘TLS(total least squares)的算法、解的条件，以及整体最小二乘与最小二乘之间的关系作了许多理论研究[2]。对于一些实际应用问题而言，如信号处理、统计计算、回归分析等都可以归结为对整体最小二乘问题的处理。在勘察测绘科学技术领域中，回归分析方法是一种处理测量数据常用的方法，回归分析模型的传统解法是认为自变量x没有误差，因变量y为具有偶然误差的观测量，应用最小二乘原理，得到回归参数的最佳估值[3]。对于一组测量数据(xi，yi)，i=1，2，…，n，如果在同时考虑观测数据 xi与yi的误差的前提下，求解回归参数的方法属于整体最小二乘回归分析问题。文献[4-8]对该问题进行一些相应的研究;文献[4]与文献[5]分别从两种不同的平差方法进行了讨论;文献[7]对文献[4-5]存在问题进行了分析比较，但对文献[4-5]中存在的问题没有给出合理的解释，得出结论有点偏颇;文献[8]证明了整体最小二乘线性回归条件平差法与间接平差法解的等价性问题，没有就精度估计等价性给出理论上的证明。考虑到上述这些因素，本文采用测量平差中处理数据建模的方法，对整体最小二乘线性回归参数的求解进行较为深入的研究，旨在为整体最小二乘理论在测量数据处理中的应用奠定研究基础。

二、自变量无误差的线性回归模型

为了讨论问题方便起见，以一元线性回归为例，设观测点坐标为(xi，yi)，则一元线性回归模型为

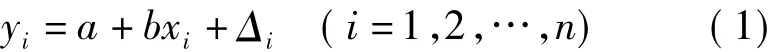
式中，a、b为回归参数;Δi为观测量yi的真误差。

如果自变量xi没有误差，设未知参数a、b的近似值为a0、b0，其改正数为 d a，d b。按间接平差求解，其误差方程式为

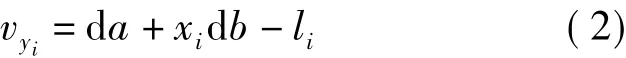
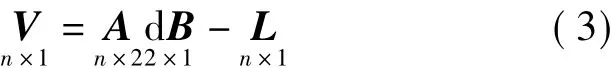
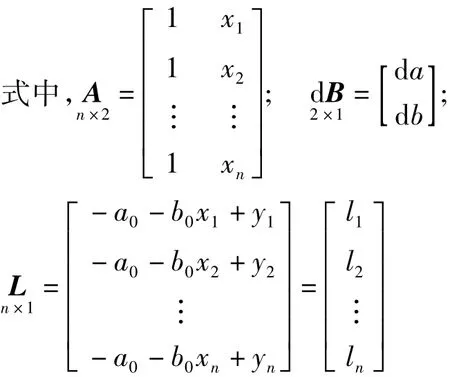
假设 Pyy为观测量 y的权阵，在最小二乘准则VTPyyV=min下，则回归参数改正数的估值为

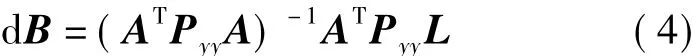
三、顾及自变量误差的线性回归模型

1．顾及自变量误差的条件平差模型

如果考虑自变量x误差，并假设x与y相互独立，则其回归模型观测方程为

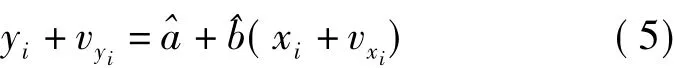
式中，vxi、vyi为观测量的改正数。式(5)是含参数与观测量改正数的二次项，将未知参数a、b的近似值a0、b0代入式(5)，线性化后约去参数与观测量改正数的二次项，则观测方程可表示为

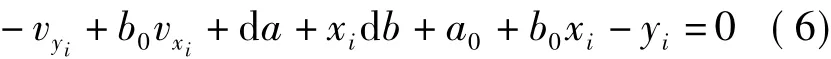
其矩阵表达式为

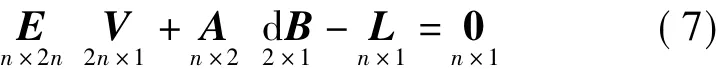
式(7)表示包含残差及未知参数改正数组成的约束方程，每一个观测数据点组成一个方程，共n个方程，式中待定量共2n+2个(其中，包括两个参数，2n个Vx与Vy)，故需最小二乘准则进行解算。

考虑到自变量x与因变量y的独立性且不等精度，其随机模型为

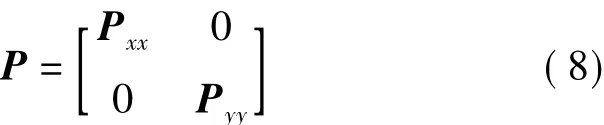
由最小二乘估计准则VTPV=min，构造极值函数φ=VTPV-2KT(EV+A d B-L)，K为联系数向量矩阵。由极值函数对V、d B分别求偏导数，可得

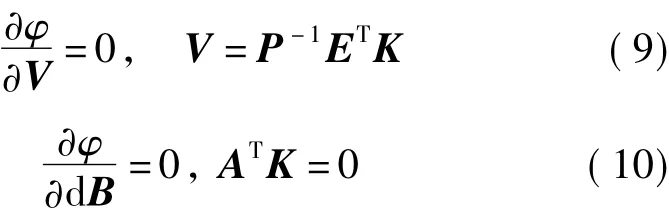
联立式(7)、式(9)、式(10)可得到 K、V、d B 的唯一解

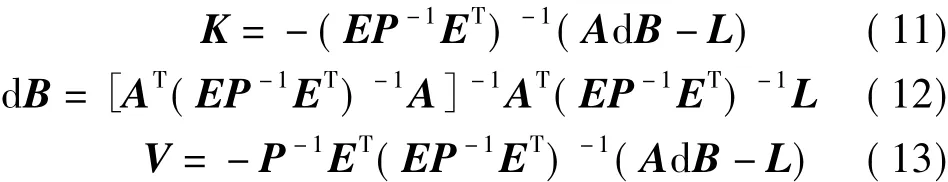
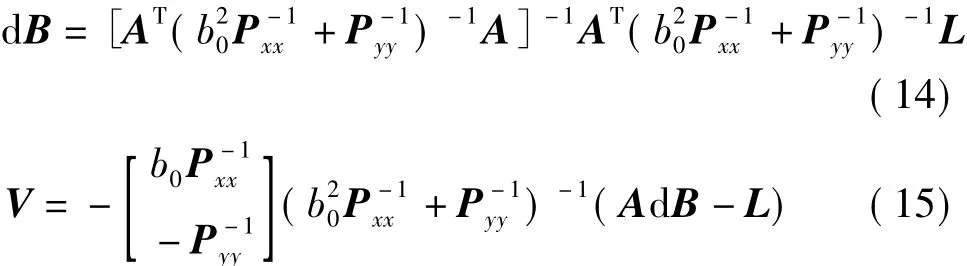
则回归参数的估值为

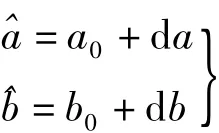
2．顾及自变量误差的间接平差

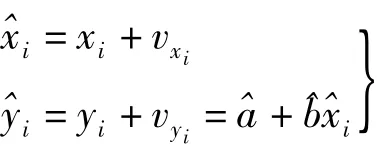
取xi0=xi，将未知数的近似值代入上述平差方程，将观测方程线性化，约去参数改正数的二次项，则误差方程为

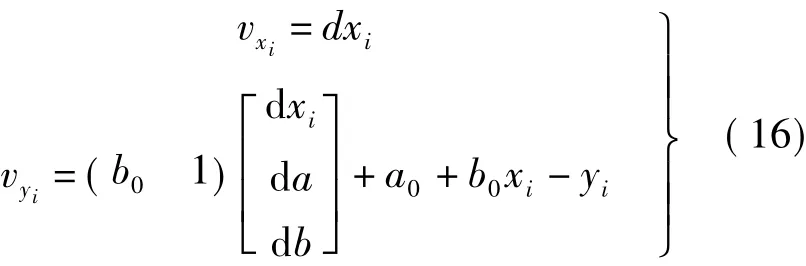
其矩阵表达式为

式中

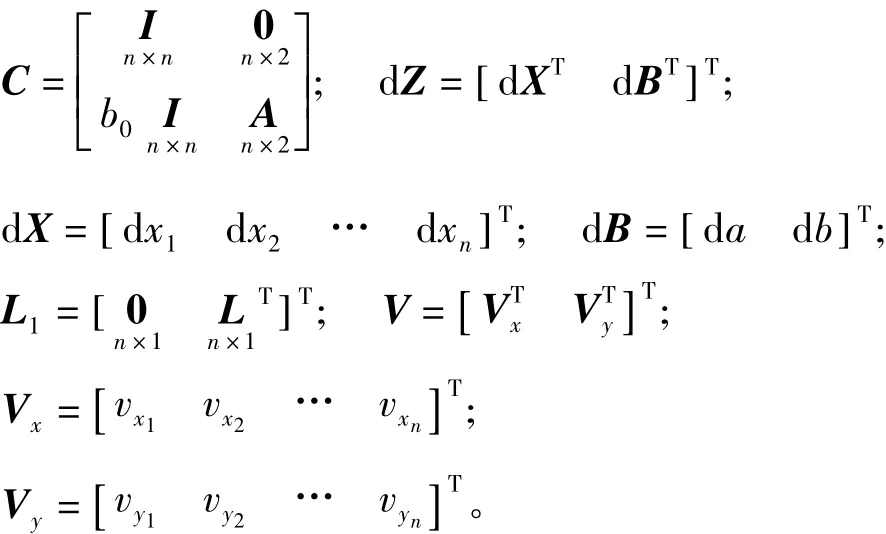
按间接平差原理，组成法方程可得

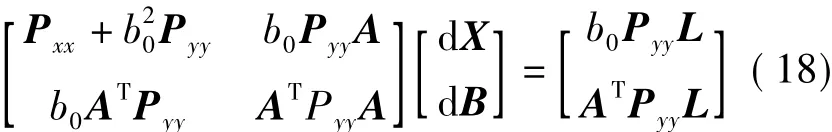
由式(18)第一个方程可得

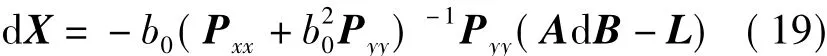
将式(19)代入式(18)第二式可得

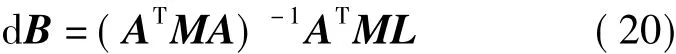
3．顾及自变量误差的两种平差方法的等价性

为了证明上述两种平差方法的等价性，比较式(20)与式(14)，只需证明式(21)成立

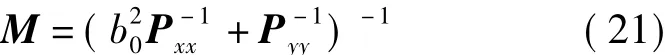
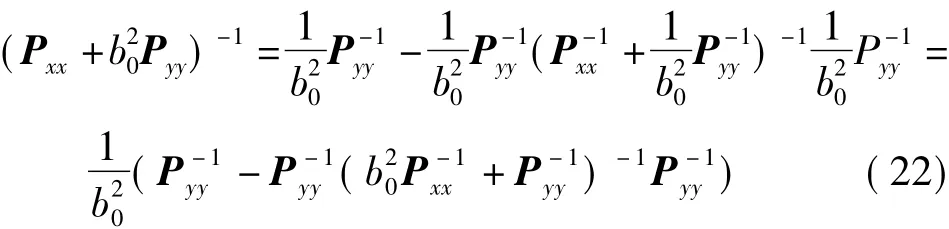
将式(22)代入下式整理得

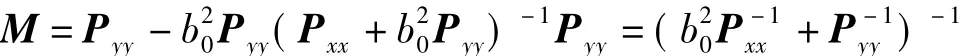
即式(21)得证，由此可见参数的解式(14)与式(20)等价。

同样可以证明两种平差方法所得到的观测量改正数相等的结论，将式(19)代入式(17)得到

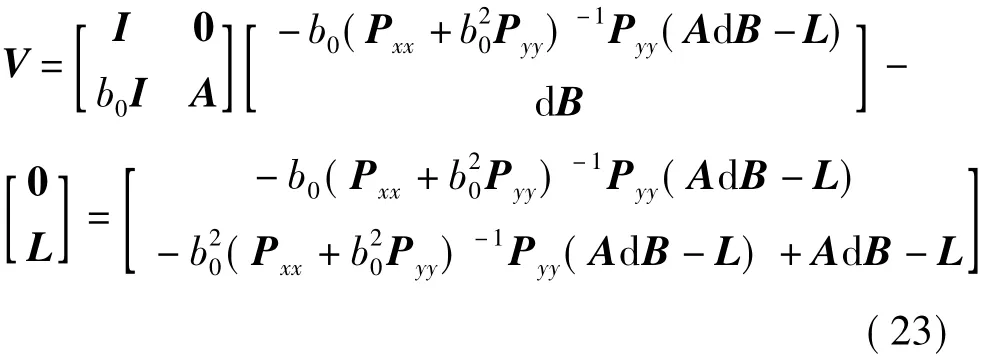
对式(23)进一步整理得

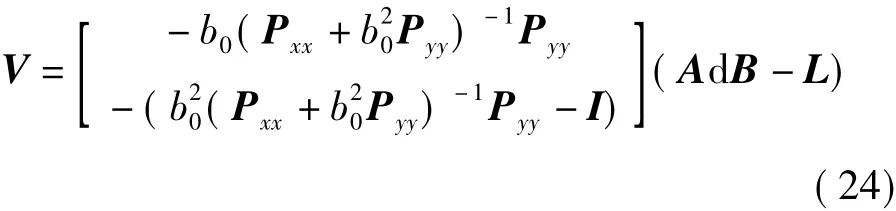
由矩阵的恒等性质可知，如果矩阵A与B是正则方阵，则矩阵恒等式成立，利用该矩阵恒等性质，则式(24)中矩阵的第一式改化为

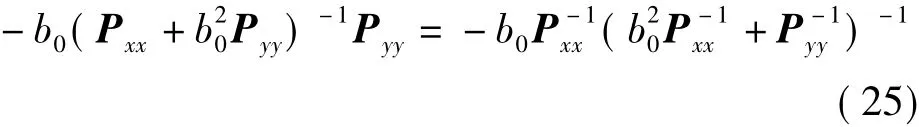
由矩阵的反演公式，将式(25)中矩阵的第二式改为

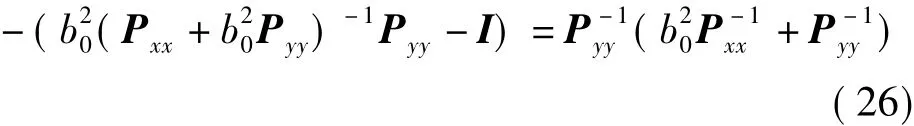
将式(25)和式(26)代入式(24)整理得

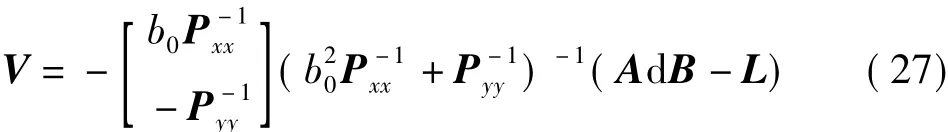
比较式(27)与式(14)，即结论成立。

4．顾及自变量误差线性回归解的精度估计

观测量的标准差按下式估计

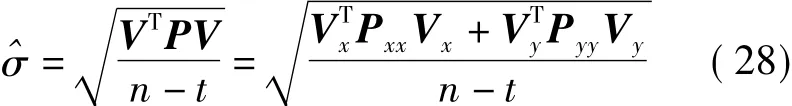
式中，n为观量数据点数;t为回归参数的个数，对于一元线性回归而言t=2。

就参数的方差与协方差的计算，按方差传播定律，由式(20)可得到参数的方差为

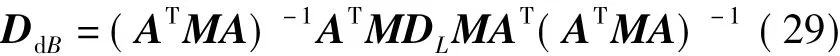
式中，DL为L的方差。由于其向量形式为

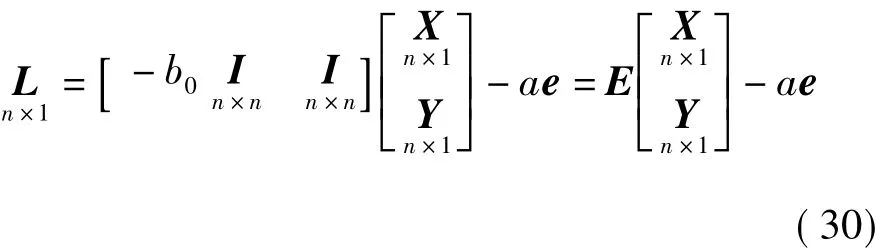
式中e=[1 1 …1]T。由式(30)可得L的方差阵为

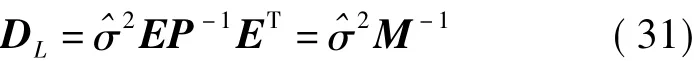
将式(31)代入式(29)得

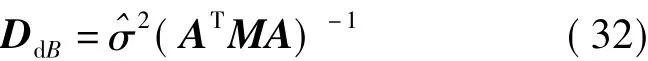
四、结束语

回归分析方法是一种处理测量数据常用的方法，本文在同时考虑观测数据xi与yi的误差的前提下，应用整体最小二乘原理，导出了整体最小二乘线性回归模型的解。按照间接平差与条件平差的原理，证明了整体最小二乘线性回归模型参数的解以及标准差的等价性。

[1]GOLUBG H，VAN L C F．An Anlysis of the Total Least Squares Problem[J]．SIAM J．Nuner．Anal，1980，17：883-893．

[2]愈锦成．关于整体最小二乘问题的可解性[J]．南京师大学报：自然科学版，1996(1)：12-16．

[3]武汉大学测绘学院测量平差学科组．误差理论与测量平差基础[M]．武汉：武汉大学出版社，2003．

[4]刘大杰，史文中，童小华，等．GIS空间数据处理的精度分析与控制[M]．上海：上海科学技术文献出版社，1999．

[5]王安怡，陶本藻．顾及自变量误差的回归分析理论和方法[J]．勘察科学技术，2005(3)：29-32．

[6]李雄军．对 X和 Y方向最小二乘线性回归的讨论[J]．计量技术，2005(1)：50-52．

[7]鲁铁定，陶本藻，周世键．基于整体最小二乘法的线性回归建模和解法[J]．武汉大学学报：信息科学版，2008(5)：504-507．

[8]周世键，鲁铁定．双变量线性回归解算方法的等价性[J]．江西科学，2009(6)：867-870．

[9]孔建，姚宜斌，许双安．整体最小二乘求取坐标转换参数[J]．大地测量与地球动力学，2010(3)：74-78．