正十二烷高温燃烧详细化学动力学机理的系统简化

方亚梅 王全德 王 繁,* 李象远

(1四川大学化学学院,成都610064; 2四川大学化学工程学院,成都610065)

正十二烷高温燃烧详细化学动力学机理的系统简化

方亚梅1王全德1王 繁1,*李象远2,*

(1四川大学化学学院,成都610064;2四川大学化学工程学院,成都610065)

采用详细化学反应动力学机理的系统简化方法,以典型航空燃料的替代组分正十二烷为研究对象,开展了正十二烷高温燃烧化学动力学机理的系统简化.首先采用多步直接关系图法(DRG)和基于计算奇异值摄动法(CSP)重要性指标的反应移除方法对由1279个组分,5056个基元反应组成的正十二烷燃烧详细机理进行框架简化,得到了包含59个组分,222个基元反应的框架机理;进一步采用CSP对框架机理进行时间尺度分析,选出了10个准稳态物种,采用准稳态近似方法(QSSA)构建了包含49个组分的全局简化机理.计算结果表明,在较宽的参数范围内,框架机理和全局简化机理均能够重现正十二烷详细机理在高温燃烧的点火延迟时间、熄火以及物种浓度分布等方面的模拟结果.

正十二烷;详细反应动力学机理;机理简化;直接关系图;计算奇异值摄动法;准稳态近似

1 引言

到目前为止,人类社会使用的最普遍也是最重要的燃料是碳氢燃料,研究碳氢燃料燃烧反应动力学机理对于发动机燃烧室的设计、污染物的形成与控制等具有重要意义.1然而,实际应用的燃料组成复杂,通常包括几十乃至上百种复杂的碳氢化合物.为了构建实际燃料燃烧的化学动力学模型,采用分别构建实际燃料涉及到的每一种组分的燃烧机理,然后再耦合起来的方法在实际应用中是不可行的.因此,构建实际燃料燃烧反应动力学机理时,一般按照化学组成、碳氢比以及积碳指数等目标选取三到五种碳氢化合物作为替代燃料,然后构建替代燃料的详细反应机理.2由于要求详细机理能在较大范围内变化的温度、压力、当量比等条件下都适用,导致碳氢燃料燃烧的详细化学反应动力学机理一般非常复杂,尤其是详细机理的物种数目随燃料分子尺寸的增加呈指数增长.1因此除了分子尺寸很小的燃料如甲烷等,其动力学机理相对简单,对于分子尺寸较大的反应物,其燃烧的详细动力学模型会非常复杂.1

在发动机数值模拟中,为了更准确地模拟燃烧室内的燃烧和流场情况,深入研究燃料燃烧情况对发动机性能以及污染物形成的影响,在进行计算流体力学(CFD)模拟时必须把燃料燃烧的动力学机理与流动方程组耦合起来进行数值求解.目前CFD模拟燃烧过程常常采用只包含一步或者少数几步总包反应的极度简化的燃烧动力学模型,这种燃烧动力学模型的适用范围通常比较小,模拟结果的可靠性也不高.然而,如果在CFD模拟中直接使用详细的燃烧动力学机理除了会使计算量大得难以承受外,在计算理论上也会带来巨大难题:1一是详细机理中物种数目过于庞大,以目前的计算条件,在三维CFD模拟中难以容纳这么多的物种;二是各种化学组分及其涉及的反应特征时间尺度差异巨大,导致研究和计算的对象变为极强的刚性系统,该系统的可靠和精密求解是较为困难的.因此,要得到可靠的模拟结果,就必须在保证机理模拟精度的条件下对详细动力学机理进行简化.另一方面,对详细机理的简化有利于更加深入地对燃料燃烧化学过程进行系统分析,研究对燃烧过程起关键作用的化学反应和物种,从而有助于燃料设计和对污染物的控制等.

由于机理简化的重要性,目前机理简化的方法也得到了迅速的发展.机理简化方法可以分成两类,3第一类是框架简化,即从详细机理中去掉不重要的物种和基元反应而得到框架机理;第二类方法是时间尺度分析方法,通过分析各反应的时间尺度降低计算的刚性.基于第一类的方法主要有计算奇异摄动法(CSP)、3,4灵敏度分析法、5主成分分析方法(PCA)6等.2005年,Lu和Law7提出了直接关系图法(DRG),该方法可以清楚反映指定物种的反应路径,同时机理简化的计算量与物种数目呈线性关系,是近年来出现的最新和前沿的简化方法之一,得到了迅速的推广和改进.8-10基于第二类的方法主要有准稳态近似法(QSSA)、11计算奇异摄动法、12本征低维流形法(ILDM)13等.事实上,CSP与ILDM方法的基本思路和QSSA方法类似,区别主要在于QSSA方法中先判断处于准稳态的物种,并假设在整个时间和空间区域里这些物种的净生成速率都为零,而CSP方法和ILDM方法需要在各个计算时间点和空间点判断处于准稳态的物种.因此,通过合理地选择准稳态组分,结合QSSA方法,构建能在很宽的范围内重现详细机理模拟结果的全局简化机理是最常用的时间尺度简化方法.1针对物种数和反应数较多的详细机理,在具体的简化工作中,通常按照一定简化顺序综合以上的各种方法来得到一个最优的简化机理.1

正十二烷是航空煤油的重要成分,也是构建航空煤油替代模型的常用组分,因此正十二烷燃烧化学动力学详细机理的构建和系统的简化对于航空发动机数值模拟具有重要意义,相关工作得到了广泛的研究,You、14华晓筱15和Herbinet16等分别构建了正十二烷燃烧详细化学动力学机理并进行了模拟,You14和华晓筱15等还分别对其构建的详细机理进行了系统地简化.最近,Westbrook等17依据反应类规则构建了正十二烷燃烧详细机理,其中包含有1279个组分与5056个反应,该机理能够较好地重现正十二烷低温以及高温燃烧的性质.本文对Westbrook等构建的正十二烷高温燃烧详细化学动力学机理进行了系统简化,首先通过多步DRG法和基于CSP重要性指标的反应移除方法对详细机理进行框架简化,得到包含59个组分、222步基元反应的框架机理;在此框架机理的基础上,采用CSP方法识别准稳态物种,结合QSSA方法,构筑了只包含49个物种的全局简化机理;模拟结果表明简化的反应机理能够在很宽的模拟条件内重现正十二烷高温燃烧详细机理的点火、熄火以及物种浓度分布等模拟结果.

2 简化计算方法

2.1 框架简化方法

由于详细机理中组分之间的复杂耦合关系导致查明和去除非重要组分较为困难.2005年,Lu和Law7提出了直接关系图法,为检查组分间的耦合关系和去除不重要的物种提供了一个很好的办法.由于其简化效率非常高,通常用于含较多组分机理的简化过程的第一步.该方法的基本思路为:如果某组分B的去除将导致组分A的生成或消耗产生较大误差,则对于A组分来说,B组分是重要的.为了定量描述组分B对组分A的影响,Law等定义如下关系:

其中rAB为组分B对组分A的正归化贡献,ωi为第i个基元反应的净反应速率,νA,i为A在第i个基元反应的化学计量系数,I为基元反应总个数.可以看到,rAB足够大时,去除组分B将导致A的生成或者消耗产生较大误差,此时,组分A显著依赖于组分B.具体编程实现DRG方法时,初始设定一个阈值ε,选定初始重要组分,采用深度优先搜索方法进行搜索得到重要组分,然后删除不重要的物种及其涉及的反应,得到简化的框架机理.一般地,对于组分数比较多的详细机理,随着组分的移除,保留组分的rAB会随之变化,所以通常采用多步DRG方法得到尽可能简化的机理,并且得到的框架机理的精度会提高.

采用DRG方法删除不重要物种之后,一般采用敏感度分析、主成分分析或计算奇异摄动法等方法继续删除不重要反应.采用敏感度分析方法尽管能有效删除多余反应,但是敏感度分析方法计算量较大,因此这里我们采用Lu和Law18提出的基于CSP重要性指标的反应移除方法来进一步简化框架机理.此方法不将可逆反应的正逆反应分开,而是作为一个反应进行计算,因此可以准确判断能快速达到偏平衡的可逆反应的重要性.将判断反应重要性的指标定义如下:

通过此方法进行简化时,首先设定重要组分和阈值,计算重要组分的IA,i,并保留IA,i大于所设定阈值的反应.

2.2 基于CSP的准稳态方法

准稳态方法通过把化学反应时间尺度小的物质设定为准稳态物种,不求解相应物种浓度的微分方程,而是通过假设该物种浓度随时间的变化率为零计算准稳态物种的浓度,从而降低了计算的刚性.应用准稳态方法需要解决两个主要的问题:1首先是准稳态物种的选择,这直接影响简化机理的模拟精度,其次是对准稳态物种浓度的可靠和有效求解.对于准稳态物种的选取方法有两种,第一种是通过准稳态物种的定义来选取,即将生成速率近似等于消耗速率并且浓度较小的组分做为准稳态物种.Chen11开发的简化动力学模型的CARM软件以及钱炜祺等开发的SPARCK软件21就是通过此方法来选择准稳态物种,此方法简单、使用方便,但是不够精确,并且由于组分浓度的变化率是通过基元反应速率的组合来计算,组分浓度的变化率对组分的导数也不易求取,不便于耦合到流场计算中使用;20第二种是利用CSP方法进行时间尺度分析,将反应系统分为快模式或慢模式,再通过考察物种对快反应或者慢反应模式的贡献,从而选取准稳态物种.此方法是通过对Jacobian矩阵进行分析,使组分的反应空间解耦合为快慢两个模式.这个方法能够更加合理的选择准稳态物种,但是由于需要计算Jacobian矩阵,计算量比传统模型有所增加.基于CSP方法选择准稳态物种的方法如下:

一般地,对一个包含有N种组分和I个基元反应的化学反应动力学模型有:

其中,ca为第a个物种的浓度.上式中化学反应速率fa对时间的变化率可以表达为

其中J是Jacobian矩阵.CSP方法通过对J做相似变换:Λ=X·J·Y,其中,X和Y是基向量,并且X=Y-1,Λ为对角化或者块对角化矩阵,再通过如下两步修正得到基向量以及将快慢模式解耦合:4

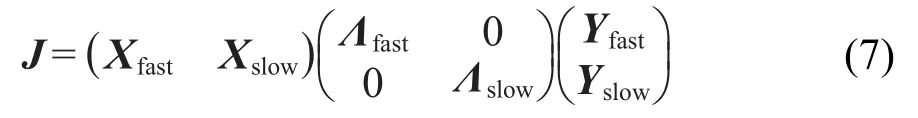
基于上述理论,Lu等提出了一种准稳态物种的识别方法:21

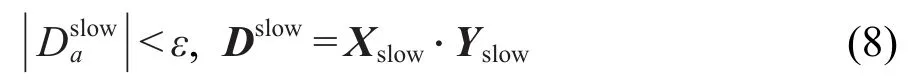
其中ε是阈值,即把对慢模式贡献较小的组分设定为准稳态组分.此方法的优点在于不会将部分平衡的物种选作准稳态物种,因此结果更加精确.对于求解准稳态物种的浓度,本文中采用定点迭代求解22的方法,这也是目前应用较广泛的方法.此方法的缺点为:如果两个或多个准稳态物种耦合强烈的情况下可能会收敛很慢甚至会出现不收敛的情况,影响计算效率和结果.

3 正十二烷高温燃烧简化动力学机理的构建

3.1 框架简化结果

本文用CHEMKIN2.0-SENKIN程序23,24对正十二烷高温恒压点火的模拟结果作为分析基础,DRG方法所用数据点来自当量比(φ)分别为0.5、1.0和1.5,初始温度为1000、1100、1200、1400和1600 K,压力(p)在1.0×105和1.0×106Pa条件下恒压自动点火模拟中点火延迟时间附近的SENKIN程序结果抽样.

我们首先采用DRG方法作为框架简化的第一步,以去除冗余的组分及相应的反应.在这一步简化中,我们将反应物和产物nC12H26、CO2、H2O、N2、O2设为重要组分,通过设定不同阈值ε得到单步DRG简化机理.DRG方法简化机理时,只需要将必要的组分选为重要组分即可,不同的选取方法对简化结果影响不大.图1为不同阈值条件下得到的框架机理的组分数以及框架机理与详细机理相比计算点火延迟时间的平均误差.可以看出随着阈值的增加,得到框架机理组分数越少,同时框架机理的误差也逐渐增加,当阈值在0.23附近时,平均误差随着阈值的增加迅速增加.在实际应用中一般通过把误差控制在某特定范围内(通常控制误差在30%以内)来选取适当的阈值,因此本文选取阈值为0.22,得到的框架机理包含63个组分,295个反应.

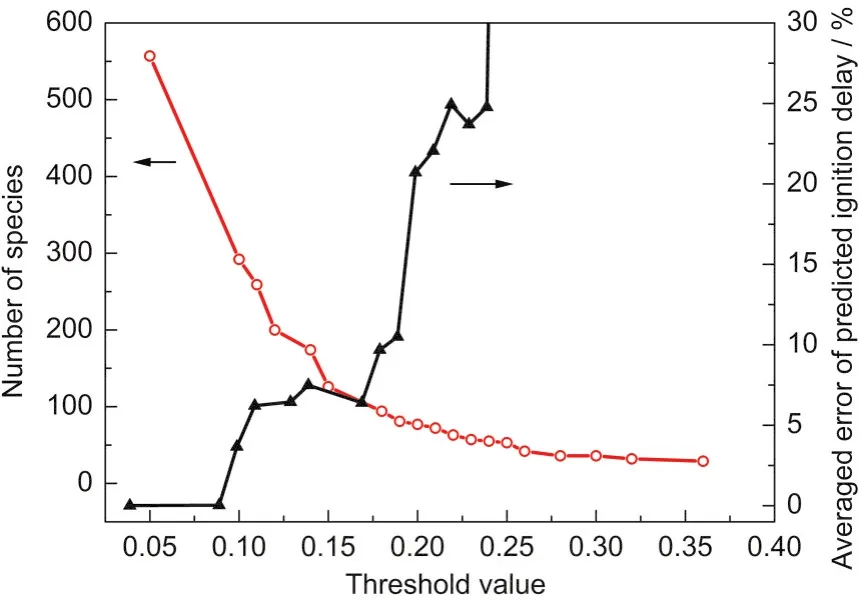
图1 采用DRG方法时取不同阈值得到框架机理的物种数和点火延迟时间的平均误差Fig.1 Number of species of skeletal mechanism generated by DRG as a function of threshold values and the averaged error of predicted auto-ignition delay time of the skeletal mechanisms

为了得到更加简化的框架机理,Lu等25提出了多步DRG方法,即在DRG方法的基础上再完成一步或者两步DRG简化.一般地,对于比较庞大的详细机理,通过两步或者三步DRG方法可以得到基于DRG方法的最小简化框架机理.两步DRG与单步DRG方法所取阈值不同.通常,两步DRG方法中第一步DRG所设定阈值比单步DRG的阈值稍小,而第二步DRG比单步DRG阈值大.通过设定不同阈值,两步DRG相比于单步DRG会有较好的简化结果,即得到的框架机理包含较少的组分,同时与详细机理的计算结果比较有较小的误差.本文中,我们也采用了两步DRG方法简化正十二烷燃烧的详细机理,其中第一步和第二步DRG方法设定的阈值分别为0.18和0.20,得到的框架机理包含59个组分和270个反应.这样得到的框架机理不能再继续通过DRG方法删除物种,否则误差会急剧增加.图2是详细机理、单步DRG与两步DRG方法得到的点火延迟结果.从图2可以看出,通过两步DRG得到的框架机理有更少的组分和反应,但是点火延迟与详细机理符合得更好.为了进一步简化框架机理,我们采用基于CSP重要性指标的方法去除多余物种,设定框架机理中所有组分为重要组分并选取反应的阈值为0.01,在59组分框架机理的基础上删除了48个反应,最终得到包含59组分和222个基元反应的框架机理.

3.2 全局简化机理的构建

对3.1节中得到的框架机理,我们采用CSP方法对SENKIN程序在温度为1000、1200、1400和1600 K,压力为1.0×105和1.0×106Pa,当量比为0.5、1.0和1.5时的恒压自动点火模拟结果进行抽样分析,设定Jacobian矩阵本征值小于-1.0×105的模式为快模式,选取了|Dslowa|小于1.0×10-4的10个物种(C2H3O1-2,C4H7,C8H17-4,C10H21-1,C6H13-1,C12H25-5, C12H25-3,C5H11-1,C7H15-1,C8H17-2,短横线后面的数字代表物种中自由基的位置)作为准稳态物种,结合QSSA,构建了包含49个组分,45步反应的全局简化机理.

图2 详细机理与通过单步DRG与两步DRG方法得到的包含63和59个组分的框架机理模拟的正十二烷高温燃烧的点火延迟时间Fig.2 Ignition delay time of high-temperature oxidation of n-dodecane with detailed mechanism and 63-species and 59-species mechanism generated by one-step and two-step DRGτign:ignition delay time,φ:equivalence ratio

4 框架机理与简化机理的验证

图3 在不同初始温度、当量比、压力条件下,正十二烷高温燃烧的59组分框架机理、49组分简化机理与详细机理点火延迟时间的比较Fig.3 Ignition delay time of n-dodecane,as a function of initial temperature for different pressures and equivalence ratios, with detailed mechanism,59-species skeletal mechanism,and 49-species reduced mechanism

图4 含59个组分的框架机理、含49个组分的简化机理与详细机理在大气压下、初始温度为1400 K时不同当量比条件下温度随时间的变化以及当量比为1.0、初始温度为1200 K时物种浓度随时间变化比较Fig.4 Temperature profiles in auto-ignition simulation with constant pressure,different equivalence ratios and initial temperature of 1400 K,and species profiles with constant pressure,equivalence ratio of 1.0 and initial temperature of 1200 K calculated with detailed mechanism,59-species skeletal mechanim,and 49-species reduced mechanismblack lines:detailed mechanism,colorful lines:skeletal mechanism,symbols:reduced mechanism

为了验证得到的框架机理和简化机理的有效性,采用CHEMKIN2.0中的SENKIN模块分别用详细机理、框架机理和全局简化机理计算了正十二烷在不同条件下的点火延迟时间并进行了比较.图3给出了在不同初始温度、压力(p)和当量比(φ)条件下的恒压点火延迟比较.可以看出,在1.0×105和5.0× 105Pa时框架机理和全局简化机理都较好地重现了详细机理的模拟结果.但是在压力为3.0×106Pa、初始温度为1000 K左右时,点火延迟有较大误差.这主要是由于简化时抽样的反应状态点是高温的反应条件,因此得到的框架机理和简化机理仅适用于高温,而当压力比较高或起始温度较低时,低温燃烧机理对点火延迟时间的影响逐渐增加,因此框架机理和简化机理此时计算误差比较大.这也表明通过上述简化过程得到的框架机理和简化机理都只适用于初始温度高于1000 K,压力为1.0×105到3.0× 106Pa的高温和压力模拟范围.图4分别给出了初始温度为1400 K,压力为1.0×105Pa和不同当量比条件下恒压点火模拟时温度随时间的变化以及在初始温度1200 K,1.0×105Pa,当量比为1.0时恒压自动点火模拟过程中主要组分O2、CO、C2H4和nC12H26浓度随时间的变化.由图4可以看出,框架机理、全局简化机理与详细机理的模拟结果吻合比较好,而全局简化机理与框架机理的模拟结果差别很小,可见由准稳态方法简化所产生的误差很小,全局简化机理与详细机理的模拟结果差别主要来自于框架简化机理的误差.

熄火是在航空发动机燃烧室设计中需要考虑的重要性质.为了进一步验证简化机理在熄火条件下的应用,我们采用全混流反应器(PSR)26模拟了1.0×105Pa条件下,不同当量比下滞留时间和温度的关系曲线,在所有模拟中进气温度为300 K.从图5可以看出,框架机理和全局简化机理能较精确地重现详细机理的温度曲线,尤其是在拐点处的滞留时间(熄火).

图5 PSR模拟正十二烷59组分框架机理和49组分简化机理与详细机理在300 K,1.0×105Pa下,不同当量比和滞留时间条件下温度曲线的比较Fig.5 Temperature profiles of PSR at different residence time with constant pressure of 1.0×105Pa and various equivalence ratios at fixed inlet temperature of 300 K, calculated with detailed mechanism,59-species skeletal mechanism,and 49-species reduced mechanismblack lines:detailed mechanism,colorful lines:skeletal mechanism symbols:reduced mechanism

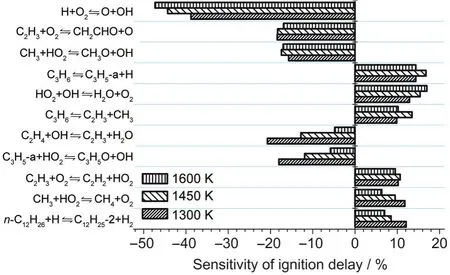
图6 正十二烷高温燃烧框架机理的敏感度分析Fig.6 Sensitivity analysis for the skeletal mechanism for high-temperature oxidation of n-dodecane

从上述模拟结果可以看出,与详细机理相比,我们通过系统的简化过程得到的正十二烷高温燃烧的59组分框架机理和49组分全局简化机理在一个较宽的参数范围内能可靠地模拟正十二烷的点火和熄火过程.

5 敏感度分析

敏感度分析方法对判断化学反应动力学模型中的关键反应有重要作用.本文对点火延迟进行敏感度分析,从而判断对点火延迟时间起关键作用的反应.对敏感度系数(S)定义如下:10,15,27

其中,ki是基元反应i的反应速率常数,τign(ki)是反应速率常数加倍前的点火延迟时间,τign(2ki)是反应速率常数加倍后的点火延迟时间.若敏感度系数大于零,则该反应对点火延迟起抑制作用;反之,起促进作用.

图6给出了对正十二烷高温燃烧的59个组分, 222个基元反应的框架机理进行敏感度分析,敏感度系数最大的11个基元反应,其中模拟条件为在1.0×105Pa下,当量比为1.0时,起始温度为1300、1450与1600 K的恒压自动点火.从图中可以看出,反应H+O2⇌O+OH对点火延迟有最大的促进作用,并且小分子反应对点火的影响很大.

6 结论

基于详细化学动力学模型的系统简化方法,本文对Westbrook等最近构建的包含1279个物种和5056步基元反应的正十二烷燃烧详细化学反应机理进行了系统简化.采用两步DRG方法和基于CSP重要性指标的反应移除方法,构建了包含59个物种和222步基元反应的正十二烷高温燃烧化学动力学框架机理.通过对多步DRG与单步DRG简化结果的比较发现,对于组分数较多的详细机理的简化,两步DRG方法与单步DRG方法相比更适用.在此基础上,我们进一步采用CSP方法对框架机理进行时间尺度分析,依据物质在慢模式中的贡献进行准稳态物种的精确识别,在此基础上结合QSSA方法构筑了包含49个组分的全局简化机理.模拟结果表明,框架机理和全局简化机理都能在较宽的模拟条件下,重现详细机理对点火延迟时间、主要物种浓度变化和熄火等模拟结果.与详细机理相比,框架机理更容易用于分析正十二烷高温燃烧中所涉及的重要物种和反应.虽然我们得到的全局简化机理在用于CFD模拟时所含物种数仍然较多,但是随着计算机技术和CFD模拟软件的发展,将来可能能够用于CFD仿真模拟.此外,由于正十二烷低温燃烧机理更加复杂,我们还将结合集总等方法针对低温机理开展进一步的简化研究工作.

Supporting Information: The skeletal mechanism and reduced mechanism are generated in a wide domain,equivalence ratios range from 0.5 to 1.5,temperatures range from 1000 to 1600 K and pressures are 1.0×105and 3.0×106Pa.This information is available free of charge via the internet at http://www. whxb.pku.edu.cn.

Reference

(1) Lu,T.F.;Law,C.K.Prog.Energy Combust.Sci.2009,35,192. doi:10.1016/j.pecs.2008.10.002

(2) Dagaut,P.;Cathonnet,M.Prog.Energy Combust.Sci.2006,32, 48.doi:10.1016/j.pecs.2005.10.003

(3)Valorani,M.;Creta,F.;Goussis,D.A.;Lee,J.C.;Najm,H.N. Combust.Flame 2006,146,29.doi:10.1016/j.combustflame. 2006.03.011

(4) Lam,S.H.Combust.Sci.Technol.1993,89,375.doi:10.1080/ 00102209308924120

(5)Rabitz,H.;Kramer,M.A.;Dacol,D.Annu.Rev.Phys.Chem. 1983,34,419.doi:10.1146/annurev.pc.34.100183.002223

(6) Vajda,S.;Valko,P.;Turanyi,T.Int.J.Chem.Kinet.1985,17, 55.doi:10.1002/(ISSN)1097-4601

(7) Lu,T.F.;Law,C.K.Proc.Combust.Inst.2005,30,1333.doi: 10.1016/j.proci.2004.08.145

(8) Pepiot-Desjardins,P.;Pitsch,H.Combust.Flame 2008,154,67. doi:10.1016/j.combustflame.2007.10.020

(9) Sun,W.;Chen,Z.;Gou,X.;Ju,Y.Combust.Flame 2010,157, 1298.doi:10.1016/j.combustflame.2010.03.006

(10)Wang,Q.D.;Fang,Y.M.;Wang,F.;Li,X.Y.Combust.Flame 2012,159,91.doi:10.1016/j.combustflame.2011.05.019

(11) Chen,J.Y.Combust.Sci.Tech.1988,57,89.doi:10.1080/ 00102208808923945

(12) Lam,S.H.;Gousiss,D.A.Int.J.Chem.Kinet.1994,26,461. doi:10.1002/(ISSN)1097-4601

(13) Maas,U.;Pope,S.B.Combust.Flame 1992,88,239.doi: 10.1016/0010-2180(92)90034-M

(14)You,X.;Egolfopoulos,F.N.;Wang,H.Proc.Combust.Inst. 2009,32,403.doi:10.1016/j.proci.2008.06.041

(15)Hua,X.X.;Wang,J.B.;Wang,Q.D.;Tan,N.X.;Li,X.Y.Acta Phys.-Chim Sin.2011,27,2755.[华晓筱,王静波,王全德,谈宁馨,李象远.物理化学学报,2011,27,2755.]doi:10.3866/ PKU.WHXB20112755

(16) Herbinet,O.;Marquaire,P.M.;Battin-Leclerc,F.;Fournet,R. J.Anal.Appl.Pyrolysis 2007,78,419.doi:10.1016/j.jaap. 2006.10.010

(17) Westbrook,C.K.;Pitz,W.J.;Herbinet,O.;Curran,H.J.;Silke, E.J.Combust.Flame 2009,156,181.doi:10.1016/ j.combustflame.2008.07.014

(18) Lu,T.F.;Law,C.K.Combust.Flame 2008,154,153.doi: 10.1016/j.combustflame.2007.11.013

(19) Zhan,H.;Qian,Z.Q.Computers and Applied Chemistry 2007, 24,1484.[詹 浩,钱祉祺.计算机与应用化学,2007,24, 1484.]

(20) Qian,W.Q.;Yang,S.H.;Xiao,B.G.;Le,J.L.Chinese Journal of Theoretical and Applied Mechanics 2007,39,37. [钱炜祺,杨顺华,肖保国,乐嘉陵.力学学报,2007,39,37.]

(21) Lu,T.F.;Law,C.K.Combust.Flame 2008,154,761.doi: 10.1016/j.combustflame.2008.04.025

(22) Chen,J.Y.;Tham,Y.F.Combust.Flame 2008,153,634.doi: 10.1016/j.combustflame.2007.12.006

(23) Kee,R.J.;Rupley,F.M.;Miller,J.A.Chemkin-II:A Fortran Chemical Kinetics Package for the Analysis of Gas-Phase Chemical Kinetics.Report,SAND89-8009.Sandia,1989.

(24) Lutz,A.E.;Kee,R.J.;Miller,J.A.Senkin:a Fortran Program for Predicting Homogeneous Gas Phase Chemical Kinetics with Sensitivity Analysis.Report,SAND87-8248.Sandia,1990.

(25) Lu,T.F.;Law,C.K.Combust.Flame 2006,144,24.doi: 10.1016/j.combustflame.2005.02.015

(26) Glarborg,P.;Kee,R.J.;Grcar,J.F.;Miller,J.A.PSR:A FORTRAN Program for Modeling Well-Stirred Reactors.Report SAND86-8209.Sandia,1986.

(27)Kumar,K.;Mittal,G.;Sung,C.J.;Law,C.K.Combust.Flame 2008,153,343.doi:10.1016/j.combustflame.2007.11.012

June 13,2012;Revised:August 20,2012;Published on Web:August 20,2012.

Reduction of the Detailed Kinetic Mechanism for High-Temperature Combustion of n-Dodecane

FANG Ya-Mei1WANG Quan-De1WANG Fan1,*LI Xiang-Yuan2,*
(1College of Chemisry,Sichuan University,Chengdu 610064,P.R.China;2College of Chemical Engineering, Sichuan University,Chengdu 610065,P.R.China)

The detailed chemical kinetic mechanism for high-temperature combustion of n-dodecane was systematically reduced via integrated mechanism reduction methods.The skeletal mechanism,including 59 species and 222 elementary reactions,was derived using the directed relation graph method(DRG) combined with a method based on computational singular perturbation(CSP)importance index from a detailed mechanism consisting of 1279 species and 5056 elementary reactions.The skeletal mechanism was further reduced through time-scale analysis.The CSP method was employed for the selection of quasi steady state(QSS)species,and ten species were chosen as QSS species.Finally,based on the quasi steady state approximation method,a 49-species reduced mechanism was derived.Both the skeletal mechanism and the 49-species reduced mechanism reproduced the ignition delay time,extinction,and species profiles of the detailed mechanism over a wide range of simulation conditions.

n-Dodecane;Detailed chemical kinetic mechanism;Mechanism reduction;Directed relation graph;Computational singular perturbation;Quasi-steady state approximation

10.3866/PKU.WHXB201208201

∗Corresponding authors.WANG Fan,Email:wangf@scu.edu.cn;Tel:+86-28-85406139.LI Xiang-Yuan,Email:lixy@scu.edu.cn; Tel:+86-28-85406139.

The project was supported by the National Natural Science Foundation of China(91016002,91116001/A0204).

国家自然科学基金(91016002,91116001/A0204)资助项目

O643