整周模糊度搜索空间确定方法研究*

陈 良 ，张泽建，吴 杰

(1国防科技大学航天与材料工程学院，长沙 4 10073;2 71834部队，河南荥阳 4 50100)

0 引言

随着GNSS技术的迅速发展，GNSS具有了为飞行器提供高精度导航信息的能力。为满足航空领域的精度需求，必须采用载波相位测量技术。由于GPS信号结构的限制，在相位观测量中总包含着一个未知的初始相位整周数。动态精密定位中，整周模糊度一般在模糊度域进行搜索确定。这类方法首先要确定初始解，即利用伪距和载波相位观测信息经联合平差得到模糊度初值，又称浮点解。一般采用在某一空间进行搜索的方法得到模糊度整周解。如何合理确定模糊度搜索空间是模糊度搜索方法的难点，也是不同模糊度搜索方法的主要区别之一。

1 几种动态模糊度初始化方法比较

目前利用较多的模糊度搜索方法有:AFM[1]、FARA[2－3]、FASF[3－5]、LAMBDA[6－13]和 Cholesky[14]分解方法等。其中，AFM在坐标域内进行搜索，其余几种方法均在模糊度域内进行搜索。目前各种单历元整周模糊度搜索方法普遍存在的问题是正确率难以保证，且计算效率低。FARA、FASF、LAMBDA和Cholesky分解快速模糊度搜索算法较适合动态模糊度求解，这几种方法均不同程度的利用了浮点模糊度的概率特性。FARA利用整个观测数据的残差及浮点模糊度每个元素的验后方差，获得模糊度矢量每个元素的初步搜索范围，搜索空间体积将非常大。为减小搜索空间，一般采用将浮点模糊度元素两两相减，利用模糊度元素之间的相关性，筛选出一部分待搜索值，但其计算量仍比较大。FASF利用序贯平差方法，先将前面元素值固定，后面元素的搜索区间受前面元素的影响，其搜索范围也会变小。FASF考虑的是前面选定的模糊度参数对后面的模糊度参数的综合影响，因此该方法得到的整周模糊度有效搜索空间要比FARA 小[15]。

LAMBDA和Cholesky方法对协方差矩阵的信息利用都比较充分，确定的整周模糊度空间比前两种方法都要小。LAMBDA是目前被广泛应用的方法，其理论体系也较为完整。Cholesky分解算法利用Cholesky一次分解得到空间变换矩阵。在变换后的空间内确定搜索范围，利用回归算法在原模糊度空间进行搜索，充分考虑了浮点模糊度的概率特性。

2 浮点模糊度的概率特性分析

若浮点模糊度精度足够高，各元素互不相关，则可对每个浮点模糊度元素取整直接得到整周模糊度。但因码伪距测量信息的参与，直接取整法确定的整周模糊度精度很低。Cholesky分解方法可实现浮点模糊度的完全去相关，但变换后的模糊度空间失去了原来的整数特性，最后的搜索还需要在原空间进行。模糊度矢量在两个空间之间的变换所需要的大量多维矩阵相乘运算增加了计算量。该方法完全从数学的角度进行变换，变换对精度追求过高，降低了搜索效率。若能在原浮点模糊度空间直接确定搜索空间，计算量将大大降低。

双差载波相位和伪距测量方程统一写为:

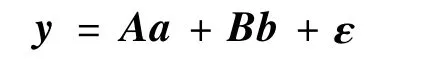
式中:y为双差观测量，a为模糊度矢量，b为基线矢量，ε为观测噪声。A和B为系数矩阵。利用加权最小二乘可得到浮点模糊度，基线矢量浮点解，以及浮点解协方差阵Q。

浮点模糊度虽然没有整数特性，但可最大程度满足方程，若不存在粗差，整周模糊度与浮点模糊度元素值相差不会很大。因此在观测条件良好情况下，模糊度每个元素的绝对搜索区间不应太大，大量的实验统计数据可支持这一观点。通过以下两组数据可看出，大部分模糊度真值与浮点模糊度比较接近。

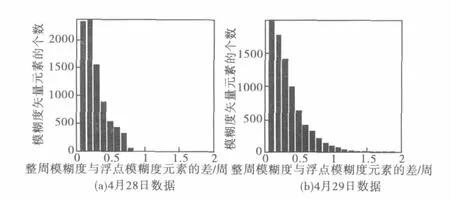
图1 整周模糊度和浮点模糊度比较

图1 为2010年4月28日和29日在试验楼顶试验台上的试验结果，历元数分别为1000和10000。在4月28日数据中，有1000个历元，期间可用卫星数为9～10，共有模糊度元素8250个。第一组数据浮点模糊度和整周模糊度的差值均小于0.8周，而且小于0.5周的元素有7455，说明该组数据测量精度较高。若在浮点模糊度左右 ±1的区间内进行搜索，整周模糊度真值将都包含在搜索空间内。若双差个数为8，则待搜索整周模糊度矢量个数为256。但不是所有测量数据都有这么高的测量精度。第二组数据有206个浮点模糊度与整周模糊度差值大于1周，差值均小于2。以上两组数据均在无明显多径反射环境下测得，但浮点模糊度精度有明显差别。因此要保证模糊度真值包含于搜索空间，模糊度元素的搜索区间应有余度。根据经验，若整周模糊度元素在以浮点模糊度对应元素为中心±3的区间内进行搜索，在没有粗差的条件下可保证模糊度真值在搜索范围内。实际上这个空间非常大，若双差个数为8，则搜索次数为5764801。如此大的搜索空间对于实时导航解算是无法接受的。

3 整周模糊度搜索空间的确定方法

从浮点模糊度的方差阵可直观地看出浮点模糊度各元素的求解精度及相关性。方差阵对角元素为浮点模糊度各元素的方差，方差阵其他元素为浮点模糊度各元素两两之间的协方差。利用这一信息对模糊度搜索空间进行压缩，具体实施过程如下:

1)按方差大小将浮点模糊度从新排序。查找在对角线上最小的元素q1，通过调整矩阵L1将它放在第1行第1列，得到矩阵:

同理，将次小元素q2放在第二行第二列。以此类推经n－1次变换得到矩阵:

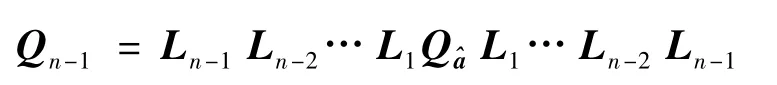
n为双差维数。因为方差阵对角元素反映了对应元素的精度，因此可得到每个元素的初始搜索区间为:

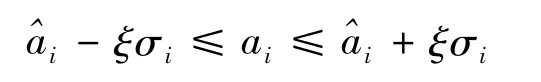
ξ为尺度因子，σi为双差模糊度元素的均方差。

2)利用协方差减小搜索区间。对矩阵Q前i行i列进行分块

利用下式确定模糊度每个元素的搜索区间。

其中:

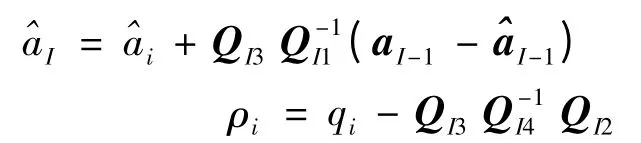
4 试验与分析

利用该方法对4月29日采集的数据重新在每一历元进行整周模糊度求解，与Cholesky分解快速模糊度搜索算法进行比对，整周模糊度的解完全一致。为验证方差阵分析法的有效性，另取一组观测环境较差的数据，进行整周模糊度的求解。该组数据共有10000历元。利用静态处理方法对10000个历元的观测数据进行处理，得到WGS84坐标系中基线矢量真值为[2.8375m，1.2019m，－4.3198m]，其精度和可信性较高。据此，分析不同整周模糊度求解方法的正确率，以及定位精度。不同方法的主要性能对比见表1，利用每个历元解算的整周模糊度进行的定位结果见图2。度求解正确率较高。但该方法中尺度因子的选择具有一定主观性，其最佳值与测量精度有关。在观测精度发生变化时尺度因子应具有自适应调整能力。还需在尺度因子如何恰当取值方面进行研究，以待完善。

表1 两种方法主要参数对比

图2 定位结果比较

与Cholesky分解快速模糊度搜索算法相比，方差阵分析法单历元平均搜索次数较少，整周模糊度求解正确率明显提高。从图2可明显看出方差阵分析法的定位结果更为稳定，说明该方法整周模糊度求解正确率较高。

5 结论

利用方差阵分析法进行整周模糊度搜索空间确定，可使待搜索的整周模糊度矢量数减少，搜索正确率提高，且不需要进行矩阵三角分解，提高了计算效率。特别是在观测质量较差的情况下，该方法的模糊

[1]Pretap Misra，Per Enge.全球定位系统—信号、测量与性能[M].罗鸣，曹冲，尚雄兵，等，译.2版.北京:电子工业出版社，2008.

[2]周忠谟，易杰军，周琪.GPS卫星测量原理与应用[M].2版.北京，测绘出版社，1997.

[3]E Frei，G Beutler.Rapid static positioning based on the fast ambiguity resolution approach"FARA":theory and first results[J].Manuscripta Geodaetica，1990，15(4):325－356.

[4]李淑慧，刘经南.基于搜索空间构造模糊度搜索方法的可靠性[J].测绘学院学报，2004，21(1):11－13.

[5]D Chen.Fast ambiguity search filter(FASF):A novel concept for GPS ambiguity resolution[C]//Proceedings of ION GPS－93.Salt Lake City，UT:781－787.1993.

[6]Teunissen P J G.Least-squares estimation of the integer GPS ambiguities[C]//Invited Lecture，IAG General Meeting，Beijing，China，1993.

[7]P J G Teunissen.Success probability of integer GPS ambiguity rounding and bootstrapping[J].Journal of Geodesy，1998，72(10):606－612.

[8]P J G Teunissen.A new method for fast carrier phase ambiguity estimation[C]//Proceedings of IEEE PLANS’94.LasVegas:562 －573.1994.

[9]P J G Teunissen，P J De Jonge，C C J M Tiberius.The least-squares ambiguity decorrelation adjustment:its performance on short GPS baselines and short observation spans[J].Journal of Geodesy，1997，71(10):589－602.

[10]郑庆晖，张育林.GPS姿态测量的载波相位整周模糊度快速解算[J].航空学报，2002，23(3):272－275.

[11]陈树新，王永生.一种消除GPS模糊度相关性的新算法[J].航空学报，2002，23(6):542－546.

[12]刘立龙，文鸿雁，唐诗华.一种优化模糊度搜索方法的研究[J].海洋测绘，2006，26(1):37－39.

[13]H J Euler，H Landau.Fast GPS ambiguity resolution onthe-fly for real-time applications[C]//Proceedings of Sixth International Geodetic Symposium on Satellite Positioning，1992:650 －659.

[14]李征航，张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社，2009:28－29.

[15]李淑慧，刘经南.整周模糊度搜索方法的效率比较和分析[J].测绘通报，2003(10):1－3.