基于Matlab的三轴惯性振动筛力心解析

任 杰，侯勇俊，吴先进

（1.西南石油大学机电工程学院，成都610500；2.四川宏华石油设备有限公司，四川广汉618300） ＊

·设计计算·

基于Matlab的三轴惯性振动筛力心解析

任 杰1，2，侯勇俊1，吴先进1

（1.西南石油大学机电工程学院，成都610500；2.四川宏华石油设备有限公司，四川广汉618300）＊

在振动筛设计中，力心与质心的位置关系直接决定着振动筛的运动轨迹，因此力心的存在性及其位置确定非常重要。给出了三轴惯性振动筛力心的定义，建立了三轴惯性振动筛的简化模型，借助Matlab软件采用解析方法证明出其力心的唯一存在性，并进行了3个实例的力心位置计算。结果表明：三轴惯性振动筛有力心存在，且是唯一确定的。

三轴惯性振动筛；力心；Matlab

在现代振动筛的设计中，振动筛的激振器与筛框的相对位置决定着振动筛的振动轨迹。大量的研究表明：只要激振器产生的相对惯性力合力的作用线能够始终通过振动筛的总质心，振动筛就能够实现平动，工作过程中筛箱上各点的运动轨迹与筛箱质心的运动轨迹保持相同。因此在振动筛的设计过程中，必须知道激振器产生的相对惯性力合力作用线在运动过程中是否始终通过固定的同一点，这个点即为振动筛的力心。通过调整激振器的位置使振动筛的力心与质心重合，以便实现振动筛筛箱的平动振动轨迹。文献［1－4］提出了双轴惯性椭圆振动筛力心的概念，并证明了力心的唯一存在性。在近10a来，国内振动筛的研究［5－11］进一步发展了双轴惯性振动筛力心理论，国外采用相关理论［12］生产了一系列的双轴椭圆振动筛。三轴惯性振动筛［13］在大筛分面积的振动筛中已得到应用，其同样存在力心。目前，国内外还没有专门文献对其力心存在性和唯一性给出证明，也没有提出三轴惯性振动筛的力心计算方法。本文提出了三轴惯性振动筛力心的定义，并对力心唯一存在性进行了证明。在实际证明中，数学计算异常复杂，徒手计算困难甚至可能没有计算结果，因此本文借助Matlab软件替代人工计算，结果证明这种处理方法简单易行，效果良好。

1 力心的定义

如图1所示，惯性振动筛的激振轴1、2、3的回转中心分别为O1、O2、O3，三轴等速旋转，产生的惯性力分别为F1、F2、F3，在任意不同的t1、t2、t3时刻，F1、F2、F3的合力作用线始终通过同一固定点O，点O就是力心。三轴的回转方向可以是同向的，也可以是其中任意2个同向，另1个与之反向。

图1 三轴惯性振动筛力心定义

2 力心的唯一确定性证明

三轴惯性振动筛的筛箱和激振器简化为如图2所示的系统。其中，O1、O2、O3分别为三激振轴的回转中心；m1、m2、m3分别为三激振轴偏心质量，kg；α1、α2、α3分别为三激振轴的初始相位角，rad；r1、r2、r3分为m1、m2、m3的偏心距，mm；ω为三激振轴的旋转角速度，rad／s；L1、L2、L3分别为三轴回转中心O1、O2、O3与坐标原点O的水平距离，mm；F1、F2、F3分别为3个激振轴产生的惯性力，N，F1＝m1r1ω2、F2＝m2r2ω2、F3＝m3r3ω2。

F1、F2、F3的力作用线方程分别为

F1、F3的合力R1为

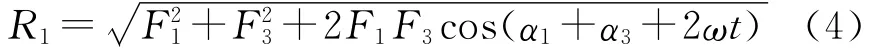
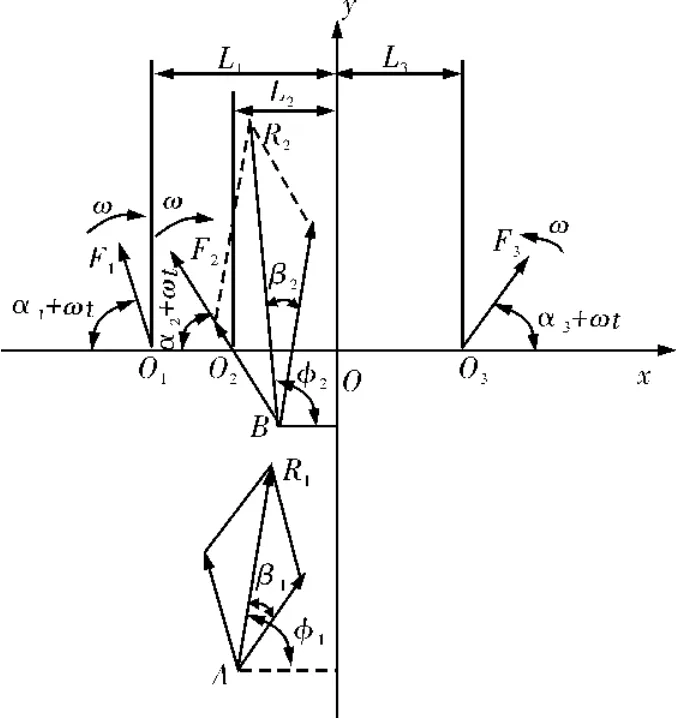
图2 三轴惯性振动筛模型简化

联立式（1）和式（3），解得F1、F3两力作用线交点的坐标xA、yA分别为

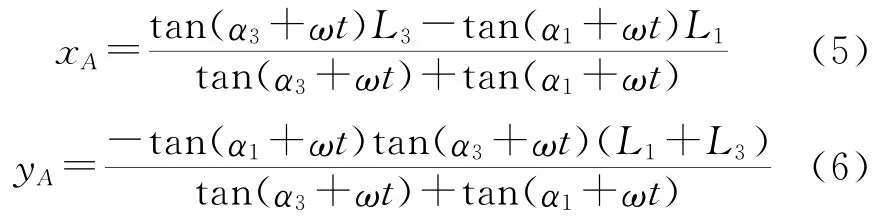
合力R1与x轴夹角为

式中，β1为合力R1与F3之间的夹角，其值为

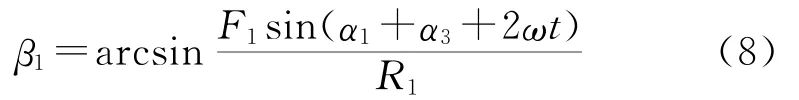
联立式（2）和式（9），解得R1、F2两力作用线交点的坐标xB、yB分别为

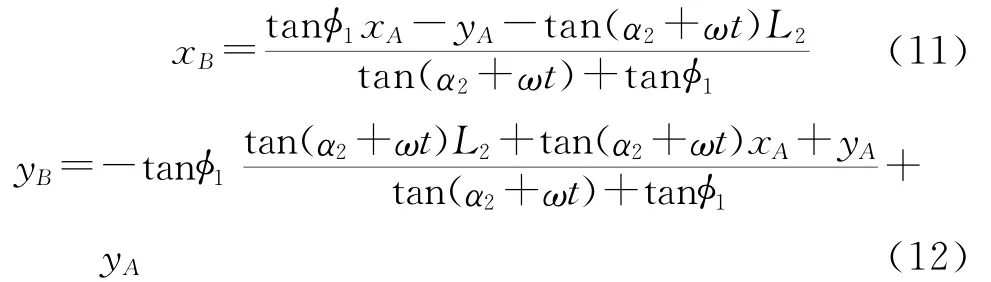
则R1的作用线方程为

R1与F2的合力R2为

合力R2与x轴夹角为

式中，β2为合力R2与R1之间的夹角，其值为

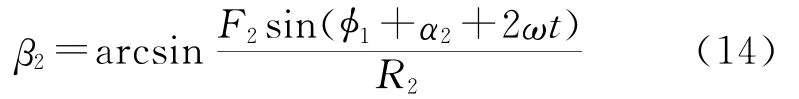
则R2的作用线方程为

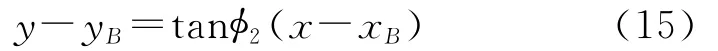
整理后R2的作用线方程变为

式（16）是一个非其次线性方程，一般形式为Ax＋ By＝C，式中A＝tan2，B＝－1，C＝tan2xB－yB，且A、B、C均是时间t的函数。在任意时刻，如果3个惯性力合力R2的作用线方程能始终通过同一点，那么这个点就是三轴惯性振动筛的力心。

在3个任意时刻t1、t2、t3有

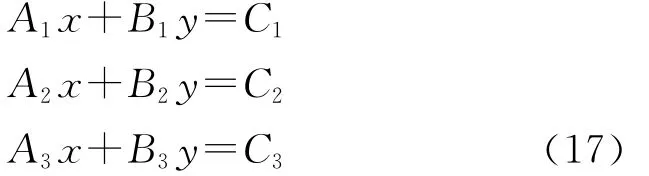
式（17）是由3个方程组成的二元非其次线性方程组，根据线性代数关于线性方程组有无解的相关知识可以知道：线性方程组有解的充分条件是＝R（S）＝r，且r＝n时，线性方程组有唯一的解［14］。其中、R（S）分别为线性方程组系数对应的增广矩阵和矩阵；n为未知数个数。式（17）中，增广矩阵由系数A1、B1、C1、A2、B2、C2、A3、B3、C3构成，矩阵由系数A1、B1、A2、B2、A3、B3构成，应用Matlab软件中的符号计算模块分别计算增广矩阵式（18）以及矩阵式（19）的秩。

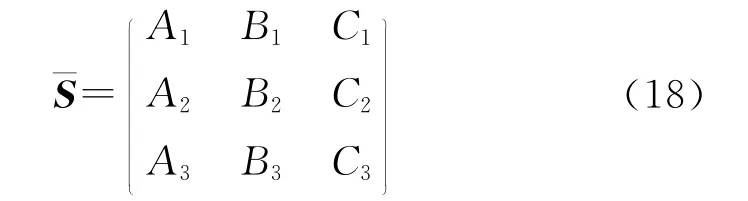
将上述公式写成相应的Matlab代码［15］（代码中符号意义与前文定义相同），并导入Matlab软件的矩阵计算模块，经过计算之后，得到增广矩阵的秩，矩阵的秩R（S）＝2，且知道线性方程组（1）的未知数个数为2，即n＝2，所以有＝r＝n＝2。这样可以知道线性方程组有唯一的解，即3个惯性力合力R2的作用线方程在任意时刻能始终通过同一点，这一点即是三轴惯性振动筛的力心，则三轴惯性振动筛的力心唯一存在。

3 力心位置计算实例

将振动筛中各参数分别赋值，可计算出不同参数时振动筛力心的具体位置（如表1）。从证明中知道，在任意t1、t2时刻，3个激振惯性力合力作用线的交点即是力心L（xL、yL），即确定性与唯一性［J］.油气田地面工程，1996，15（9）：58－60.

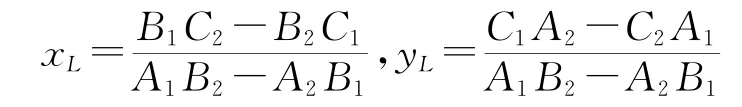
表1 力心计算实例

［4］ 马天宝.平面惯性振动筛力心的几何确定［J］.矿山机械，1996（12）：40－42.

［5］ 侯勇俊，朱维兵，游思坤，等.双轴平动椭圆振动筛设计中的两个问题［J］.矿山机械，2000（10）：46－47.

［6］ 游思坤，邓宏光.平动椭圆振动筛参数化建模［J］.石油矿场机械，2004，33（2）：34－36.

［7］ 牟长青，柴占文，朱均波，等.自同步平动椭圆振动筛的理论研究［J］.石油机械，2004，32（5）：11－12.

［8］ 任崇刚，朱维兵，舒 敏.双电机激振自同步平动椭圆钻井筛动力学分析［J］.钻采工艺，2010，33（2）：79－82.

［9］ 徐 倩，邓 嵘，李艳萍，等.2种新型钻井振动筛［J］.石油矿场机械，2010，39（8）：53－56.

［10］ 侯勇俊，曹丽娟.波浪形筛网固相运移规律研究［J］.石油矿场机械，2010，39（1）：1－4.

4 结论

本文通过解析法证明了三轴惯性振动筛的力心唯一存在，并且举例求出了3组不同参数的力心位置，得出力心位置与各参数的关系，且调整参数数值便可以调整力心。以此结论作为理论基础，在设计三轴惯性振动筛过程中只要调整力心与振动筛振动部分的质心重合，便可使振动筛的运动实现平动。

［1］ 张明洪，马天宝.钻井液平动椭圆振动筛原理［J］.天然气工业，1990，10（4）：40－47.

［2］ 张明洪，陈应华，张万福，等.双轴惯性振动筛力心与质心的计算方法［J］.石油矿场机械，1991，20（6）：7－11.

［3］ 马天宝，时宏松，张明洪.双轴惯性钻井振动筛力心的

［11］ 侯勇俊，刘 枭，冷 曦.质心偏移式等质量矩双轴振动筛运动特性研究［J］.石油矿场机械，2009，38（3）：5－9.

［12］ 王宏伟，刘 军，刘继亮.国外新型钻井振动筛研究进展［J］.石油矿场机械，2011，40（3）：72－76.

［13］ 侯勇俊，申永强，田 英，等.基于运动合成原理的三电机自同步椭圆振动筛同步稳定性研究［J］.石油矿场机械，2010，39（6）：1－5.

［14］ 何炳全，吴小庆.线性代数［M］.北京：石油工业出版社，2000.

［15］ 张琨华，靖丛滨.MATLAB7.6从入门到精通［M］.北京：电子工业出版社，2009.

Analysis of Force－center for Three－Axis Inertial Shale Shaker Based on Matlab

REN Jie1，2，HOU Yong－jun1，WU Xian－jin1
（1.School of Mechatronic Engineering，Southwest Petroleum University，Chengdu610500，China；2.Sichuan Honghua Petroleum Equipment Co.，Ltd.，Guanghan618300，China）

In the process of designing shale shaker，the ubiety between force－center and mass－center directly determined the shaker’s movement locus，therefore，it’s significance to prove the existence of force－center and where its location.First of all，concept of the force－center for Three－Axis Inertial Shale Shaker was put forward.Then，its simplified model was built up.Moreover，it proved the uniqueness and existence of this force－center by using the powerful computing tool Matlab.Finally，the center’s location within three examples was figured out by evaluating each parameter.Theory and examples both showed that the Three－Axis Inertial Shale Shaker’s forcecenter existed，and it was unique.

three－axis inertial shale shaker；force－center；Matlab

1001－3482（2012）03－0025－04

TE926

A

2011－09－20

国家自然科学基金（51074132）

任 杰（1966－），男，四川蓬溪人，高级工程师，博士研究生，主要从事石油钻井机械研究。