河道非恒定流水面线计算研究
2012-12-08褚青来河南省河口村水库工程建设管理局
□褚青来(河南省河口村水库工程建设管理局)
1.问题的提出
在工程实践中,常常要对河道、水库或渠道等的水流进行计算,以掌握其水面线和流量数据,从而为工程设计、洪水预报、水库调度、溃坝洪水演进计算等提供科学依据。对一些简单的工程,可以利用恒定均匀流计算,稍复杂的工程可以利用恒定非均匀计算,但对大型的重要工程仅靠这些计算往往不能反映实际情况,无法满足工程需要。为解决这一问题,往往要利用理论严谨、计算精度较高的非恒定流原理。
2.河道非恒定流水面线计算的基本方程
河道非恒定流水面线计算的基本方程是由水流的连续方程和运动方程组成的方程组,在假定无旁侧入流的情况下,用水位变量z和流量变量Q表示的圣维南方程组如下:

该方程组是非恒定流计算的基本方程组。由于方程组属于一阶拟线性双曲型偏微分方程,在一般情况下,无法求出其普遍的解析解,只能针对具体的明槽非恒定流问题,使用近似的计算方法求解。
3.基本方程组的解法
根据圣维南方程组的特征,结合非恒定流理论的实际应用,目前基本方程组的解法大致可分为3种:
一是特征线法。这一方法是根据偏微分方程理论,先将基本方程组变换为特征线的常微分方程组,然后对常微分方程进行离散化,再结合水流的初始条件和边界条件求解。该方法物理概念明确,数学分析严谨,计算结果精度较高,在实际计算中,其计算公式简单,容易编程。
二是直接差分法。此法是将基本方程组直接离散化,进而联解得到一组代数方程,依据离散化时采用的数值格式不同,又可将直接差分法分为显式差分法和隐式差分法。显式差分法计算简单,但限制条件较多;隐式差分法计算过程较为复杂,且仅适应缓慢水流,不适应急变流。
三是瞬时流态法,简称瞬态法。此法将运动方程中的所有惯性项忽略,从而使方程组简化为一阶非线性抛物型方程组,然后对简化方程离散化,再结合初始条件和边界条件进行近似计算。瞬态法应用较早,也是成熟有效的计算方法,但由于对基本方程组过于简化,计算精度往往不能满足实际需要。
经过上述分析,作者推荐采用特征线法求解。
4.特征线法基本方程组
特征线法的基本思想,是根据基本方程组的特点,引进一条特征线,经过推导求出特征线方程,即:
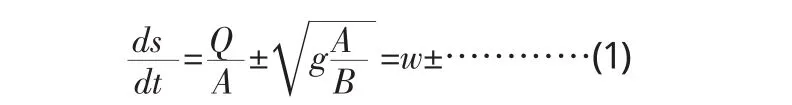
式(1)为正(顺水流方向)负(逆水流方向)两条特征方程,并经过处理得:

式(2)也为两个方程,式(1)、(2)是特征线法的四个基本常微分方程。求解这四个基本方程有很多方法,作者经过分析研究,认为库郎格式求解相对简单,计算时不需要迭代,又有一定的计算精度。
库郎格式的求解方法,首先建立矩形网格(图1),并引入积分中值定理,即:
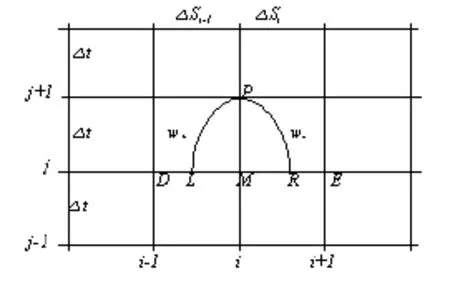
图1 矩形网格图
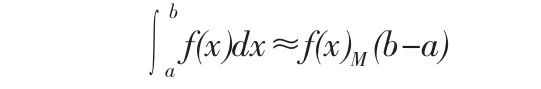
并考虑网格特点,对L点和R点进行线性内插得到L、R点的计算公式,即:
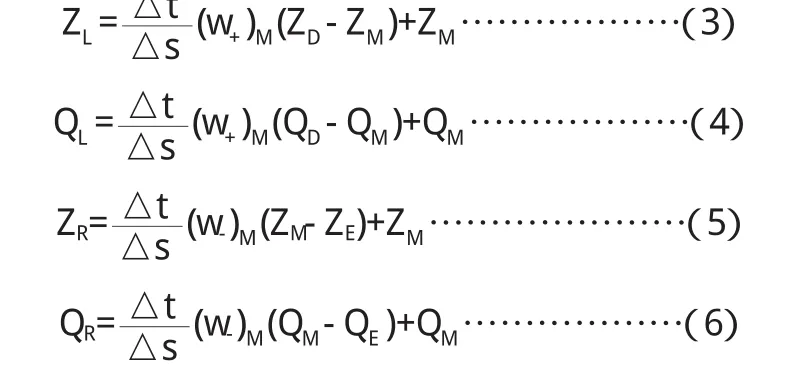
根据求得的 ZL、QL、ZR和 QR,进而可求得 ZP和 QP,即:

或

以上式中:
Z、Q分别代表水位和流量;
t为时间,△t为计算时段长;
s为顺水流方向的距离;
△s为断面间距或流段长;
D、M、E为已知网格节点;
P为求解网格节点;
L、R分别代表上、下游网格之间过渡计算点;
A为过水断面面积,B为水面宽度;
g为重力加速度,一般取9.8m/s2。
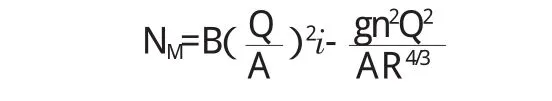
式中:B、A、Q、R、n、i分别代表 M节点水面宽度、面积、流量、水力半径和糙率、底坡。
(3)、(4)、(5)、(6)、(7)、(8)式是特征线法的库郎格式的基本方程组。该解法是利用已知的D、M、E网格节点水力要素直接计算出网格内点P点的水力要素。对于P点位于上下游边界时,则要分别情况,利用上述公式计算(详细情况在下面叙述)。
5.特征线解法的方法步骤
5.1 收集各过水断面资料
断面资料包括糙率、底坡坡降和断面几何资料。
对于糙率n,可参照有关水利设计手册选取,为保证计算精度,各断面应分别取n值,如果各断面相近也可采用统一的n值。
对于坡降,各断面应分别计算,且要把握总体坡降趋势。
对于断面几何资料,如果断面规则,比如为矩形或梯形,可直接建立高程z和面积、湿周x、水力半径R、水面宽度B之间的关系,如果不规则,如天然河道,则要根据实测资料或地形图,建立数据关系,具体求解时进行内插计算,也可将各断面的数据关系处理成关系曲线,采用近似的计算公式,以便编程。
5.2 确定计算时段、断面间距
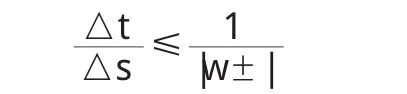
对于计算时段和流段,要依据库郎约束条件确定,即要满足关系,△s不可过大,否则影响计算精度,一般应取500m左右,特殊情况可适当放宽,但不宜超过3000m。
5.3 确定计算的初始条件
初始条件为计算起始各断面的水位和流量。非恒定流理论的前提是起始时刻各断面有一定的水深,不能是干的河道或渠道。确定起始条件时,视具体情况,可用恒定均匀流或恒定非均匀流计算各断面的水位和流量,也可根据实测资料确定水位和流量。
5.4 确定上游(入流断面)、下游(出流断面)边界条件
对上游边界条件,如果已知水位(比如从水库中引水)ZP,可直接利用式(5)、(6)和(8)计算流量 QP;如果已知流量过程线(已知 QP),将式(8)变化为:
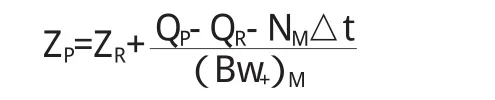
再结合式(5)、(6)计算 ZP。
对下游边界条件,如果已知水位(如下游连接大型水库、湖泊,水位稳定)ZP,可利用式(9)计算流量QP;如果已知流量(如电站引水)QP,将式(9)变换为:
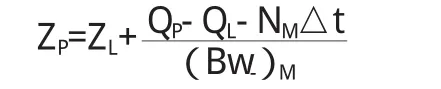
再结合式(3)、(4)计算ZP。如果下游边界为水位~流量关系即Q=f(z),如水闸,则要先利用式(3)、(4),计算出ZL、QL,然后利用式(9)和QP=f(zP)关系组成两元方程组,因一般情况无法直接解出zP、QP,要通过试算求解。
5.5 编程计算
进行非恒定流计算时,由于工作量大,要用计算机编程求解。作者结合具体的工程实例,依据非恒定流特征线法的库郎格式原理,用VB成功编制了计算程序,如有需要可同作者联系。
