基于复合形法的马铃薯分级机优化设计研究

马松柏， 白 ， 陶春生

(北京工商大学材料与机械工程学院，北京 100048)

基于复合形法的马铃薯分级机优化设计研究

(北京工商大学材料与机械工程学院，北京 100048)

分析了马铃薯分级机振动筛及物料的运动及动力学特性，从而找出其运动参数及约束条件，以复合形法结合Matlab程序设计语言对参数进行了优化求解，结果证明行之有效，可为相关产品的优化设计提供理论方法及借鉴.

复合形法;优化设计;往复直线运动振动筛;Matlab

马铃薯分级机是利用传动机构的往复直线运动使有筛孔筛面的振动速度和加速度产生周期性变化，从而筛面上物料产生相对运动，并依据物料大小、重量不同产生不同的运动距离进行分级的食品机械，其运动参数的选取至关重要.传统设计中，通过估算、经验类比或试验来确定，很难求得最佳设计参数.本文以筛分粒度为50 mm的马铃薯分级机为对象，通过合理简化建构马铃薯分级机筛面及物料往复振动运动及动力学数学模型，在保证较高筛分效率的前提下，力求提高生产率.选取往复振动面的平均推进速度为优化设计目标，借助复合形法，以Matlab为实现平台，对往复振动面的振动圆频率ω，振动振幅r，振动方向角β，振动面倾角α等参数进行了优化求解，以得到尽可能高的平均推进速度.结果表明采用复合形法取得了比传统设计更佳的设计效果.

1 往复振动面上物料相对运动的分析

设计实例要求筛分50 mm以下的马铃薯，在建立目标函数之前，分析其在振动面上的受力及相对运动状态，找出物料相对振动面的运动规律.

设振动面倾角为α，振动方向角为β，振动圆频率为ω，振动振幅为r，振动面与物料间摩擦角为φ，物料颗粒质量为m，重力加速度为g.物料沿往复振动面的相对运动主要方式如图1.

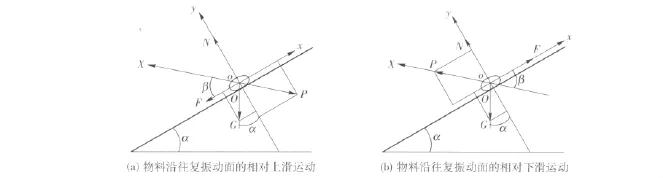
图1 物料沿往复振动面的相对主要运动Fig.1 Relative motion of potato on surface of reciprocating vibration sieve

图1中沿振动方向运动建立静坐标系OX;动坐标系为xoy，固连于振动面，x轴沿振动方向，向右为正，y轴垂直于振动方向，向上为正，则物料受力有:重力 G=mg，振动惯性力 P=mω2rsinωt，振动面支承反力N，振动面对物料的摩擦力Fmax=Ntanφ.

1.1 物料沿往复振动面的相对上滑运动

1.1.1 物料相对上滑条件［1］

如图1(a)，要使物料颗粒相对于振动面上滑，必须满足:

可得:ω2rsinωtcos(β+φ)＞gsin(φ+α).

为使上式有意义，对cos(β+φ)取绝对值，并将|sinωt|max=1代入上式，得:

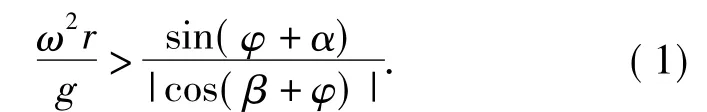
式(1)即为物料颗粒相对振动面上滑的条件.

1.1.2 物料相对上滑加速度

根据牛顿定律可得:

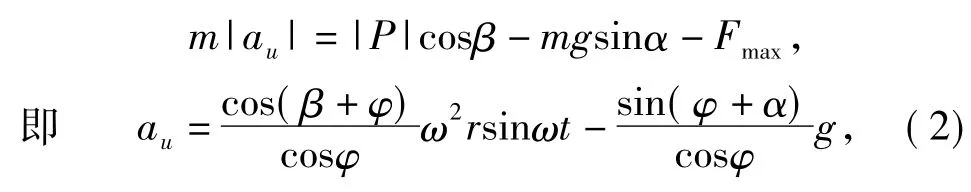
式(2)中，au为物料颗粒相对振动面的上滑加速度.

1.1.3 物料相对上滑位移

同理，由式(2)连续积分可求得相对上滑位移表达式:

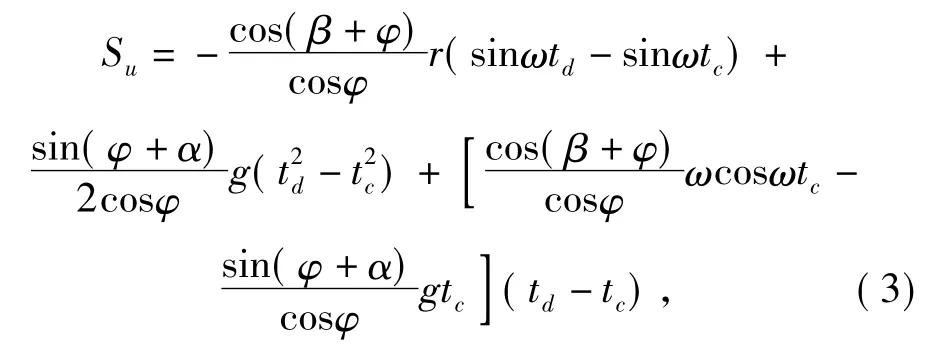
式(3)中，Su为振动面运动一个周期物料颗粒相对上滑的位移;tc为物料颗粒相对振动面开始上滑的时刻;td为物料颗粒相对振动面结束上滑的时刻.

1.2 物料沿往复振动面的相对下滑运动

1.2.1 物料相对下滑条件

如图1(b)，要使物料颗粒相对于振动面下滑，必须满足:

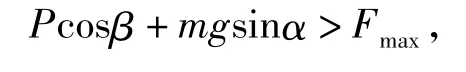
若物料颗粒相对于振动面无跳动，应有

可得:ω2rsinωtcos(β－φ)＞gsin(φ－α).

为使上式有意义，对 cos(β－φ)取绝对值，并将|sinωt|max=1代入上式，得:

式(4)即为物料颗粒相对振动面下滑的条件.

1.2.2 物料相对下滑加速度

式(5)中，ad为物料颗粒相对振动面的下滑加速度.

由式(5)连续积分求得相对下滑位移表达式:

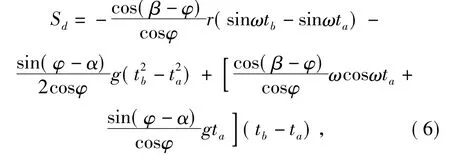
式(6)中，Sd为振动面运动一个周期物料颗粒相对下滑的位移;ta为物料颗粒相对振动面开始下滑的时刻;tb为物料颗粒相对振动面结束下滑的时刻.

1.3 物料对往复振动面的相对跳动

只有在图1(b)状态下马铃薯物料颗粒才可能相对于振动面跳动，若使物料能跳离振动面，须满足:

式(7)即为物料颗粒相对振动面跳动的条件.

1.4 物料在往复振动面上的平均推进速度

物料在振动面上仅相动无跳动时的平均推进速度应为:

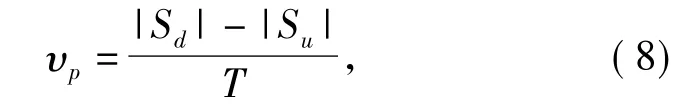
2 振动筛参数优化设计的数学模型及优化方法

2.1 设计变量

综前所述，往复振动机械的基本运动参数有:振动圆频率ω，振动振幅r，振动方向角β(振动面振动方向与振动面所夹锐角).影响物料在振动面上运动的参数还有:振动面倾角α(振动面与水平面间所夹锐角)及振动面与物料间的静滑动摩擦角φ.φ值随振动面及物料种类的确定相对为一定值，本例为马铃薯 φ，取 30°，故 ω、r、β、α 为设计变量:

2.2 目标函数

衡量以输送物料为主要目的往复振动机械工艺性能好坏的重要指标是生产率，而具有筛理作用的往复振动机械，还要求有筛分效率.生产率高低取决于物料沿振动面的平均推进速度，平均推进速度快则生产率高;筛分效率主要与物料所获振动惯性力大小及物料相对振动面的筛理行程有关.为简化优化问题，将筛分效率列入约束条件，建立单一目标函数.为了得到较高生产率应使物料沿往复振动面的平均推进速度尽可能快，目标函数即为:

2.3 约束条件

马铃薯分级机在实际生产中除应满足较高的生产率外，还应具备较高的筛分效率.因此，物料在振动面上应做双向相对运动，以增加物料与振动面接触机会及筛理行程，故物料在振动面上应具相对下滑和上滑运动，且下滑位移大于上滑位移，即:

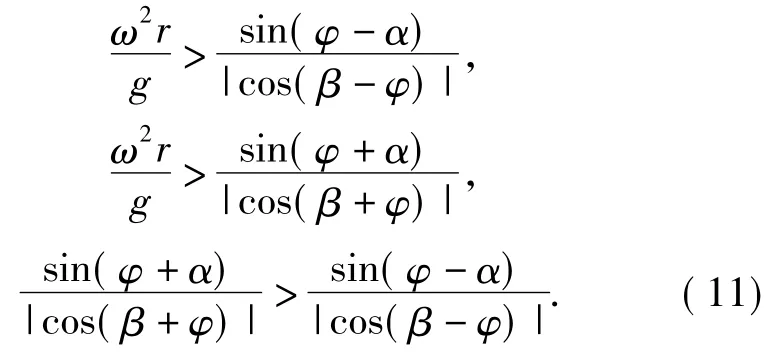
于是得约束条件为:

由于往复振动筛是利用物料自动分级性进行筛选分级的，应避免破坏物料的自动分级性，使物料相对于振动面仅滑动无跳动，且获得尽可能大的振动惯性力，即

若取两者差值不大于0.1，则约束条件为:

振动方向角β取值0°～90°，约束条件为:

振动面倾角α取值0°～5°，约束条件为:

振动圆频率ω取值41.88～62.83 rad/s(对应转速400～600 r/min)，约束条件为:

2.4 复合形法

复合形法［2－5］用于求解非线性规划问题的目标函数f(x)在多约束条件下最优解的问题，数学表达如下:

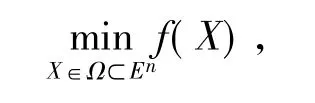
受约束于

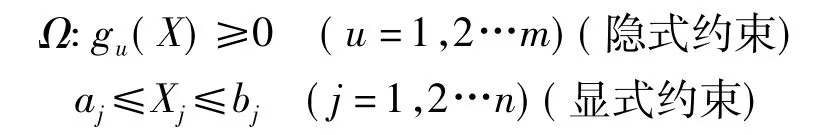
复合形法的基本思想是，先在n维空间的可行域中产生一个以k个初始点为顶点的不规则多面体的复合形，一般(n+1≤k≤2n)，然后比较复合形各顶点目标函数的大小.其中目标函数值最大的点作为坏点，以坏点之外其余各点的中心为映射中心，寻找坏点的映射点.一般说来，此映射点的目标函数值总小于坏点，也就是说映射点优于坏点.这时，以映射点替换坏点与原复合形除坏点之外其余各点构成k个顶点的新的复合形.如此反复迭代计算，在可行域中不断以目标函数值低的新点代替目标函数值最大的坏点从而构成新复合形，使复合形不断向最优点移动和收缩，直至收缩到复合形的各顶点与其形心非常接近、满足迭代精度要求为止.最后输出复合形各顶点中的目标函数值最小的顶点，作为近似最优点.

本例中目标函数为式(10)，约束条件为式g1(X)～g11(X)，即式(12)至(22)共11个约束.而由式(9)可知此为一个四维11个约束的多约束优化方法求解问题.经比较众多机械设计优化算法后，决定采用复合形算法.这是因为复合形法较为适合解决有约束优化问题，仅需比较目标函数值即可决定搜索方向，算法较简单，对目标函数的要求不苛刻，适用于变量少(小于15维)，约束条件不多的优化问题，机械优化设计中采用广泛.

3 程序实现

算法最终通过Matlab程序设计语言实现，由1个主程序和6个子程序组成，程序框图如图2.

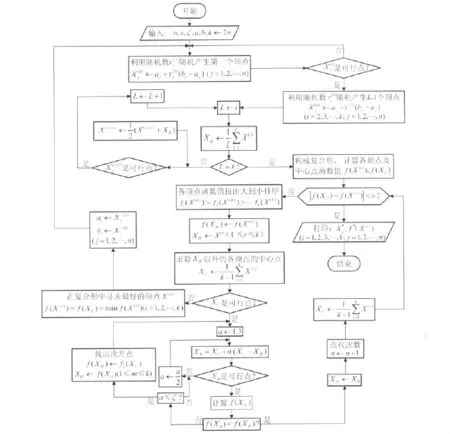
图2 复合形法程序Fig.2 Program chart of complex method

3.1 程序构成及参数说明［6－7］

主程序首先给定N，M，K值，然后定义数组维数.主程序中提供自变量的初始值，输入已知参数及打印最后结果面.

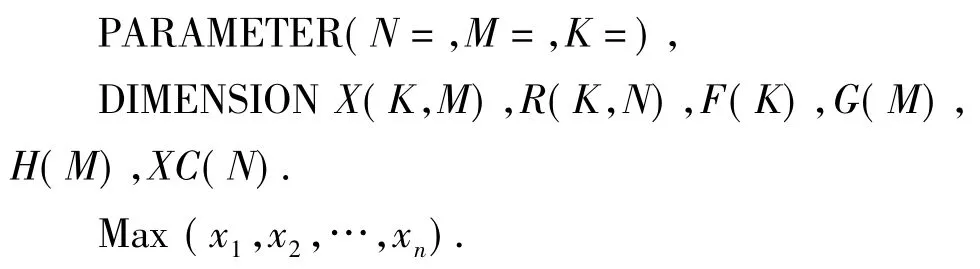
其中 x1，x2，…，xn为独立自变量，

xn+1～xm为隐式变量，是 x1，x2，…，xn的函数，Gi，Hi为下界和上界.

各子程序的作用分别为:

CONSX—是一个主要子程序，调用其他子程序及输出中间结果;CHECK—检查所有的点是否满足约束条件，对违背约束的点进行校正;CENTR—计算中心点;FUNC—目标函数;CONST—规定显式和隐式约束;RANDU—产生随机数.

1)输入参数中，N为显式自变量数;M为约束组数;K为构成复合形的顶点数，N+1;ITMAX为允许最多迭代次数;IPRINT为打印控制参数，IPRINT=1，打印中间结果，IPRINT=0，不打印中间结果;ALPHA为反射因子，常用1.3;BETA为收敛参数，函数的幅值乘1E－4;GAMMA为收敛参数，整数，常用值为5;DELTA为显式约束违反校正，小正数，如X向量幅值乘1E－4;X(1，J)为自变量初始可行点，等于1，N.

2)输出变量中，F为目标函数最大值;X(I)为自变量最优值，I=1，N.

3.2 优化结果

ω 为54.43 rad/s，约为 520 r/min;α 为3.25°约合3°;r为 4.52 mm，约为 4.5 mm;β 为 44.85°约为45°.

4 结束语

传统的食品机械设计方法已经无法满足提高生产率及经济性等诸多要求，而优化设计方法愈来愈多的得到重视和使用，本文中提到的复合形法优化设计问题在马铃薯分级机的设计中取得了较好的效果，由于该方法对目标函数的性态无特殊要求，程序设计简单，算法的收敛速度比较快，非常适合求解中小型机械的优化设计问题.

［1］梁基照.食品机械优化设计［M］.北京:化学工业出版社，2008:178-183.

［2］祝立萍，张振生，龚义书.基于复合形法的板翅式换热器优化设计［J］.安徽工业大学学报:自然科学版，2011，28(1):63-66.

［3］徐小明，蒋炎坤，刘志恩.基于复合形法的车用发动机配气机构凸轮型线设计［J］.柴油机，2007，29(6):34-36.

［4］陈惠，詹少华，阮进华.基于Matlab复合形法的二级圆柱齿轮减速器的优化设计［J］.煤矿机械，2011，32(8):31-33.

［5］韩中合，焦红瑞.基于复合形法的风力机桨叶优化设计［J］.华东电力，2009，37(9):1612-1613.

［6］王凌.智能优化算法及其应用［M］.北京:清华大学出版社，2004.

［7］王谦，赵俊利.基于Matlab软件的振动筛振动研究［J］.煤矿机械，2011，9(32):38-39.

(责任编辑:檀彩莲)

Optimal Design Research of Potatoes Classifier Based on Complex Method

MA Song-bai， BAI Qiao， TAO Chun-sheng
(School of Material and Mechanical Engineering，Beijing Technology and Business University，Beijing 100048，China)

The kinematics parameters and constraints of a typical vibrating sieve which was used as potatoes classifier were analyzed in this paper.And these parameters were optimized by complex method accomplished in the environment of Matlab software.The results proved that the complex method mentioned in this paper is an effective tool for potatoes classifier optimal design，which could offer foundation and method to design some machineries related to potatoes classifier.

complex method;optimization design;vibration sieve;Matlab

TS210.3;TS215

A

1671-1513(2012)02-0070-05

2011-11-28

北京工商大学青年基金项目资助(QNJJ2010-17).

马松柏，男，讲师，硕士，主要从事食品与包装机械设计、机电一体化技术、CAD/CAM应用等方面的研究.