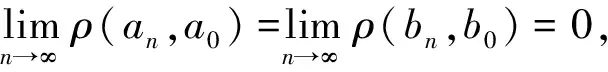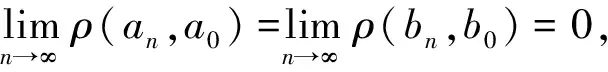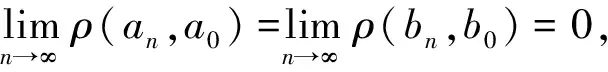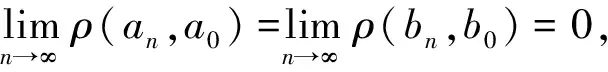基于剩余格的一类度量空间及性质

周建仁, 谢晶晶, 吴洪博

(陕西师范大学 数学与信息科学学院, 西安 710062)

0 引言与预备知识

在逻辑代数系统中, 由Pavelka[1]引入的剩余格理论是重要且应用广泛的代数系统, 如MV代数、 Boole代数、 BR0代数和MTL代数等均可视为是基于剩余格理论构成的代数理论[2-7]. 另一方面, 很多研究者考虑将Lukasiewicz和R0逻辑系统中的度量结构[7-9]引入到Boole代数、 MV代数、 R0和Godel代数等多种逻辑代数中, 并取得了许多结果[10-14]. 本文从整体上对一类逻辑代数在度量方面的性质进行研究. 先给出了剩余格上存在度量的一个充分条件及由该条件决定的该类剩余格上的度量结构; 并讨论了该种度量结构下该类剩余格中的聚点问题[13-14]; 最后证明了剩余格中的基本运算在度量空间中的连续性.

定义1[7]设P是偏序集, ⊗与→为P上的二元运算. 如果满足如下条件, 则称⊗与→互为伴随对, (⊗,→)称为P上的伴随对:

1) ⊗:P×P→P关于两个变量都是单调递增的;

2) →:P×P→P关于第一变量不增, 关于第二变量不减;

3)x⊗y≤z当且仅当x≤y→z,x,y,z∈P.

定义2[7]有界格(L,∨,∧,0,1)称为剩余格, 若其满足如下条件:

1)L上有伴随对(⊗,→);

2) 〈L,⊗〉是带单位元1的交换半群.

此时L通常记作〈L,⊗,→〉.

定理1[6]设〈L,⊗,→〉是剩余格, 则:

1)a→b=1当且仅当a≤b;

2)a→b∧c=(a→b)∧(a→c);a∨b→c=(a→c)∧(b→c);

3) 1⊗a=a;

4)a⊗b=b⊗a;

5) (a⊗b)⊗c=a⊗(b⊗c).

1 度量剩余格

定理2(剩余格上存在度量的充分条件) 设〈[0,1],⊗,→〉是剩余格. 定义二元运算ρ: [0,1]×[0,1]→[0,1]如下:

∀a,b∈[0,1],ρ(a,b)=1-(a→b)⊗(b→a).

若剩余格满足条件:

∀a,b∈[0,1],a+(a→b)≤1+b,

(1)

则ρ为[0,1]上的度量.

证明: 1) ∀a,b∈[0,1]. 首先, 由定义知ρ(a,b)≥0; 其次, 若a=b, 则(a→b)⊗(b→a)=1, 即ρ(a,b)=0. 若a

(a→b)⊗(b→a)=b→a<1,

即ρ(a,b)>0. 若a>b, 则

(a→b)⊗(b→a)=a→b<1,

即ρ(a,b)>0. 因此ρ(a,b)=0当且仅当a=b.

2)ρ(a,b)=1-(a→b)⊗(b→a)=1-(b→a)⊗(a→b)=ρ(b,a).

3) ∀a,b,c∈[0,1]. 由伴随对(⊗,→)的性质知

(a→b)⊗(b→c)≤a→c; (b→a)⊗(c→b)≤c→a.

进而结合⊗的单调性得

((a→b)⊗(b→c))⊗((b→a)⊗(c→b))≤(a→c)⊗(c→a).

由⊗的交换性、 结合性及伴随性可得

(a→b)⊗(b→a)≤((b→c)⊗(c→b))→((a→c)⊗(c→a)).

再结合剩余格〈[0,1],⊗,→〉满足的条件得

进而结合二元运算的定义得

1-(a→c)⊗(c→a)≤1-(a→b)⊗(b→a)+1-(b→c)⊗(c→b).

即ρ(a,c)≤ρ(a,b)+ρ(b,c).

综合1)～3)可知,ρ是[0,1]上的度量[15].

定义4若剩余格〈[0,1],⊗,→〉满足式(1), 则称剩余格〈[0,1],⊗,→〉为度量剩余格.

定理3设〈[0,1],⊗,→〉是度量剩余格. ∀a,b∈[0,1], 则:

证明: 1) 由定理2并结合剩余格性质可得.

2) 由伴随对性质知

a→b≤(b→0)→(a→0);b→a≤(a→0)→(b→0),

由⊗的单调性知

(a→b)⊗(b→a)≤((b→0)→(a→0))⊗((a→0)→(b→0)),

进而可得

ρ(a→0,b→0)≤ρ(a,b),

2 度量剩余格([0,1],ρ)中的拓扑性质

定理4设〈[0,1],⊗,→〉是度量剩余格,a0∈[0,1]. 则对ε>0, 存在c∈[0,1]-{a0}, 使得0<ρ(a0,c)<ε.

证明: 1) 显然∀c∈[0,1]且c≠a0,ρ(a0,c)>0成立.

2) ∀ε∈(0,1), 因为(1-ε/2)⊗a0≤(1-ε/2)→a0, 取

c∈[(1-ε/2)⊗a0, (1-ε/2)→a0]{a0}.

则有

(1-ε/2)⊗a0≤c≤(1-ε/2)→a0,

进而1-ε/2≤a0→c, 且1-ε/2≤c→a0.

当c

ρ(a0,c)=1-(a0→c)⊗(c→a0)=1-a0→c≤ε/2<ε.

当c>a0时,

ρ(a0,c)=1-c→a0≤ε/2<ε.

综合1),2)可知结论成立.

推论1在度量剩余格空间([0,1],ρ)中,∀a∈[0,1],a是聚点.

3 度量剩余格空间([0,1],ρ)上运算的连续性

证明: 由→的单调性知, ∀n∈Z+,

an→a0≤an→a0∨bn,a0→an≤a0→an∨bn.

由⊗的单调性及定理1中2)可得

进而

1-(an∨bn→a0∨bn)⊗(a0∨bn→an∨bn)≤1-(an→a0)⊗(a0→an),

即

ρ(an∨bn,a0∨bn)≤ρ(an,a0).

(2)

类似上述证明可得

ρ(a0∨bn,a0∨b0)≤ρ(bn,b0).

(3)

由式(2),(3)及

0≤ρ(an∨bn,a0∨b0)≤ρ(an∨bn,a0∨bn)+ρ(a0∨bn,a0∨b0)

可得

0≤ρ(an∨bn,a0∨b0)≤ρ(an,a0)+ρ(bn,b0),

证明: 由伴随的性质知∀n∈Z+,

b0→bn≤(an→b0)→(an→bn),bn→b0≤(an→bn)→(an→b0),

所以

(b0→bn)⊗(bn→b0)≤((an→b0)→(an→bn))⊗((an→bn)→(an→b0)),

进而

ρ(an→bn,an→b0)≤ρ(bn,b0).

(4)

类似可证

ρ(an→b0,a0→b0)≤ρ(an,a0).

(5)

由式(4),(5)及

0≤ρ(an→bn,a0→b0)≤ρ(an→bn,an→b0)+ρ(an→b0,a0→b0)

知,

0≤ρ(an→bn,a0→b0)≤ρ(an,a0)+ρ(bn,b0).

证明: 由伴随性质知∀n∈Z+,

bn→b0≤an⊗bn→an⊗b0,b0→bn≤an⊗b0→an⊗bn,

故

(bn→b0)⊗(b0→bn)≤(an⊗bn→an⊗b0)⊗(an⊗b0→an⊗bn).

进而

ρ(an⊗bn,an⊗b0)≤ρ(bn,b0).

(6)

类似可证

ρ(an⊗b0,a0⊗b0)≤ρ(an,a0).

(7)

由式(6),(7)及

0≤ρ(an⊗bn,a0⊗b0)≤ρ(an⊗bn,an⊗b0)+ρ(an⊗b0,a0⊗b0)

知,

0≤ρ(an⊗bn,a0⊗b0)≤ρ(an,a0)+ρ(bn,b0).

证明: 由→的性质知∀n∈Z+,

bn→b0≤an∧bn→b0,b0→bn≤an∧b0→bn.

由⊗的单调性及定理1中2)知

进而

ρ(an∧bn,an∧b0)≤ρ(bn,b0).

(8)

类似可证

ρ(an∧b0,a0∧b0)≤ρ(an,a0).

(9)

由式(8),(9)及

0≤ρ(an∧bn,a0∧b0)≤ρ(an∧bn,an∧b0)+ρ(an∧b0,a0∧b0)≤ρ(an,a0)+ρ(bn,b0),

[2] WANG Guo-jun. MV-Algebras, R0-Algebras, and Multiple-valued Logic [J]. Fuzzy System and Mathematics, 2002, 16(2): 1-15. (王国俊. MV-代数, BL-代数, R0代数与多值逻辑 [J]. 模糊系统与数学, 2002, 16(2): 1-15.)

[3] Esteva F, Godo L. Monoidalt-Norm-Based Logic: Towards a Logic for Left-Continuoust-Norms [J]. Fuzzy Sets and Systems, 2007, 124(3): 271-288.

[4] Esteva F, Godo L. On Complete Residuated Many-Valued Logics witht-Norm Conjunction [C]//Pro ISMVL’ 2001. Warsaw: IEEE Press, 2001.

[6] WU Hong-bo. Basis R0-Algebra and BasisL*System [J]. Advances in Mathematics, 2003, 32(5): 565-576. (吴洪博. 基础R0代数与基础L*系统 [J]. 数学进展, 2003, 32(5): 565-576.)

[7] 王国俊. 非经典数理逻辑与近似推理 [M]. 北京: 科学出版社, 2000.

[8] WANG Guo-jun, Leung Y. Integrated Semantics and Logic Metric Spaces [J]. Fuzzy Sets and Systems, 2003, 136(1): 71-91.

[9] WANG Guo-jun, ZHOU Hong-jun. Quantitative Logic [J]. Information Sciences, 2009, 179(3): 226-247.

[10] WANG Guo-jun, SONG Qing-yan, SONG Yu-jing. Metric Structures on Boolean Algebras and an Application to Propositional Logic [J]. Acta Mathematica Sinica, 2004, 47(2): 317-326. (王国俊, 宋庆燕, 宋玉靖. Boole代数上的度量结构及其在命题逻辑中的应用 [J]. 数学学报, 2004, 47(2): 317-326.)

[11] WANG Guo-jun, ZHOU Hong-jun. Metrization on MV-Algebras and Its Application in Lukasiewicz Propositional Logic [J]. Acta Mathematica Sinica: Chinese Series, 2009, 52(3): 501-514. (王国俊, 周红军. MV代数的度量化研究及其在Lukasiewicz命题逻辑中的应用 [J]. 数学学报: 中文版, 2009, 52(3): 501-514.)

[12] LI Bi-jing, WANG Guo-jun. Logic Pseudo-metric Spaces of Regular Implication Operators [J]. Acta Electronica Sinica, 2010, 38(3): 497-502. (李璧镜, 王国俊. 正则蕴涵算子所对应的逻辑伪度量空间 [J]. 电子学报, 2010, 38(3): 497-502.)

[13] DAI Jian-yun, WU Hong-bo. A Logical Structure on [0,1] [J]. Journal of Huazhong Normal University: Nat Sci, 2008, 42(2): 179-182. (代建云, 吴洪博. [0,1]上的一种度量结构 [J]. 华中师范大学学报: 自然科学版, 2008, 42(2): 179-182.)

[14] DAI Jian-yun, WU Hong-bo. Metric Structure on Logical Algebra [0,1] [J]. Computer Engineering and Applications, 2008, 44(2): 92-94. (代建云, 吴洪博. 逻辑代数[0,1]上的度量结构 [J]. 计算机工程与应用, 2008, 44(2): 92-94.)

[15] Munkres J R. 拓扑学 [M]. 熊金城, 吕杰, 谭枫, 译. 北京: 机械工业出版社, 2004.