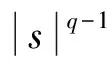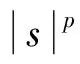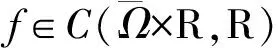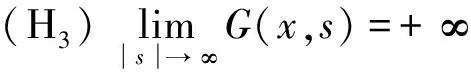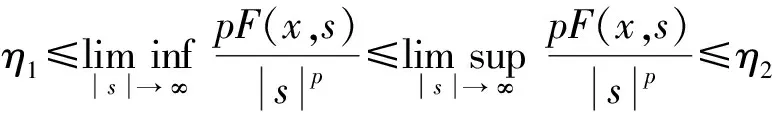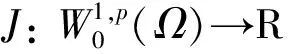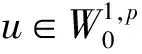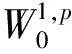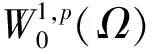一类椭圆方程解的存在性

万保成, 李 健, 李士军

(吉林农业大学 信息技术学院, 长春 130118)

考虑如下拟线性椭圆Dirichlet边值问题:

(1)

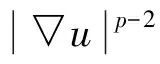
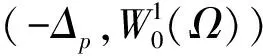
(H1) 存在C>0和q∈(p,p*)(如果1

事实上, 文献[4]在非线性项超线性增长时结合Ambrosetti-Rabinowitz(AR)条件或在渐近线性增长且在无穷远处关于λ1的共振条件满足时分别得到了一个非平凡解. 文献[5-6]在非线性项满足超线性增长但(AR)条件不满足的情形下, 结合非线性项在零点处的渐近性态, 得到了问题(1)非平凡解的存在性.

2) 当t→+∞时,J(tφ1)→-∞.

引理2在定理1的假设下, 函数J满足(C)c条件.

J(un)→c∈R, (1+‖un‖)‖J′(un)‖→0,n→+∞.

(2)

(3)

由(H4)知, 对任意的>0, 存在M3>0, 使得

(4)

令wn=un/‖un‖p, 则存在{wn}的子列(不妨仍记为{wn})及w0∈W01,p(Ω), 使得wn⇀w0, 并且wn(x)→w0(x) a.e.x∈Ω. 由式(4)可得1≤(η+). 因此, 存在Ω的正测度子集Ω0, 使得w0(x)≠0 a.e.x∈Ω0. 从而对a.e.x∈Ω0, 有un(x)→∞(n→∞). 由(H3)和Fatou引理可得这与式(3)矛盾. 因此{un}在中有界. 从而存在使得当n→∞时, ‖un‖→‖u0‖.

由引理1与引理2, 并应用推广形式的山路定理[8], 即可完成定理1的证明.

[1] Andreu F, Mazón J M, Rossi J D, et al. A Nonlocalp-Laplacian Evolution Equation with Neumann Boundary Conditions [J]. J Math Pures Appl, 2008, 90(2): 201-227.

[2] Mashiyev R A, Alisoy G, Ogras S. Solutions to Semilinearp-Laplacian Dirichlet Problem in Population Dynamics [J]. Appl Math and Mech, 2010, 31(2): 247-254.

[4] JIU Quan-sen, SU Jia-bao. Existence and Multiplicity Results for Dirichlet Problems withp-Laplacian [J]. J of Math Anal and Appl, 2003, 281(2): 587-601.

[5] FANG Fei, LIU Shi-bo. Nontrivial Solutions of Superlinearp-Laplacian Equations [J]. J of Math Anal and Appl, 2009, 351(1): 138-146.

[6] LIU Shi-bo. On Superlinear Problems without the Ambrosetti and Rabinowitz Condition [J]. Nonlinear Analysis: Theory, Methods & Application, 2010, 73(3): 788-795.

[7] OU Zeng-qi, LI Chun. Existence of Solutions for Dirichlet Problems withp-Laplacian [J]. Nonlinear Analysis: Theory, Methods & Application, 2012, 75(13): 4914-4919.

[8] Schechter M. A Variation of the Mountain Pass Lemma and Applications [J]. J London Math Soc, 1991, 44(3): 491-502.