复符号模式矩阵的复L可分性

刘 月

(福州大学 数学与计算机科学学院, 福州 350108)

0 引 言

考虑如何根据矩阵的部分信息确定矩阵的性质, 即在假设仅已知矩阵“模式”的前提下研究矩阵的秩. 实数域中研究的矩阵称为符号模式矩阵. 对于实矩阵, 此类研究一般称为实矩阵的定性分析[1-3]. 本文研究复矩阵的性质.

复矩阵A的“模式”称为A的复符号模式[4], 记为csgn(A). 设z=a+ib是一个复数, 其中a和b都是实数. 它的复符号记为csgn(z), 定义为

csgn(z)=sgn(a)+i·sgn(b).

A的复符号模式是指把A的所有元素用相应的复符号替换后所得的矩阵. 与A具有相同复符号模式矩阵全体所构成的矩阵集合称为矩阵A的复符号模式矩阵类, 记为QS(A), 即

QS(A)={Bcsgn(B)=csgn(A)}.

若一个矩阵的秩等于它的列数, 则称该矩阵是一个列满秩矩阵. 设A是一个复矩阵, 若由A的复符号模式可以推知A列满秩, 则称A是一个复L阵. 等价地,A是复L阵当且仅当A的复符号模式矩阵类QS(A)中的所有矩阵都是列满秩的. 复L矩阵的定义实质上是实数域下L矩阵定义的一种推广[2,5]. 每个L矩阵都是复L阵, 所有元素都为实数的复L阵即L阵. 方L阵即为SNS矩阵(符号非异矩阵). 非L矩阵的识别问题是NP-完全的[5].

对于方阵, 其不可约性和完全不可分性是两个基本性质, 如Perron-Frobenius定理的条件中要求矩阵是不可约的. 对于一般矩阵, 也可以定义类似的性质. 由矩阵复L性的定义可知它在行列置换下保持不变, 类似于矩阵的完全不可分性, 本文将定义复L阵的复L可分性, 该定义是L矩阵可分性的推广. 本文还将讨论复L可分性在一种特殊的矩阵变换----分裂变换[6]下的性质, 并证明矩阵的复L可分性在分裂变换下保持不变.

1 复符号模式矩阵的分裂变换及规范型

若一个复数落在复平面 C的坐标轴上, 则称其为一个轴元. 等价地, 设z=a+ib是一个复数, 其中a和b都是实数, 则当a·b=0成立时,z是一个轴元. 对任意两个轴元z1和z2, 它们属于相同的复符号模式类中当且仅当存在某个正实数k, 使得z1=k·z2. 不是轴元的复数称为象限元.

若一个复矩阵的所有元素都是轴元, 则称该矩阵是一个轴元阵. 显然, 实矩阵都是轴元阵.

在(实)符号矩阵理论向复数域推广过程中, 除复符号模式推广外, 还有另一种推广方式, 称为Ray模式推广[7-8]. 在Ray模式推广中, 非零复数z的Ray定义为z/z, 类似可以定义矩阵的Ray模式及Ray模式矩阵类. 由定义易知, 当矩阵为A轴元阵时,A的Ray模式矩阵类和复符号模式矩阵类恰好相同. 通过分裂变换, 可以把一般的复矩阵转化为轴元阵.

复矩阵的复符号非异性在分裂变换下保持不变[6], 该性质可以拓展到一般(非方)矩阵上, 并且类似可知矩阵的复L性也在分裂变换下保持不变.

定义1设A=(apq)m×n是一个复方阵,j∈〈m〉,k∈〈n〉, 其中: 〈m〉表示行指标集{1,2,…,m}; 〈n〉表示列指标集{1,2,…,n}. 假设ajk=a+ib(a,b∈R), 并且A具有如下分块形式:

其中:A12和A32是列矩阵;A21和A23是行矩阵. 记

则从A到φj,k(A)的过程称为在A的元素ajk处进行了一次分裂变换.

设A和B是两个m×n阶矩阵. 若存在两个置换矩阵P和Q, 使得B=PAQ, 则称A和B是置换相抵的, 记为A～B. 设σ=σP是P所对应的A的行指标集置换,ζ=ζQ是Q所对应的列指标集置换. 取j∈〈m〉,k∈〈n〉, 记j′=σ(j),k′=ζ(k), 设A=(ajk)m×n,B=(bjk)m×n. 则B=PAQ当且仅当ajk=bj′k′对每个j∈〈m〉,k∈〈n〉都成立. 进一步, 设j∈〈m〉,k∈〈n〉是两个给定的指标,j′,k′如前定义, 则易知φj,k(A)和φj′,k′(B)也是置换相抵的. 即对两个置换相抵的矩阵, 若在“相同”的元素上进行分裂变换, 则所得矩阵也是置换相抵的.

根据定义1, 分裂变换可以实施于矩阵的任何一个元素上. 引入分裂变换的目的之一是因为分裂变换可以减少矩阵的象限元数. 易见当对一个象限元施行分裂变换后, 所得矩阵的象限元数较原来减少1. 对象限元依次实施分裂变换, 所得矩阵是一个轴元阵. 如果固定顺序, 则最终所得矩阵是唯一的. 为方便, 本文选取字典序, 最终所得的矩阵称为原矩阵的规范型.

性质1设A是一个{m×n}阶的复矩阵, 则:

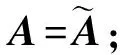
2 复L可分性及其在分裂变换下的性质

由于矩阵的复L性在行列置换下保持不变, 所以可以通过适当的行列置换, 使得所得矩阵具有相对简单的分块形式. 显然有:

定义3如果存在置换矩阵P和Q, 使得

则称复L矩阵A是复L可分的, 其中B1和B2都是非空复L阵. 若一个复L阵不是复L可分的, 则称其为复L不可分.

下面讨论矩阵的复L可分性在分裂变换实施前后的变化情况.

引理2设A是一个复L阵,ajk是A在(j,k)位置的象限元, 则A是复L可分的当且仅当φj,k(A)是复L可分的.

对于充分性, 不妨设j=k=1. 记A′=φ1,1(A), 同时记

≜B′,

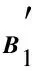
情形2) 这4个元素包含在两个相邻的块中.

(1)

或

(2)

应用引理1和引理2, 对矩阵含有的象限元个数进行归纳, 可得本文的主要结论如下:

定理1表明, 在考虑矩阵的复L可分性时, 只需把问题限制在轴元阵的范围内即可.

[1] Samuelson P A. Foundations of Economic Analysis [M]. Cambridge: Harvard University Press, 1947.

[2] Brualdi R A, Shader B L. Matrices of Sign-Solvable Linear Systems [M]. Cambridge: Cambridge University Press, 1995.

[3] Iwata S, Kakimura N. Solving Linear Programs from Sign Patterns [J]. Math Program: Ser A, 2008, 114(2): 393-418.

[4] Eschenbach C A, Hall F J, Li Z S. From Real to Complex Sign Pattern Matrices [J]. Bulletin of Australian Math Soc, 1998, 57(1): 159-172.

[5] Klee V, Lander R, Manber R. Signsolvability Revisited [J]. Linear Algebra and Its Applications, 1984, 59: 131-157.

[6] YUE Liu, SHAO Jia-yu, HE Chang-xiang. On the Boundaries of the Determinantal Regions of Ray Pattern Matrices [J]. Linear Alg Appl, 2008, 428(11/12): 2699-2707.

[7] McDonald J J, Olesky D D, Tsatsomeros M J, et al. Ray Patterns of Matrices and Nonsingularity [J]. Linear Alg Appl, 1997, 267: 359-373.

[8] Li C K, Rodman L. Inverse Closed Ray-Nonsingular Cones of Matrices [J]. Linear Alg Appl, 2005, 400: 203-230.