航天用蜂窝夹层板传热特性的研究进展

刘绍然，许忠旭，张春元，付仕明

(1.北京卫星环境工程研究所，北京100094;2.中国空间技术研究院载人航天总体部，北京100094)

1 引言

蜂窝夹层板具有重量轻，刚性大，耐疲劳性能好，导热系数小等优点，是一种有着良好的隔热、承力性能的复合材料，广泛应用在航天器承力结构、大型附件的基本结构(如太阳翼的基板、大型可展开的平面阵天线的基板等)、热防护结构的设计中，甚至有的卫星(如:美国的A2100卫星平台、中国的小卫星平台等)几乎完全由蜂窝夹层板构成卫星的主承力结构［1］。不同于一般的使用环境，航天用蜂窝夹层板的传热特性是其主要性能指标之一，它决定着蜂窝夹层板是否满足使用要求，是航天器热控设计、热变形、热疲劳和热损伤分析的重要参数。传热特性包括比热容、密度和热导率三种，对于一个固定的结构形式，前两者的等效计算方法比较简单，本文主要研究蜂窝夹层板的热导率。

本文对航天用蜂窝夹层板传热特性的国内外研究进展进行了概括和总结，主要包括:Swann-Pittman类方法、有限体积法、宏观热阻法、热叠层理论等效方法、细节有限元方法、净热流法和试验研究，对一些有待进一步研究的问题进行了展望。这些方法是分析蜂窝夹层板有效热导率的主要途径，可供航天器蜂窝夹层板材料研究和热分析者参考使用。

2 蜂窝夹层板的结构

蜂窝夹层板是一种三层的复合板，由两块上、下面板和中间的蜂窝芯子组成，通过胶黏剂或焊接把面板与芯子连接在一起，或者直接注塑或模压获得夹芯结构。面板采用强度和刚度较大的薄板材料，如铝合金、钛合金、碳纤维/环氧复合材料、凯夫拉纤维/环氧复合材料等。芯子为由很簿材料形成的蜂窝状轻质结构，采用铝合金、钛合金、芳纶纸(Nomex)材料等。

按照平面投影形状，蜂窝芯子形状有正六边形、菱形、矩形、气泡型、圆形等，其中正六边形蜂窝用料省、制造简单、结构效率最高，因而应用最广。本文也主要以芯子为正六边形的蜂窝夹层板为研究对象，其典型的结构和尺寸如图1所示。

图1 蜂窝夹层板结构分解及尺寸图

3 蜂窝夹层板传热特性的计算方法

一般来讲，蜂窝夹层板内存在着复杂传热:固体导热、辐射换热、气体导热和自然对流换热。而对于本文所探讨的范围，航天用蜂窝夹层板所在空间真空环境的特点，蜂窝结构中基本不存在气体，所以蜂窝内部的热量传递主要由热传导和热辐射的耦合作用完成，具有非线性的特点。从上面图1可以看出，由于蜂窝夹层板的芯子沿板面为正交各向异性构造，蜂窝板具有强的热各向异性，可归类为长度L，宽度W，厚度H三个方向的有效热导率(Effective Conductivity)进行研究。

蜂窝夹层板的宏观结构及芯层细观结构的传热性能研究自20世纪50年代与力学性能研究同步展开，到如今得到了充分的发展，其研究范围不断拓广，现已覆盖了夹层结构的理论分析、数值计算，试验方法，芯层的细观结构传热分析等。目前比较成熟的计算方法如下:

3.1 Swann-Pittman 类方法

Swann-Pittman方法(1961)［2］是蜂窝夹层板传热特性分析研究的经典方法，是在航空航天领域应用较为广泛的一种等效导热半经验关系式，已被作为一个标准模型用来计算蜂窝结构的热传导。在此方法中，选取一个蜂窝单元作为整个蜂窝夹层板的代表胞元进行分析，将六边形芯格与两面板构成的封闭舱间的辐射换热关系用一个等效的简单三面圆柱体模型(如图2所示)进行模拟计算。通过建立单一蜂窝单元的一维有限差分传热模型，计算芯格壁内的热传导和芯格孔内的热辐射，最后给出了适用稳态传热时计算H方向有效热导率的公式(式1)，可用于计算芯子结构随尺寸和材料参数变化时的导热系数。

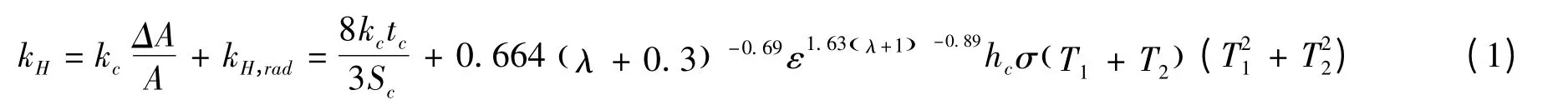
式中 kc为箔材热导率;T1和T2分别为两面板的温度;λ为三面圆柱体模型的高;hc和直径2req的比值;ε为面板和芯子的表面半球发射率。

此公式的辐射项是个经验关系式，它来自于初步的理论公式和试验数据的多次对比。从文献［2］中可以看出热辐射对有效热导率的贡献很大，并且可以近似为温度的3次方。

计算中，引入了几个简化假设:面板厚度温度均匀;芯子内部的辐射发射率是一致的并且不随温度变化;面板和芯子之间不同接触关系的影响被忽视;芯子壁和附着气体间的传热被另外考虑以便使通过芯子的传热是一维的;芯子内部的空气是不流动的以便于忽略自然对流的影响。由于这些简化，这种方法不适用于一些实际情况，在后面的介绍中可以看到对此方法进行的改进。但这些不影响它被广泛用于蜂窝夹层板设计时，预计有效热导率。

Elam［3］(1965)采用类似S-P方法的一维瞬态公式计算了蜂窝夹层板的瞬态传热特性，在这里芯子的热导率是随温度变化的。从结果看出，在两面板温差△T＜100 K时，分析值和试验值的相符程度很差。

Fatemi等［4］(2009)提出用辐射换热系数(杰勃哈特因子)计算蜂窝芯子内的辐射传热，在分析H方向传热时，对蜂窝单元采用相等横截面积的方法简化为等效的圆柱体模型，用于替代S–P方法。这种方法的优点在于:可考虑面板和芯子采用不同材料的情况，拓宽了适用范围。

此方法在H、L、W方向的芯子有效热导率以下式计算:

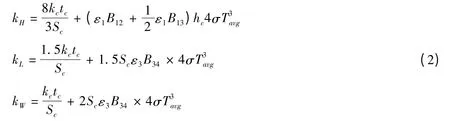
图2 等效圆柱体表面

如果考虑面板的热阻，上述公式中的导热项可变为下式［5］:

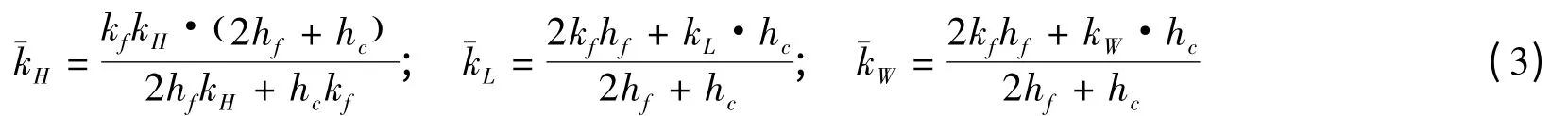
式中 Tavg为芯子的温度;kf为面板热导率。

通过上述分析可见，这类数学分析方法都是选取一个蜂窝单元作为研究对象，在分析H方向的传热时，等效简化为三面圆柱体模型。对于通过芯子的热传导，根据结构特点，利用傅立叶定律和热阻并串联规律建立模型;对于芯格内的热辐射，则采用基于辐射换热系数的辐射近似计算方法或者半经验公式建立模型。这类方法具有公式简洁、使用方便的忧点，利于工程应用，但是由于建立在大量简化假设的基础上，导致局限性大，比如在文献［6］显示，在300－500 K范围内，试验测量数据和S-P方法的计算值之间的误差高达17% ～61%;另外这类方法不适于用来预计蜂窝夹层板的瞬态传热特性。

3.2 有限体积法

Kamran在文献［6］(2001)中基于和S-P方法相似的假设，但等效的圆柱体模型是采用相等横截面周长的方法进行简化，后者的半径是正六边形外接圆半径。同时考虑了面板和胶粘层的热导率，在二维圆柱坐标系下，用有限体积法研究了蜂窝板内辐射导热耦合有效热导率。由于分析过程比较冗长，这里不具体讨论，仅列出控制方程。对于一个单元控制体(如图3所示)，其一维传热控制方程为式4。采用改进的Newton-Raphon法计算建立的非线性方程组。

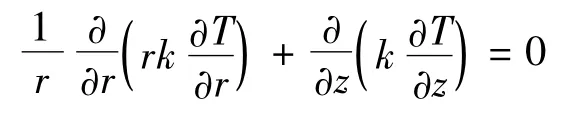
图3 蜂窝芯子结构示意图

对于控制体内的辐射换热计算，采用净热流法:

式中 N为每个控制体的表面数目。

李东辉等［7］(2008)也用有限体积法对一个蜂窝单元进行传热分析，但采用蒙特卡洛法计算控制方程的辐射换热源项。分析结果表明，对所研究的蜂窝结构，在750 K以上蜂窝芯子内表面辐射换热成为热量主要传递方式。减小芯子内表面发射率可明显减弱表面间辐射换热，是降低高温下蜂窝有效导热系数的有效途径。

和S-P类方法一样，这种数值计算方法也是选取一个蜂窝单元作为研究对象，但是视为单元控制体，把描述传热现象的微分方程组通过离散化改写成代数方程组，通过迭代法、消元法、矩阵法等用计算机计算出结果，对于芯格内的热辐射，则采用基于净热流法或蒙特卡洛法进行计算。这种方法的计算精度较高，比如Kamran方法的计算结果和试验数据的差值仅为1.7±5.9%。

3.3 宏观热阻法

文献［8－9］和文献［10］在不考虑辐射传热的作用下，采用热阻分析方法，得出低温下蜂窝夹芯板三个方向的有效热导率分别为:

式中 Af、Ae、Aad分别为垂直于热流方向面板、芯子箔材和胶黏剂的截面积;ΔXf、ΔXe、ΔXad分别为热流方向面板、芯子箔材和胶黏剂的传热距离;N为宽度内箔材条数;A为蜂窝夹芯结构的截面积;ΔX为热流方向传热的距离。

这种方法是采用热阻并串联的规律从宏观角度进行的数学分析，公式简单实用，但是仅考虑的热传导，而忽略了热辐射的作用，误差比较大。在设计不同热导率的蜂窝夹层板时可采用这种方法，根据不同温度下的箔材、胶和面板热导率数据，近似估算蜂窝夹层板的低温热导率。

3.4 热叠层理论等效方法

热叠层理论(Thermal Lamination theory simulation)起初用于复合材料的力学性能分析，Rolfes［11］首先提出了类似一阶剪切变形理论的线性热叠层理论，对复合材料层合结构进行分层简化，与有限元方法结合用于一维稳态热分析，后来［12］(1991)又提出了二次方程热叠层理论用于瞬态问题。文献［13］中用基于这两种方法建立的二维有限元模型(QUADLLT［14］和QUADQLT［15］)与三维有限元模型进行了比较，可看出两者的相符性很好，并且二维模型更有效和快捷，在进行热分析时大大减少了工作量。但这些研究是对一般的复合材料叠层结构的分析，没有特别针对蜂窝夹层结构进行研究，因此这些方法并不十分适用于对复合材料蜂窝夹层结构非线性瞬态热传导的计算。

文献［16］等在一般的热叠层理论基础上，根据蜂窝夹层复合材料结构整体来看分层较少、并且两侧面板厚度与芯层厚度相差很大的特点，作出了一些不同于一般复合材料层合结构的假设，如结构温度分布及温度梯度分布连续的假设、减弱面板与芯层之间物性变化影响的假设和传热时蜂窝结构是主体成分的假设，而根据这些假设来改进热叠层理论得到的方法更接近蜂窝夹层结构的实际。在此假设基础上，将结构在中面(对称面)上划分为有限个平面单元，用每个单元的热传导控制方程和边界条件组成一个非线性方程组，即可用于蜂窝夹层板一维瞬态温度场分析的有限元数学模型。文中算例表明:蜂窝夹层复合材料结构热物性参数(热传导率、对流换热系数和比热容)随温度变化的非线性热传导，对蜂窝夹层板的热传导有显著影响，只有非线性程度很小时忽略非线性因素导致的误差才可被忽略。

这种将热叠层理论和有限元方法相结合求解传热系数的方法，与三维有限元或有限差分计算模型相比具有计算效率高的优点，但是将芯层作为一个连续的整体，没有考虑蜂窝夹层板L、W两方向的传热，仅能计算H方向的有效热导率，这是此方法的缺陷。此外，对这种方法的计算结果精确度还需要进一步的研究。

3.5 细节有限元模型

随着计算机性能的提高，基于成熟专用或通用软件的有限元建模技术日趋成熟，对蜂窝板的实际结构进行细节建模成为可能，可以直接按实体蜂窝结构进行有限元计算。Chamis和Aiello等在文献［17］中用MSC/NASTRAN软件分别建立了芯子详细建模和等效均匀简化的蜂窝夹层结构三维有限元模型，分别如图4和图5所示。前者的蜂窝芯子在厚度方向用三层单元模拟，后者用四层实体单元模拟，在进行等效时使用了叠层理论。从计算结果来看，前者的模拟精度更高。

在Copenhaver［18］建立的沿厚度方向的一维传热有限元模型中，对面板应用了集中参数法，将其视为温度均匀的一个单元;将芯格壁沿高度均分为十个单元;考虑了蜂窝芯子内辐射传热的影响，使用蒙特卡洛法计算各个辐射单元节点的角系数，每个芯格壁单元发射10 000 000个粒子，面板按面积比例发射粒子数。同时，文中建立了基于非线性最小二乘法，包含数学模型仿真结果和试验测量数据的目标函数，在最小化目标函数的过程中寻找最忧的未知热特性值。用于最小化目标函数的是补偿函数方法(Penalty function method)，而 Dowding等［19］和 Hanuska等［20］分别用的是高斯线性化方法(Gauss linearization method)和遗传算法(Genetic Algorithms)。

图4 三维有限元模型(蜂窝芯子详细建模)

图5 三维有限元模型(蜂窝芯子等效均匀简化)

这种利用分析软件直接建立细节的有限元模型，相较于前面的解析法，具有运算效率高、计算结果准确、更改参数方便的优点，但是建模工作量大。比较适用于蜂窝结构的优化设计、与试验结合的准确求解或者同步计算机械性能等情况。

3.6 净热流法

唐羽烨等［21］(2005)从无限大蜂窝夹芯板中选取周期性的胞元结构作为研究对象，一个细观胞元刚好包含一个完整的蜂窝结构，建立其有效热导率求解方程式6和三维有限元模型(如图6所示)，通过给定第二类边界条件(两面板稳定的热流)和芯子内的辐射边界条件，分析其温度梯度与外加热流的关系，得到单层模型以及三层模型各层沿层厚的宏观热导率。

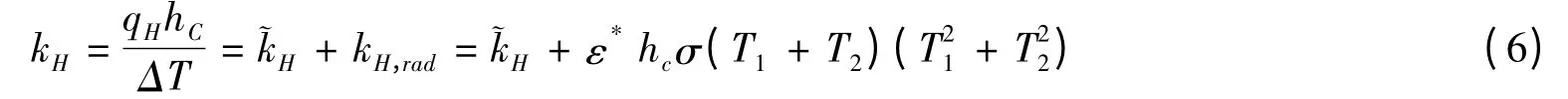
式中珓kH为不考虑内部辐射时的导热系数;ε*折算的层间辐射系数。

与S-P法比较了有效热导率的计算结果，指出后者存在误差的原因是面板内表面各处温度不均匀，与芯格壁距离较远的大部分区域上下面板的温差大于芯格壁温差;同时指出当芯层温度水平较高时，芯层内部辐射换热是不能忽略的。

文献［22］采用的方法与文献［21］类似，但给定的边界条件为第一类边界条件(两面板外表面上节点的温度)，给出了有效热导率随蜂窝板上平均温度变化的变化曲线。

这种方法是在基于总体能量平衡和层间热流连续的假设上列出能量关系式，再根据细观有限元模型计算的温度场求得有效热导率，因此引入了有限元模型的误差，最终结果的精度有待试验验证。但是直观地根据能量流动建立描述传热现象的数学模型，对于一些简单的传热问题还是比较准确的，也许可以应用在L和W两方向上。

3.7 基于试验的传热特性建模方法

为了更准确地获得蜂窝夹层板的传热特性，或者在建立蜂窝夹层板传热数学模型后，对模型中的参数进行计算以及模型的验证，通常采用试验的方法，这种试验可以说是建模的另一工作。由于蜂窝夹层板受环境、材料和制作工艺的影响较大，需要精心的设计和实施，才能准确地进行试验。此外，由于与金属材料相比，复合材料性能数据的分散性往往较大，因此，较高的测试技术和测量精度才能保证试验的有效性。下面介绍几种典型的试验装置。

Stroud［23］(1965)在670 K至1 050 K的范围内测量了四块铜焊全金属蜂窝夹层板的有效热导率，结果显示，测量数据和S-P方法的计算值之间的均方根误差仅为7%。试验装置如图7所示。

图6 单个胞元的有限元模型

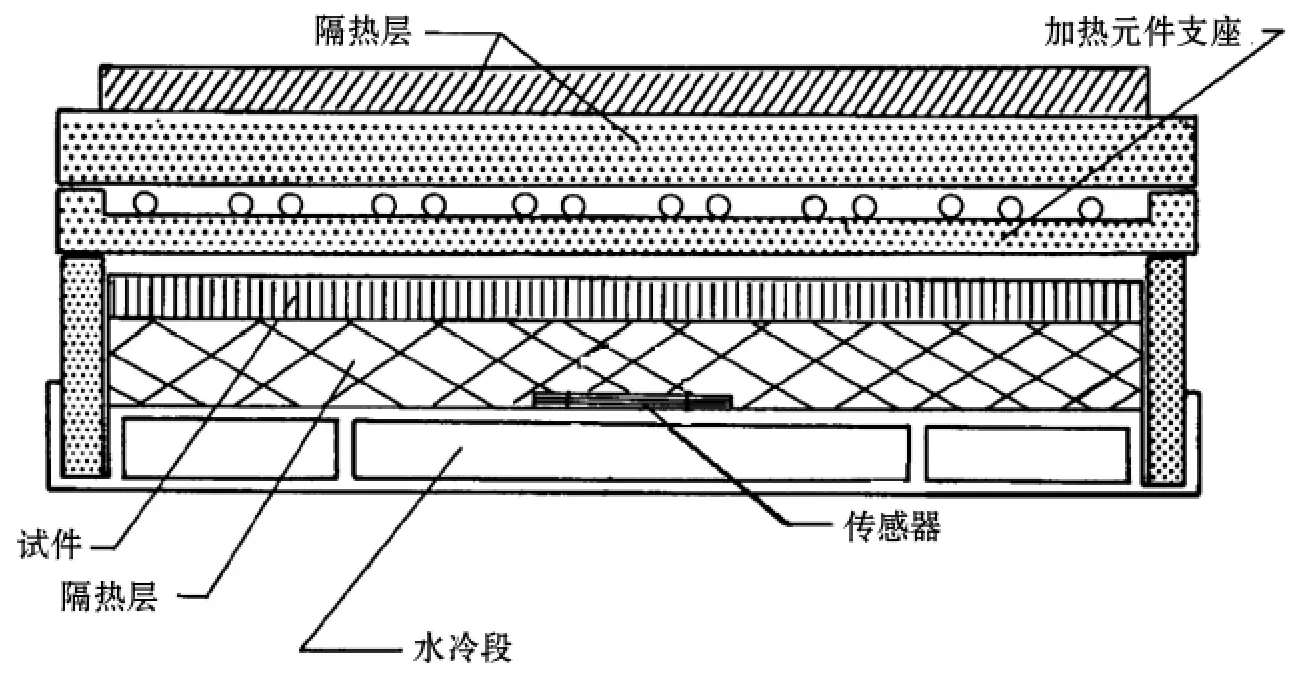
图7 Stroud试验装置示意图

Kevin D.Cole［24］(1998)继承了文献［18］中的试验装置，如图8所示，这种装置提高了热参数温度响应的敏感性，可用于瞬态试验，测量蜂窝夹层结构热特性。文献［24］中，用非线性回归方法比较了瞬态试验数据和瞬态一维瞬态有限差分模型，得出有效热导率。一维(H方向)瞬态传热方程如下:

式中 kc'为通过芯子壁的导热热导和通过芯子腔体的辐射热导之和;T0为初始温度;边界条件为q1(τ)(施加在顶部面板的瞬态热流)和T2(τ)(底部面板瞬变温度)。

由于底部面板的瞬变温度作为一个边界条件，将底部面板和芯子之间的接触热阻与芯子热阻合并考虑，接触热阻视为零，底部面板和芯子有共同的热流和温度。

上面的传热模型用有限差分法进行计算。最后的有效热导率可用式3计算，式中的kH为此处的kc'。文中同时计算并讨论了在蜂窝夹层结构热特性研究中对面板使用集中参数法的条件，即有着相对高重量、高热导率的面板和低重量、低热导率的芯子，在这种情况下，首先面板厚度相对芯子厚度可以忽略，另外面板的热导率远远高于其余结构的热导率，这样相对于整个蜂窝结构，热量可以很快扩散到整个面板。

图8 瞬态试验装置示意图

C.L.Yeh等(2001)［25］用的测量铝蜂窝夹层板热导率的试验装置示意图如图9所示，试验中，辅助加热器和主加热器保持相同的温度，以减少轴向漏热。在文献［26］中给出了较为详细的测试与分析方法。

图9 C.L.Yeh试验装置示意图

国内关于蜂窝板的热导率方面的试验研究还有兰州物理研究所的张建可等，对H方向试样，采用双平板低温热导率测定装置［27］(1981)。对L、W两个方向的试样，采用浮动热沉固体材料低温热导率测定装置［28］(1987)，测试不确定度小于 10%。

4 结束语

为了实际求解航天用蜂窝夹层板的传热问题，可以采用许多不同的几何模型(包括对象为蜂窝单元或者整体结构)和不同的分析方法。目前已有多种多样比较成熟的方法，包括从方程解析解到有限元数值解;从一般解析方法到统计方法;从理论公式到经验公式，等等。这些方法都有两个最基本的假设:(1)忽略自然对流的影响;(2)辐射面的全灰度假设。

有效热导率分析的正确性在很大程度上取决于数学模型(包括几何模型和节点、网格划分的精细程度)的建立。由于实际蜂窝夹层板的复杂性，存在芯格大小和分布的不均匀性、芯层与面板之间的脱胶等等。所以，要建立精确模拟实际情形的数学模型几乎是不可能的。同时，引入的假设越少，数学模型愈精确，则分析方法也愈复杂，在实际使用上非常困难。到目前为止，上述列举的多数分析方法和计算公式在结果上能与试验结果很好符合，但有些方法过于复杂或有很大局限性，在使用的时候要根据具体情况选用。

为满足工程上的迫切要求，应将蜂窝夹层板传热特性的建模和分析，与蜂窝夹层板的设计结合起来，因此传热特性的研究具有很强的工程实用价值。本文根据空间应用的特殊性，对蜂窝夹层板的传热特性的研究进展进行了综述。并通过分析，归纳了已有研究成果中尚待完善之处，概括起来，以下两个方面仍有待进一步的探索:

(1)要关注在使用过程中瞬态环境变化对蜂窝夹层板的影响，即材料物性参数随温度变化的情况，发展一种更为有效的求解方法。

(2)考虑空间应用特有的约束条件，针对蜂窝夹层板的传热特性，进行全面、系统的试验研究，并进行合理的试验数据分析，尤其是不同方向和多变量传热的试验建模。

［1］陈烈民.航天器结构与机构［M］.北京:中国科学技术出版社，2005.

［2］Swann，R.T.，Pittman，C.M.，Analysis of Effective Thermal Conductivities of Honeycomb-Core and Corrugated-Core Sandwich Panels，NASA TN D-714，NASA Langley Research，1961.4.

［3］Elam，B.F.，"Heat Transfer in Honeycomb-Core Sandwich Panels，"ASME paper 65－HT-13，presented at the ASME-ALCHE Heat Transfer Conference，Los Angeles CA，1965.

［4］J.Fatemi，and M.H.J.Lemmen，Effective Thermal Mechanical Properties of Honeycomb Core Panels for Hot Structure Applications［J］.JOURNAL OF SPACECRAFT AND ROCKETS:2009，546(3).

［5］Jin Zhangli，Sunil C J.Thermal Control Schemes for a Micro-Satellite with All-Active and Selectively Active Solar String Designs［J］.Heat Transfer Engineering:2006，27(10):80 ～89.

［6］Kamran Daryabeigi.Heat Transfer in Adhesively Bonded Honeycomb Core Panels.AIAA 2001-2825.NASA Langley Research Center Hampton，VA.35th AIAA Thermophysics Conference.2001，6.

［7］李东辉，夏新林.金属蜂窝结构的稳态热性能［J］.工程热物理学报，2008，29(12):2094～2096.

［8］张建可.铝蜂窝复合材料x、y方向低温有效热导率的测试与研究［J］.宇航学报，1991(1).

［9］张建可，冀可夫.碳纤维面板铝蜂窝夹层结构低温热导率测试研究［J］.真空与低温，2003，9(1).

［10］石芳录，朱贤.蜂窝夹芯结构有效热导率分析模型的建立［J］.低温工程，1993(1).

［11］Rolfes R.Efficient Thermal Analysis of Anisotropic Composite Plates Using New Finite Elements.in:Füller，J.;Grüninger，G.;Schulte，K.;Bunsell，A.R.;Massiah，A.:Developments in the Science and Technology of Composite Materials，Proceedings of the Fourth European Conference on Composite Materials(ECCM4)，Stuttgart.1990:743 ～748.

［12］Rolfes，R.:Higher Order Theory and Finite Element for Heat Conduction in Composites，in:Lewis，R.W.;Chin，J.H.;Homsy，G.M.:Numerical Methods in Thermal Problems，Vol.VII，Proceedings of the Seventh International Conference，Stanford，U.S.A.，1991:880 ～889.

［13］J.Tessmer，R.Rolfes.2D Thermal Analysis of Hybrid Composite Structures.http://www.smr.ch/local/workshop/2000/papers/dlr/tessmer.pdf.

［14］Sipetov，V.S;Karpilovskii，V.S;Demchuk，O.N.:Application of the Finite Element Method to Solve the Stationary Heat Conduction Problem of Piecewise Inhomogeneous Systems.In:J Eng Phys 55，Nr.6，1989:1439 ～1443.

［15］Noack，J.;Rolfes，R.:Efficient thermal analysis of hot structures using new finite elements.Proceedings European Conference on Spacecraft Structure，Materials and Mechanical Testing，Braunschweig，Germany，pp.117 ～121，1998.

［16］邱志平，林强.蜂窝夹层复合材料结构非线性传热分析［J］.复合材料学报，2005，22(5):147～154.

［17］C.C.Chamis，R.A.Aiello，P.L.N.Murthy.Fiber Composite Sandwich Thermo structural Behavior:Computational Simulation［C］//AIAA，ASME，ASCE，AHS.27th Structures，Structural Dynamics，and Materials Conference(SDM).San Antonio:1986.

［18］D.C.Copenhaver，E.P.Scott，A.Hanuska.Thermal Characterization of Honeycomb Core Sandwich Structures［J］.JOURNAL OF SPACECRAFT AND ROCKETS:1998，7，35(4):539 ～545.

［19］Dowding，K.J.，Beck，J.V.，Ulbrich，A.，and Hayes，J.Estimation of Thermal Properties and Surface Heat Flux in Carbon-Carbon Composites［J］.Journal of Thermophysicsand Heat Transfer:1995，9(2):345 ～351.

［20］A.Hanuska，E.I.Dupont，E.P.Scott，etc.Thermal Characterization of Complex Aerospace Structures［C］//37th AIAA Aerospace Sciences Meeting and Exhibit.Reno，NV，1999，1

［21］唐羽烨，薛明德.蜂窝夹芯板的热学与力学特性分析［J］.复合材料学报，2005，22(2):130－136.

［22］卢小艳，鲁华平，高宗战.航天器蜂窝结构的传热计算［J］.机械设计制造，2008，3:47～49.

［23］C.W.Stroud.Experimental Verification of an Analytical Determination of Overall Thermal Conductivity of Honeycomb-Core Panels.NASA Technical Note D-2866，1965，6.

［24］Kevin D.Cole，Thermal properties of honeycomb panels－analysis of transient experiments with one-dimensional models.HTD-vol.361-5，Proceedings of the ASME Heat Transfer Divison，1998.

［25］C.L.Yeh，C.Y.Wen，Y.F.Chen，S.H.Yeh，C.H.Wu，An experimental investigation of thermal contact conductance across bolted joints，Exp.Thermal Fluid Sci.2001，25(6):349 ～357.

［26］C.L.Yeh ，Y.F.Chen，C.Y.Wen，K.T.Li.Measurement of thermal contact resistance of aluminum honeycombs.Experimental Thermal and Fluid Science:2003，27:271 ～281

［27］朱贤，冀勇夫，张建可等.绝热材料低温热导率测定方法研究［J］.低温物理，1981，(4):334－339.

［28］张建可.浮动热沉式固体材料低温热导仪［J］.低温工程，1987，(1):1～6.