带时依协变量的重复测量资料的混合线性模型分析及其MIXED过程实现*
2012-12-04上海交通大学医学院生物统计学教研室200025张莉娜
上海交通大学医学院生物统计学教研室(200025) 张莉娜
重复测量资料是对同一观察对象的同一观察指标在不同时间点上进行的多次测量。其特点是存在时间上的自相关性。基于似然函数法原理的混合线性模型弱化了常规设计方法所要求的独立性假定,是一般线性模型的扩展,允许资料存在某种相关性以及协方差矩阵的多样性,从而更好地适应重复测量资料的特点。
在重复测量设计中,除了由设计者所施加的处理因素外,还可能考虑到影响反应变量的非处理因素,即协变量。协变量有两种,一种是受试者在试验开始前就有的,称固定协变量或受试者别协变量;另一种协变量随时间变化而变化,称为时依协变量。
本文通过一个临床试验实例来对带时依协变量的重复测量资料进行混合线性模型分析,并给出MIXED的过程实现。
资 料
为了研究某新药治疗轻、中度原发性高血压的疗效和安全性,以坐位舒张压为主要疗效指标,采用随机、多中心、阳性药物平行对照、双盲双模拟临床试验,收集234例轻、中度原发性高血压患者随机分到1,2两组,分别采用对照药和试验药。所有符合试验方案、依从性良好、试验期间未服用禁止用药、完成CRF的病例纳入PP(per protocol)分析集,由于无效而提前退出的病例也纳入PP分析。本试验的疗效分析用PP分析。
给药方案:疗程总计10周,两组均按导入期(2周)和治疗期(8周)进行。给药途径为口服。受试者每天于早餐后(8时左右)服药。导入期每日1次、每次试验和对照药的安慰剂各1片;治疗期头2周每日1次、每次服试验或对照药及其模拟片各1片。若2、4、6周其中一个周末血压≥140/90 mmHg,增加至每次各2片(仍为每日1次),直至总疗程8周结束。
分别在治疗前、治疗2周、治疗4周、治疗6周、治疗8周5个时间点记录每个受试者的坐位舒张压和用药量,数据结构见表1。

表1 带时依协变量的重复测量资料数据结构
方 法
混合线性模型(mixed linear model)
记第i例受试者在时间点j(j=1,…,p)的反应变量观察值为yij,协变量观察值为zij,则数据集表示为[(yi1,zi1)(yi2,zi2),…,(yip,zip)],i=1,…,n
给定符号Y为反应变量矩阵,X为设计矩阵,Z为时依协变量矩阵。建立线性关系式

式中β为固定效应的参数矩阵,γ为时依协变量的参数矩阵,其主对角线元素为 γjj,(j=1,…,p)、非主对角线元素为0。下标为矩阵维数。展开式为:

其中等式右边的第一部分是设计效应,中间部分是时依协变量效应。γ11是第1个时间点的时依协变量 Z1=(z1p,z21,…,zn1)'的参数,γpp是第 p 个时间点的时依协变量 Zp=(z1p,z21,…,znp)'的参数。
在混合线性模型中,应用最大似然法或约束最大似然法和最小方差二次无偏估计对参数进行估计。
比起一般线性模型,混合线性模型的优势在于假定协方差具有某种形式的结构,既不会像单变量分析方法那样严格,也不会像多变量方差分析那样对协方差矩阵完全无约束,从而更好地适应重复测量资料的特点。而选择正确的协方差结构将影响固定效应参数估计值的准确性,尤其是影响其标准误的计算,所以是拟合该混合模型时最关键的一步,本文给出几种常用的协方差矩阵以备选用。

of order 1[AR(1)]


软件实现
利用SAS 9.1中的MIXED过程来实现带时依协变量的重复测量资料混合线性模型拟合与参数估计。no表示受试者编号,group表示分组(1=对照组,2=试验组),time表示不同重测时间点,以各时间点坐位舒张压的下降值为反应变量,各时间点用药量的改变值为时依协变量拟合模型。SAS程序如下:


结果讨论
协方差结构的选择可以通过似然比统计量(-2Log Likelihood)、Akaike'Information Criterion(AIC)、Schwart's Bayesian Criterion(BIC)来判断,其中主要是AIC和BIC,这两个统计量的值越小说明模型拟合得越好,从而选取相应的协方差结构。在统计量的值相近时,则选取含参数个数最少的一个。
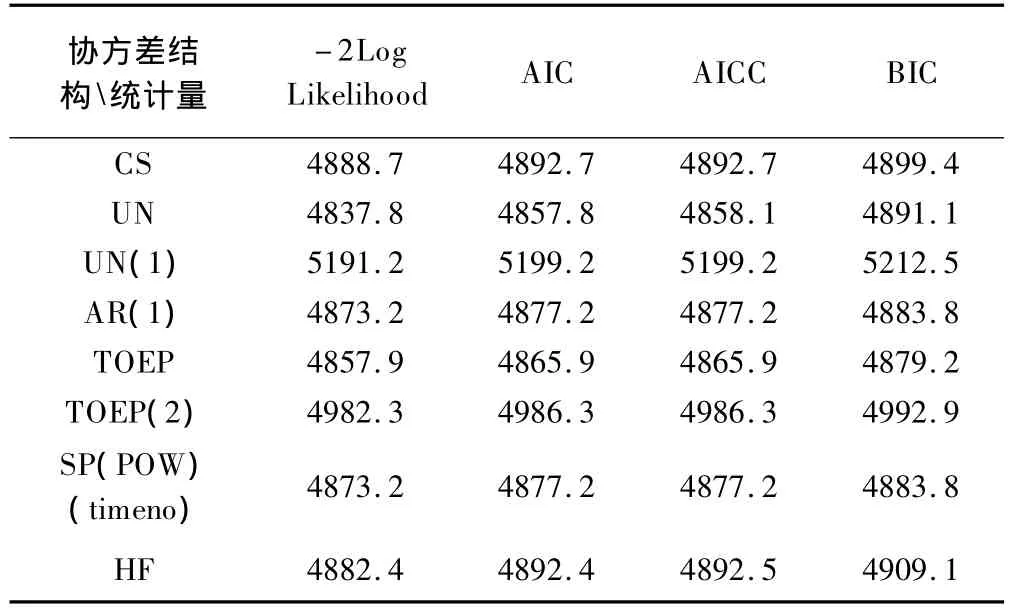
表2 不同协方差结构下的各种拟合优度检验统计量
表2列出了不同协方差结构下的各种拟合优度检验统计量,经过综合比较,选取无结构型协方差矩阵(UN)。
模型的最大似然检验:χ2=355.88,P <0.0001。说明无结构型协方差矩阵要优于普通常方差的最小二乘估计,模型拟合效果显著。

表3 固定效应的3型检验
表3结果显示:两组平均坐位舒张压下降值的差别无统计学意义(P=0.4475),即两种药对治疗轻、中度原发性高血压病的疗效无差别;各时间点之间差异有统计学意义(P<0.0001);分组效应与时间效应的交互作用无统计学意义(P=0.1523),说明试验组和对照组的坐位舒张压下降值随时间变化趋势的差别无统计学意义;协变量×时间交互效应有统计学意义(P=0.0481),说明各时间点的用药方案对降压疗效的影响有显著效应;协变量×分组交互效应有统计学意义(P=0.0075),说明两种药的用药方案对降压疗效的影响有显著效应;时依协变量有统计学意义(P=0.0061),即给药方案对治疗轻、中度原发性高血压病有显著效应。
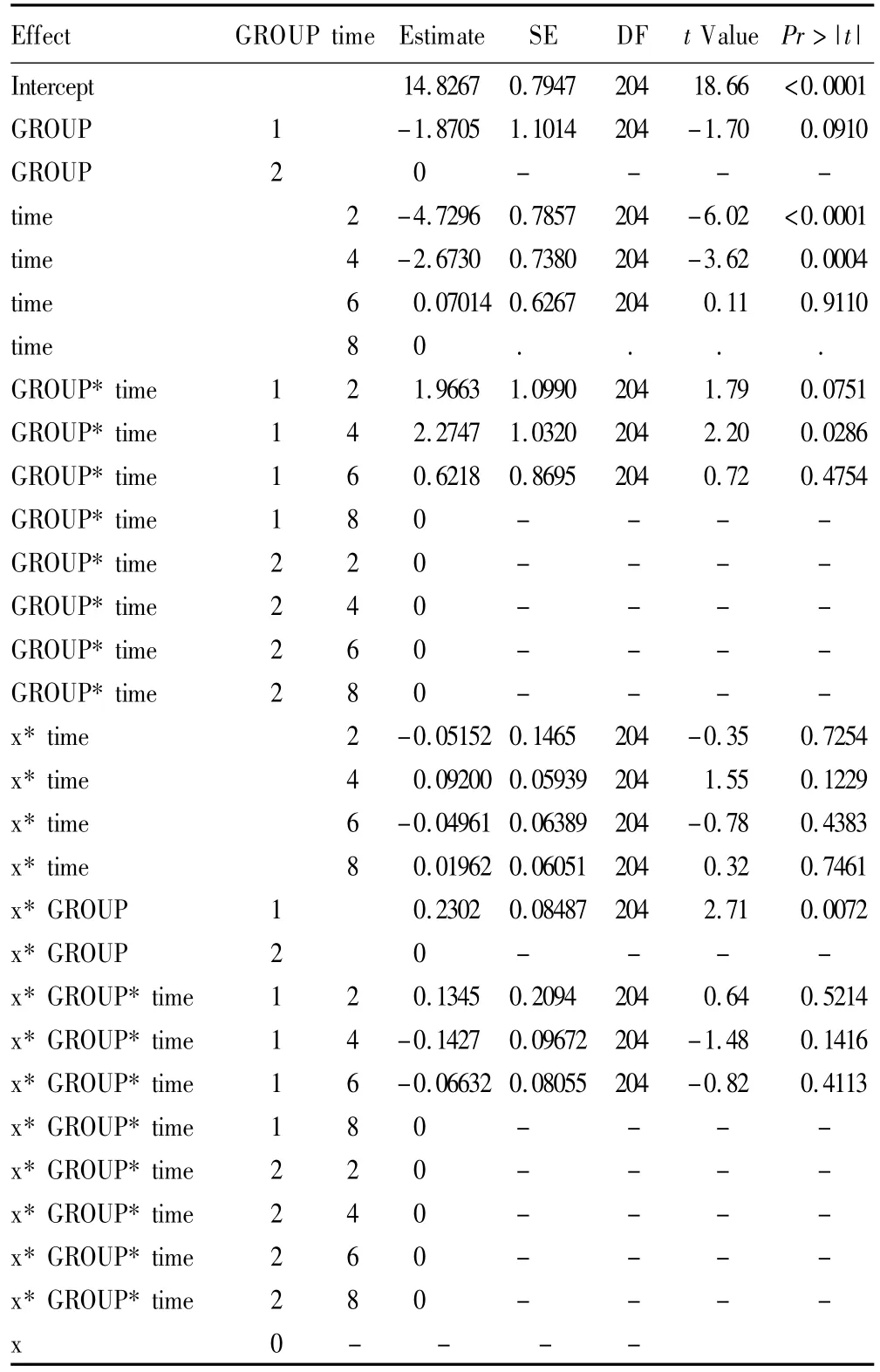
表4 固定效应的参数估计值
表4结果显示:试验组相比对照组对坐位舒张压下降值的影响为正效应,P=0.091接近显著性水平,第8周相比第2周、第4周对坐位舒张压下降值的影响为正效应,P值均小于0.05,第8周相比第6周对坐位舒张压下降值的影响无统计学意义,对照组相比试验组给药方案对坐位舒张压下降值的影响为正效应,P=0.0072。

表5 各时间点的两两比较
表5结果显示:第6周和第8周无统计学差异,其余各时间点都有统计学差异。
表6结果显示各组在各时间点上的坐位舒张压下降值修正均数、标准误、95%的可信区间。
图1从直观上提示试验组在各时间点的坐位舒张压下降值的增长幅度略大于对照组。
总之,药物临床试验大多需要定期收集病例数据,在统计策略上应该首先考虑混合模型。

表6 经x校正后两组在各时间点的平均坐位舒张压下降值
混合线性模型中提供的多种协方差结构,在数据之间相关性较为复杂时,能够更好地拟合数据之间存在的相关性,更适合于带时依协变量的重复测量资料。SAS中的MIXED过程能充分挖掘数据信息,揭示其内在特点并给出合理的统计结论。
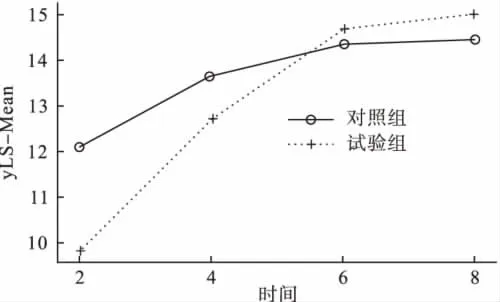
图1 两组坐位舒张压下降值的修正均数在各时间点的比较
1.Helen Brown,Robin Prescott.Applied Mixed Model in Medicine.Chichester:John Wiley & SonsLtd,1999,199-259.
2.Littell RC,Miliken GA,Stroup WW,et al.SAS for Mixed Models.Second dition.Cary,NC,USA:SAS Institute Inc,2006:174-177.
3.Khattree R,Naik DN.Applied Multivariate Statistics with SAS Software.Second Edition.Cary,NC,USA:SAS Institute Inc,1999:278-287.
4.施红英,沈毅.混合模型在临床试验重复测量资料中的应用.中国卫生统计,2007,24(2):140-142.
5.高萌,张强.方差分析和混合线性模型在重复测量数据中的应用探讨.现代预防医学,2008,35(7):1221-1223.
6.余松林,向惠云,编著.重复测量资料分析方法与SAS程序.北京:科学出版社,2004,3.
7.高惠璇编译.SAS系统SAS/STAT软件使用手册.北京:中国统计出版社,1995,4.
