常用二阶段抽样方法的评价
2012-12-04复旦大学公共卫生学院卫生统计教研室公共卫生安全教育部重点实验室200032陈文锋赵耐青
复旦大学公共卫生学院卫生统计教研室公共卫生安全教育部重点实验室(200032) 陈文锋 赵耐青 朱 敏
在流行病学调查研究中,经常采用二阶段抽样方法来获取样本。当我们面对的总体个体数很庞大,而且分布范围很广时,如果使用单阶段抽样方法,则不仅工作量大,而且在精度上很难把握。此时可以考虑采用二阶段抽样方法,这样就能够避免上述困难。比如说,我们要评价某省15岁以上人群的脉压差情况,可以从该地区100个县中抽取6个县,每个县抽取300个个体进行脉压差调查。根据实际情况,各个阶段可以采用不同的抽样方法。
在抽取样本时,需要考虑两个问题,一个是抽取到的样本的代表性,一个是抽取样本的可行性。当在一个比较大的范围内抽取样本时,抽取到的样本代表性比较好,但是可行性差;当在一个比较小的范围内抽取样本时,抽取到的样本代表性比较差,但是可行性比较好。我们需要在兼顾可行性和代表性的情况下来选择抽取样本的方法,而在流行病学调查研究中,通常有三种常用的方法来抽取样本,即随机抽样、根据先验信息在中心位置抽样以及方便抽样。随机抽样代表性最好,但是可行性差;方便抽样可行性好,但是代表性最差;根据先验信息在中心位置抽样的可行性和代表性介于其他两种方法之间。
由于不同县的15岁以上人群的平均脉压差存在某些差异,因此对于第一阶段以县为抽样单位的抽样而言,存在抽样变异(表现为各个县之间的平均脉压差的差异)。第二阶段需要在抽取到的县里面抽取个体,而这些个体也存在随机变异。因此在二阶段抽样中存在两种随机变异:各个县之间的平均脉压差的随机变异和每个县内个体间的随机变异。本文建立了二阶段抽样的模型,并用随机模拟的办法比较了这三种抽样方法的优劣性,为以后能够正确地使用这些抽样方法提供了依据。
原理和方法
1.模拟二阶段抽样方法的模型
第一阶段从目标人群中抽取若干个县;第二阶段再从第一阶段抽取到的每个县内随机抽取相同个体组成样本。假设总共抽取到m个县,每个县内抽取n个个体,第i个县内的第j个个体Xij服从正态分布Xij~N(μi,σ2)。考虑到群内聚集性,假设 μi,i=1,2,…,m不全相等,并且 μi~ N(μ0,τ2)。那么 Xij可以表示为

其中ei~ N(0,τ2),δij~ N(0,σ2),i=1,2,…,m;j=1,2,…,n。
并且假定随机变量ei和随机变量δij是独立的。
2.二阶段抽样方法的评价指标

可以证明上述两个参数估计分别是τ2和σ2的无偏估计,则X=的标准误为
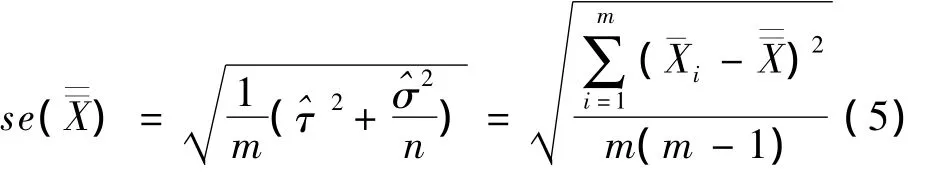

总体均数μ0的置信区间为简单随机抽样的95%置信区间公式为

以估计出来的置信区间包含总体均数的覆盖率做为评价指标,来比较这三种抽样方法的优劣。
3.模拟实验的设计
假定研究人群分布在100个县(N=100),每个县内15岁及以上的人口数在4 500至5 500的范围内。以不同地区不同文化程度的15岁及以上人群平均脉压差为研究背景,设置研究人群的脉压差平均数(总体均数μ0)为50,设第i个县15岁及以上对象的脉压差均数为μi=μ0+ei,ei为第i个县脉压差均数的第一阶段抽样误差,假定ei~ N(0,τ2),第i个县第j个对象的脉压差观察值Xij=μ0+ei+δij,δij为个体抽样误差,假定δij~N(0,σ2)。本研究分别考察在100个县中抽取6和25个县(m=6和25),设置县与县之间变异的标准差τ=0.5、3、4和10(mmHg),个体变异的标准差σ=3、4和10的随机模拟结果。在每个县内随机抽取300个个体进行研究。在每种设置下进行100次模拟实验,以每次模拟得到的95% 置信区间是否包含总体均值作为评价指标,整个实验用SAS语言编程进行模拟。
结果与分析
本文模拟三种抽样方法,分别重复模拟100次,每种抽样方法分别得到100个样本并计算95%置信区间,统计这些置信区间包含总体均数μ0的覆盖率。

表1 第一阶段抽6个县,比较三种抽样方法,两种估计的95%置信区间覆盖率(%)
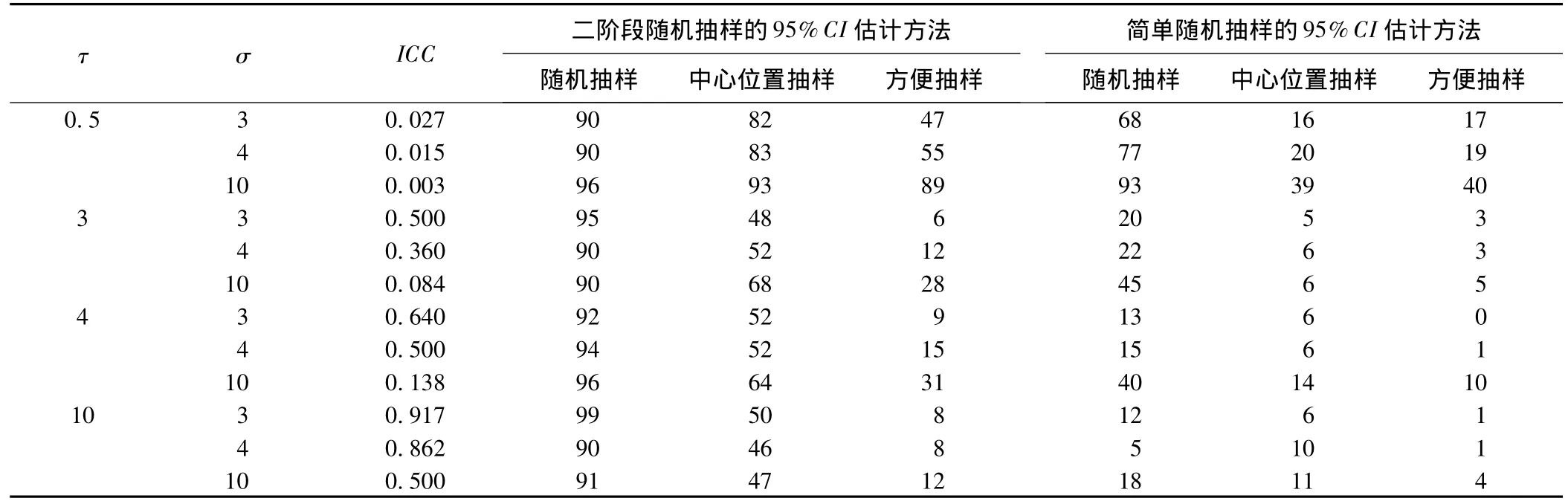
表2 第一阶段抽25个县,比较三种抽样方法,两种估计的95%置信区间覆盖率(%)

表3 随机抽样选取县和在中心位置抽样选取县等价的情况及P值
1.各种方法的优劣性
在抽取县个数不小于6时,用随机抽样方法选取县得出的置信区间包含总体均数的覆盖率是最大的,而方便抽样选取县得出的置信区间包含总体均数的覆盖率是最小的。经卡方检验,三种选取方法不等效,随机抽样选取县的效果最好,根据先验信息在中心位置抽样选取县次之,而方便抽样选取县的效果最差。
2.各种抽样方法的95%置信区间覆盖次数关于参数τ和σ的回归模型
以随机抽样选取县得到的95%置信区间不覆盖总体均值μ0的次数为应变量,以参数τ和σ为自变量,建立Poisson回归模型进行分析。参数τ和σ对随机抽样选取县得到的置信区间不覆盖总体均值μ0次数的影响没有统计学意义。
以中心位置抽样选取县得到的95%置信区间不覆盖总体均值μ0的次数y为应变量,以参数τ和σ为自变量,建立Poisson回归模型,得到回归方程为

可见此种抽样方法得到的置信区间不覆盖总体均值的次数随着参数τ的增加而上升(系数^β1的假设检验统计量为=59.37,P <0.0001);随着参数σ的增加而下降(系数^β2的假设检验统计量为W=
以方便抽样选取县得到的95%置信区间覆盖总体均值μ0的次数y*为应变量,以参数τ和σ为自变量,建立Poisson回归模型,得到回归方程为

可见此种抽样方法得到的置信区间覆盖总体均值的次数随着参数τ的增加而下降(系数^β1估计的假设检验统计量为=170,P <0.0001);随着参数σ的增加而上升(系数^β2估计的假设检验统计量为W
3.各种方法的两两比较
方便抽样选取县的方法和其他两种抽样方法相比对总体参数μ0的估计效果不等价。而随机抽样选取县和在中心位置抽样选取县相比在参数τ比较大时不等价,从表3可以知道在 σ≥3,τ=0.5,即 ICC≤0.027时这两种方法是等价的。
4.置信区间的计算方法
从表1、表2可以知道,首先利用三种抽样方法下得到样本数据,然后利用二阶段随机抽样的95%CI估计方法和用简单随机抽样的95%CI估计方法计算置信区间。结果显示,这两种方法计算出的置信区间对总体均数的覆盖率不同,差别都具有统计学意义。这种具有层次结构的数据用二阶段随机抽样的95%CI估计方法要比简单随机抽样的95%CI估计方法有效。
讨 论
在快速流行病学评估中常采用二阶段抽样方法。根据本文对常用的三种抽取县的方法在各种情况下的比较发现,随机抽样选取县的方法其效果都是最好的,只是其可行性差,因此在条件允许的情况下应该尽量选取此抽样方法。而方便抽样选取县的方法其效果在大多数情况下都是最差的,尽管此方法可行性好,但一般不建议将其作为选取县的方法。
根据先验信息在中心位置抽样选取县的方法,和随机抽样选取县的方法对总体参数μ0的估计有着相似的效果。但是只有在σ比较大,而τ比较小时,比如σ≥3,τ=0.5时,两者才等价。如果有先验信息,并且先验信息中参数σ和τ满足此条件时,本文建议用在中心位置抽样选取县来代替随机抽样选取县。
群体总体参数μ0所处的水平对估计的效果没有影响,因此在实际应用时不需要考虑μ0所处的水平。
1.付鹏钰,胡东生,顾东风.多阶段整群随机抽样方法在流行病学研究中的运用.中国卫生统计,2010,27(3):299-300.
2.杨珉.多元分析的发展—多水平模型简介.中国卫生统计,1994,11(5):32-35.
3.汪嘉冈.SAS V8基础教程.北京:中国统计出版社,2003:544-554.
4.金水高.中国居民营养与健康状况调查报告之十:2002中国居民营养与健康状况数据集.北京:人民卫生出版社,2008:251-253.
