基于可变库存费和短缺费的变质性物品的库存模型

贾 宁，陶 胜，杨志林

（合肥工业大学 数学学院，安徽 合肥230009）

近几十年来，随着计算技术和计算机应用技术的不断普及，库存控制模型的应用越来越广泛。许多学者致力于变质性物品的生产与销售的库存模型的研究，之前的大多经典库存模型均假设单位时间单位物品的库存费和短缺费是常数。然而，在实际中，并非所有物品的单位时间单位物品的库存费和短缺费是常数，如某贵重物品的储存和短缺时这些费用也会随着时间的增加而增加，后来，许多学者研究了库存费和短缺费是时间函数的库存模型。1982年，Weiss［1］较早地研究了库存费为非线性时变函数的库存问题；1994年，M Goh.［2］进一步分析了单位物品库存费与库存量呈非线性关系的库存问题；2001年，毛晓丽［3-4］在Goh的基础上建立了单位库存费可变的变质物品EOQ模型，但未考虑短缺现象；2007年，Mark Ferguson等［5］提出的库存模型也认为单位库存费与时间有关，并结合实际进行了运用，得到一些有价值的结论；2007年，Benkherouf等［6］建立了一种单位库存费和缺货费用均为线性时变函数的库存模型。这些都是涉及库存费和缺货费用可变的库存模型，但都未考虑变化问题，且都是假设订货费是固定不变的，然而一般订货费用应包括以下2个部分；一部分是差旅费、通讯费等，这部分费用可认为是固定不变的；另一部分是所订物品的运输费、装卸费等，这部分费用则是与订货量有关的可变费用，本文在订货费用是可变的假设下，分别建立了库存费和短缺费均是时间的函数及库存费是库存量的函数的2个库存模型，并且从理论上给出了其最优解。

1 模型的记号与假设

（1）系统运行在无限计划期内，前置期为零，瞬时补货，补货量不受限制，在此过程中生产厂家无折扣活动。允许短缺发生，且短缺量完全延期供给。

（2）Q1表示一个周期内系统的最大库存水平，Q2表示一个周期内系统的最大短缺水平，而Q为每个周期的订货量，即Q＝Q1＋Q2。

（3）t1表示一个周期内库存量降为0的时刻，T是一个订货周期长度。

（4）p表示单位商品的进货价格，Ar表示每次订货费用，且Ar＝A＋cQ，其中c表示单位订货的附加费用。

（5）D表示常数需求率；产品的变质率α是假定是一个常数，且商品变质后无残值。

（6）HC表示一个周期的库存费；SC表示一个周期的短缺费；PC表示一个周期的进货成本；DC表示一个周期的订货费；TC表示库存系统的平均费用。

2 基于库存费用和短缺费用为时间的函数的库存模型

在实际中，并非所有物品的单位时间单位物品的库存费和短缺费是常数，如某贵重物品的储存和短缺时这些费用也会随着时间的增加而增加，针对这些情形可假设库存费HC和短缺费用SC满足下列方程：

其中h1（t），s1（t-t1）和h′1（t），s′1（t-t1）在t∈（0，＋∞）上均大于0。由以上假设可知，设I（t）为t时刻的库存水平，则I（t）应满足下列方程：

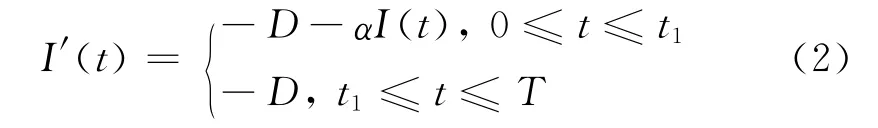
且I（t1）＝0，则得

则一个订货周期内最大库存量Q1＝I（0）＝D（eαt1-1）／α，最大短缺量为Q2＝I（T）＝D（T-t1）即每个周期的订货量为Q＝Q1＋Q2＝D（eαt1-1）／α＋D（T-t1）。

若系统从t＝0开始运行，则一个周期［0，T］内的费用由以下几个部分组成：

（1）库存费

（2）短缺费

（3）订货成本

（4）订货费用

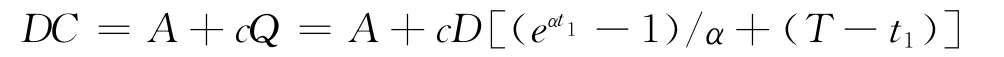
则一个周期［0，T］内的库存系统的平均费用为

下面问题是确定两个决策变量t，T的最优值，使得系统的平均费用TC最小，即求解如下的最优问题：

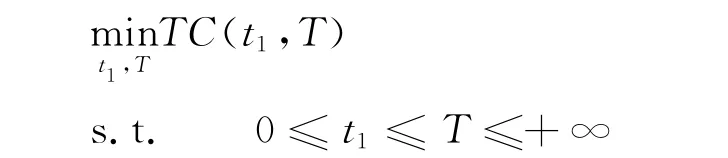
由函数的极小值必要条件知，T和t1的最优值应满足下列方程

由分析可得出以下结论：

定理1 上述方程组（5）、（6）存在唯一的一组解。

证明可令（6）式左边为

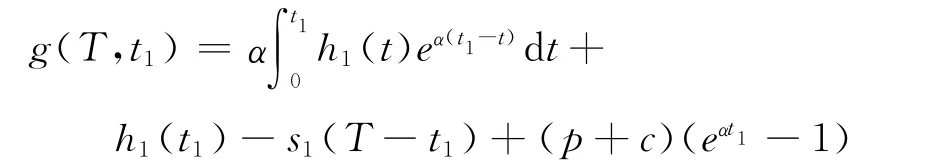
则

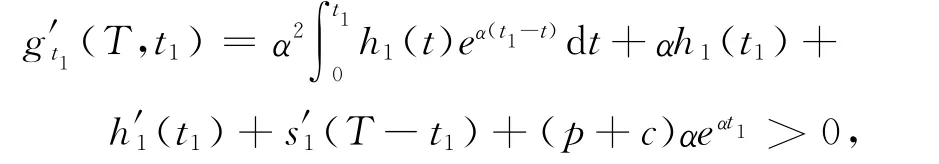
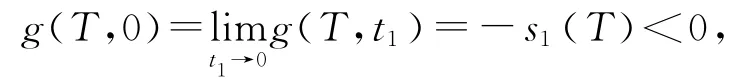
定理2 上述方程组的唯一的一组解（T＊，t＊1）使得平均费用函数TC达到最小值。

证明由于

则有

所以TC在（T＊，t＊1）处的海森矩阵正定。故（T＊，t＊1）是TC的整体唯一的最小值点。

3 基于库存费为库存量的函数的库存模型

在现实生活中，库存费用和短缺费用一般是可变情形的，且这些物品的价值一般较高，为了减少物品的变质或因随时间的增加而产生库存费和短缺费的损失，人们就需要采取一些措施来使其总费用最少。可假设此模型下单位时间单位物品短缺费用为s是常量，库存费HC满足方程dHC／dt＝h2（I）且h2（I）＞0在（0，＋∞）内可导，即

而

所以库存费

短缺费

其余费用同2中的模型，则系统的平均费用

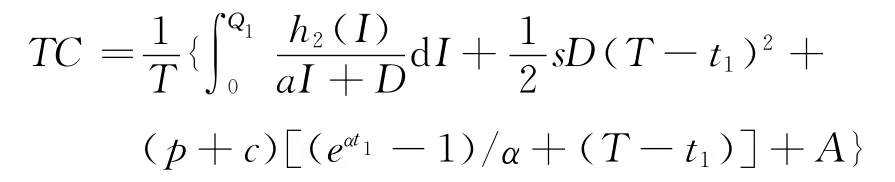
类似于模型1，要确定两个决策变量t1，T的最优值，使得系统的平均费用TC最小。同理t1，T的最优值必满足下列方程组：

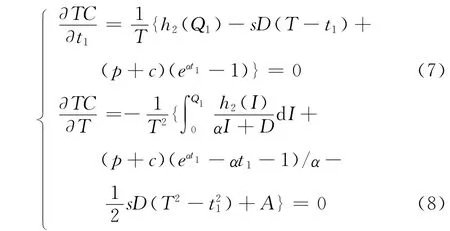
同理可得下面的结论。

定理3 上述非线性方程组（7）、（8）存在唯一的一组解。

证明令（8）等式的左边为

而

定理4 上述方程组的唯一的一组解（T＊，t＊1）使得平均费用函数TC达到最小值。

证明由于

以及

而

所以

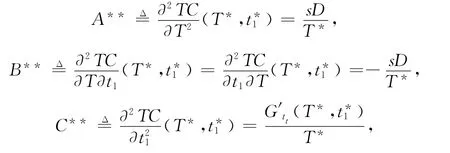
则

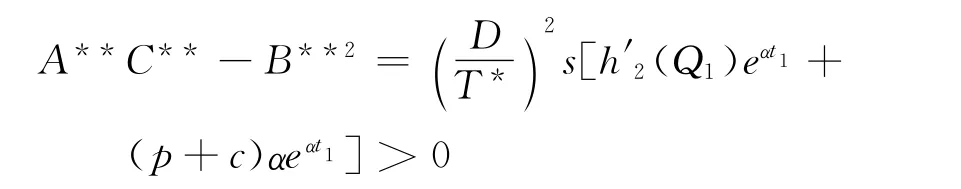
所以TC在（T＊，t＊1）处的海森矩阵正定。故（T＊，t＊1）是TC的整体唯一的最小值点。

4 特例

5 结束语

在假设经典的经济批量模型中允许短缺，但短缺量完全延期供给的变质物品库存的基础上，假定了在订货费用是可变的前提下，建立了2个模型。模型1是库存费和短缺费均是关于时间的变化函数，模型2库存费是关于库存量的变化函数。并且对2个模型决策变量的解的存在性与唯一性给予证明，从不同角度研究了这些变量对库存系统的最优决策的影响，更全面而真实地揭示了这类物品的存储规律，从而具有一定的实际意义。

［1］Weiss H.Economic order quantity models with nonlinear holding costs ［J］.European Journal of Operational Research，1982，9（1）：56-60.

［2］M.Goh.EOQ Models with General Demand and Holding Cost Functions［J］.European Journal of Operational Research，1994，73（1）：50-54.

［3］毛晓丽.变库存费的变质性物品的EOQ模型［J］.武汉科技大学学报（自然科学版），2001，24（3）：322-324.

［4］毛晓丽.变库存费的变质性物品的最优订货策略［J］.经济数学，2001，18（3）：70-74.

［5］Mark Ferguson，Vaidy Jayaraman，Gilvan C Souza.Note：An application of the EOQ model with nonlinear holding cost to inventory management of perishables［J］.European Journal of Operational Research，2007，180（2）：485-490.

［6］Lakdere Benkherouf.On a stochastic inventory model with ageneralized holding costs［J］.European Journal of Operational Research，2007，182（2）：730-737.