结冰分裂导线舞动振幅分析✳
2012-12-03樊社新莫以为朱江新
樊社新,莫以为,朱江新
(1.广西制造系统与先进制造技术重点实验室,广西南宁 530004;2.广西大学机械学院,广西南宁 530004)
引 言
超高压输电线路的结构为分裂导线。结冰分裂导线比结冰单导线更容易发生舞动[1]。超高压输电线路是电网的主干,它的输电安全关系着国民经济的发展。因此就电网的输电安全而言,研究结冰分裂导线舞动比研究结冰单导线舞动更为重要。
中国的东北地区、华北地区及华中地区多次发生结冰分裂导线舞动,导致相线相碰,使输电中断,甚至子导线断裂和杆塔的严重破坏[2~4]。
国内外的学者在努力地揭示冰分裂导线的舞动机理[5~15]。尽管研究角度、方法不同,但基本可归结为从负阻尼或负刚度产生动力失稳的角度阐述结冰分裂导线舞动机理。
从工程的角度来看,若结冰分裂导线振动幅值小于相线相碰值,可视为不舞动,因为振动幅值小于相线相碰值时,不导致输电中断,即使位移大,也是大位移、小变形的振动,不会导致导线断裂和杆塔的破坏。因此研究结冰分裂导线振动达到一定幅值后的振幅的变化规律有重要的工程意义。本文将从功能的角度研究这一问题。
1 能量关系
1.1 基本假设
根据作者对 1989年湖北汉江中山口 500 kV大跨越舞动的实地观察以及文献 [16]报道的实地观察知:结冰分裂导线的轴线(以下简称轴线)的运动、分裂圆半径绕轴线的转动(即子导线相对轴线的转动)服从变幅同频的正弦或余弦规律;轴线上的点的运动轨迹为椭圆,分裂圆半径绕轴线转动的幅值与轴线运动的幅值几乎同步增长。据此,提出假设如下:轴线的运动、分裂圆半径绕轴线的转动服从变幅同频的正弦或余弦规律;轴线上的点的运动轨迹为椭圆;分裂圆半径的绕轴线转角的幅值与轴线的运动成比例。
从上述假设可得到半波舞动位移表达式
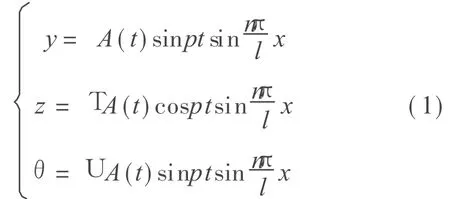
式中 y,z,θ分别为轴线在铅垂方向的位移、水平方向的位移、分裂圆半径的绕轴线的转角;t为时间;T和U为比例系数;p为角频率;n为正整数;l为档长;x轴为档端连线,假定x轴水平。
1.2 功能表达式
本节给出结冰分裂导线的动能、扭转变形能及气动力的功的表达式。
根据 Parkinson的理论[17],舞动达到较大的幅值至少需要1 000个周期。因此设:A′(t)≪p A(t),由式(1)与上述不等式可得
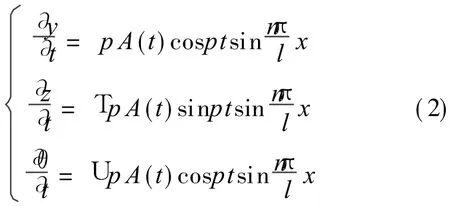
1.2.1 动能、扭转变形能与重力势能
子导线半径远小于分裂圆的半径,因此不计子导线绕自身轴线转动的动能。作用在子导线上的气动扭矩远小于气动力对分裂导线轴线的扭矩,因此不计子导线绕自身轴线扭转的变形能。视间隔棒为刚体。
结冰分裂导线的动能E的表达式为
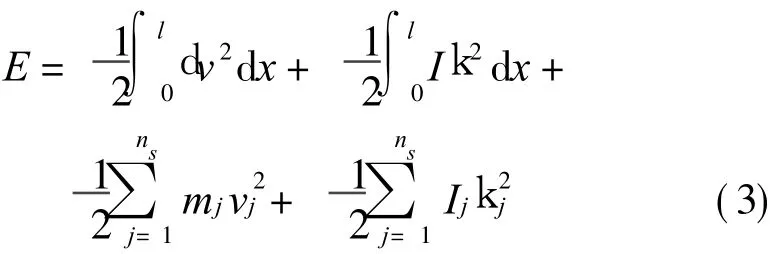
以 T表示周期,经历一个周期动能增量ΔE的表达式为

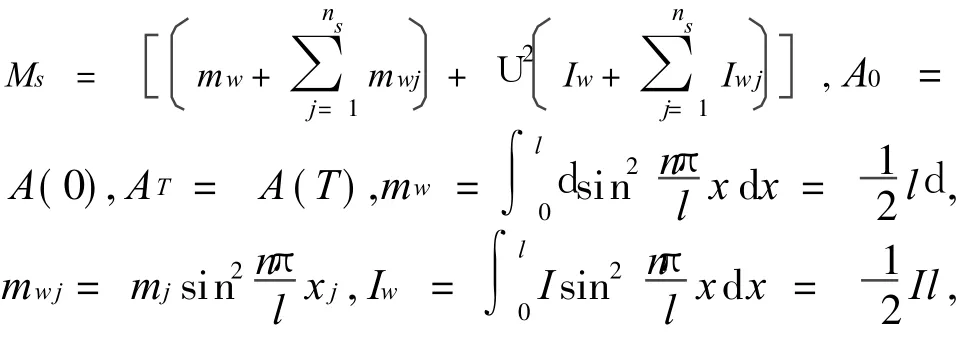
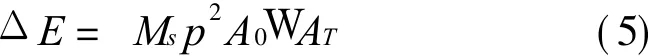
式中 Kn为结冰分裂导线的扭转刚度。由此可得经历一个周期扭转变形能的增量ΔU=0。
因为,W AT(T)≪A0,经历一个周期的重力势能增量亦可不计。
1.2.2 经历一个周期气动力的功的表达式
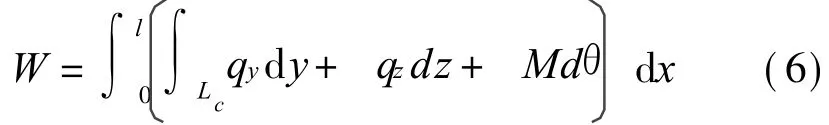
气动力的功的表达式为式中 Lc为一个周期上的轨迹,qy为升力,qz为阻力,M为力矩。设它们的表达式为:式中 y′表示 y对时间的导数,余类推。
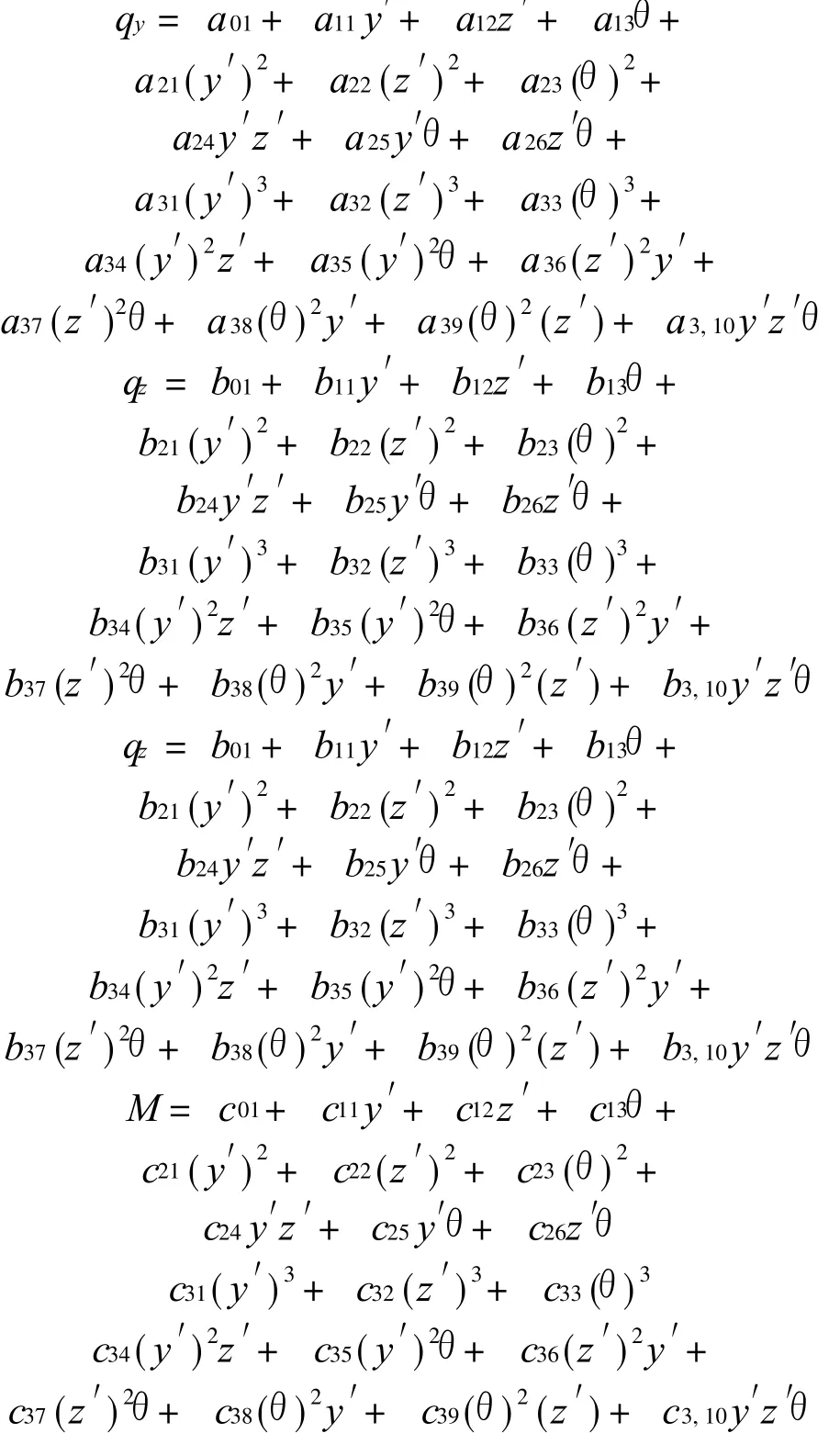
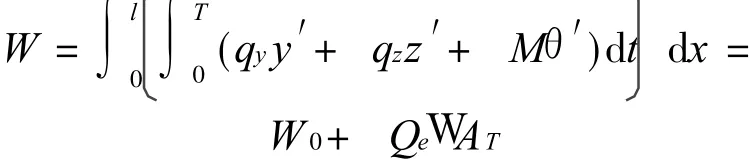
2 舞动振幅增量与碰线分析
子导线结冰后,各层绞线被冰裹紧,因此,不计子导线的内阻尼,由功能关系有
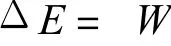
即
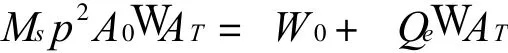
显然,由此可推出:W AT> 0的充要条件是:W 0+QeW AT> 0;W AT=0的充要条件是:W0+QeW AT=0;W AT<0的充要条件是:W0+Qe W AT<0。
2.1.1 关于W AT> 0的分析
显然,由振幅增量的表达式为
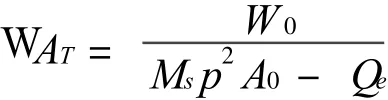
若W 0> 0,Ms p2A0-Qe> 0,即Qe < Ms p2A0,W AT随着W 0与Qe单调增加。
若 W0< 0,Ms p2A0-Qe< 0,因为 Ms p2A0> 0恒成立 ,从而Qe> 0,W AT随W 0单调减小 ,从而W 0的绝对值愈大,W AT愈大;W AT随Qe单调减小即Qe愈接近Ms p2A0,W AT愈大。
2.1.2 关于W AT<0的分析
W0> 0,Ms p2A0-Qe< 0。 W AT随 W 0单调增加 ,即W 0愈大,W AT的绝对值愈大;W AT随 Qe单调减小,从而 Qe愈接近Msp2A0,W AT绝对值的愈大。
W0<0,Ms p2A0-Qe> 0,W AT随着 W 0单调增加,即W 0的绝对值愈大,W AT的绝对值愈大;W AT随Qe单调减小,Qe愈接近Ms p2A0,W AT绝对值的愈大。
2.1.3 关于W AT==0的分析
W AT=0⇔ W 0=0⇒ Qe W AT=0⇒ W 0+Qe W AT=0,即气动力的功为零。
2.1.4 碰线分析
以Rc表示碰线值(此值由布线方式决定),发生舞动的条件可表为

若所有的WAT> 0,则输电线处于动力失稳状态,即
舞动,将导致碰线,甚至导致输电线断裂及杆塔破坏。
若 m个WAT≤ 0,k个WAT> 0,(m+k=n),且R,则输电线处于动力失稳与稳2.1.5 气动力对舞动振幅增量的影响
从附录中ak(i1),b(k1i
表1为给定初始振幅A0后,气动力在10个周期上的功的构成比例表。计算数据与后文第三节中的数据相同。
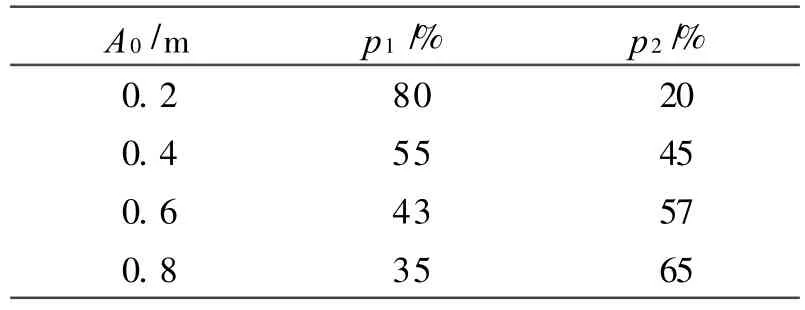
表1 气动力的功的构成比例表Tab.1 The composing proportion table of the work of aerodynam ic forces
表中,A0为初始振幅,p1为气动力中的常数项与线性项的功在气动力总功中的百分比,p2为气动力中的二次项与三次项的功在气动力总功中的百分比。
3 算 例
以湖北汉江中山口大跨越舞动为例。参数如下:l=1 055 m,d=10.33 kg/m,mj=14 kg,R=0.46 m,T=0.7,U=0.16m-1,ns=15,nc=3,n=3,T=3.00 s,A0=0.20m。
以下气动力系数曲线取自参考文献 [18]。
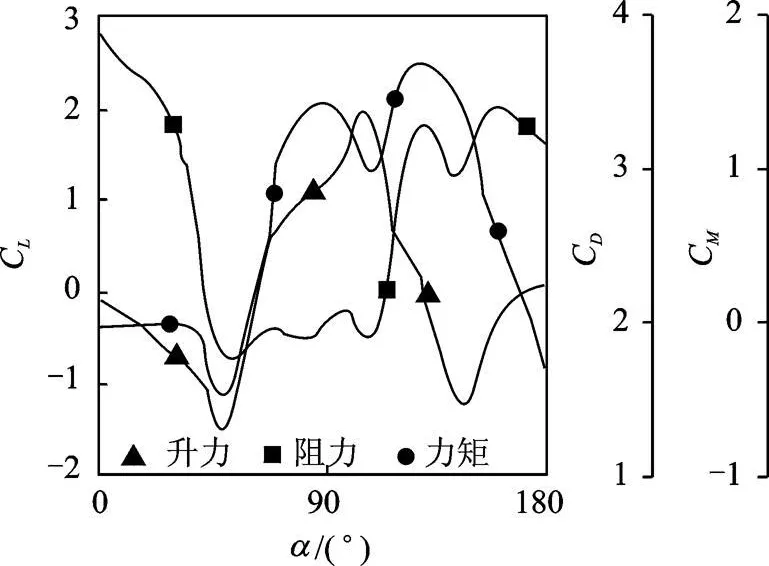
图1 气动力系数曲线Fig.1 The curve of aerodynamic forces
图1中的CL,CD,CM,T分别为升力系数、阻力系数、力矩系数与攻角。
取风速为中山口大跨越第4次舞动时的实际风速的均值10m/s,空气密度为1.293 kg/m3。舞动峰峰值为2m,即舞动幅值为 1m。
拟合出气动力系数曲线表达式,将此表达式与风速及空气密度代入气动力的表达式,再将气动力的表达式按泰勒公式展开,即可得到qy,qz,M的表达式中的各系数。
为了说明气动力中的各项对振幅增量的影响,按3种情况分别计算振幅的增长。这3种情况是:线性气动力即气动力只含常数项与线性项;二阶非线性气动力即气动力含常数项与线性项及二次非线性项;三阶非线性气动力即气动力含常数项与线性项、二次与三次非线性项。振幅从初值至稳态的计算结果如图2~4。
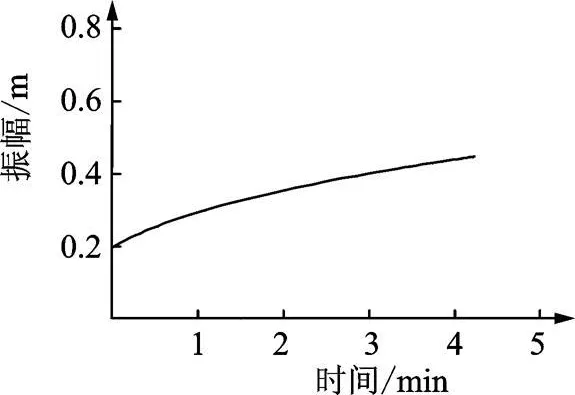
图2 线性气动力对应的振幅曲线Fig.2 Theamplitude curve corresponding with linear item in aerodynam ic forces
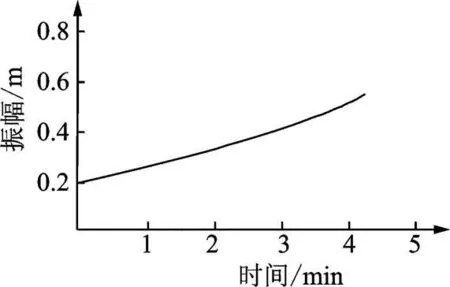
图3 二阶非线性气动力对应的振幅曲线Fig.3 The amplitude curve corresponding with two order item in aerodynamic forces
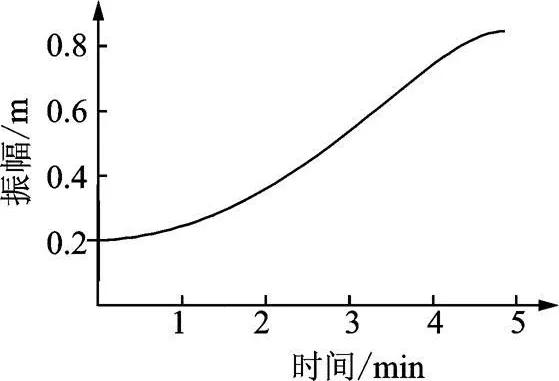
图4 三阶非线性气动力对应的振幅曲线Fig.4 The amplitude curve corresponding with three order item in aerodynamic forces
计算结果与观察结果 [19]有一定的误差,计算结果中舞动幅值达到约 0.85 m时,进入稳态,与观察结果有15%的误差。误差的主要原因是气动力与实际情况有差异,因为气动力是通过风洞实验得到的,风洞中的气流与实际情况难以一致。
4 结 论
当舞动的振幅较小时,气动力中常数项与线性项的功是气动力总功中的主要部分;当舞动的振幅为中等时,气动力中常数项与线性项的功与非线性项的功在气动力总功中的比例相近;当舞动的振幅为较大时,气动力中非线性项的功在气动力总功中的比例大于常数项与线性项的功在气动力总功中的比例。
[1] Leppers.Spacers removed to combat galloping[J].Electrical World,1977,187(9):70—72.
[2] 张宏志.大面积导线覆冰舞动事故的调查与分析 [J].东北电力技术,2001,22(2):15—19,43.Zhang Hong-zhi.Investigation and analysis on the accidents of large-area line conductors ice coating and ga lloping[J].Northeast Electric Pow er Techno logy,2001,22(2):15—19,43.
[3] 胡毅.输电线路大范围冰害事故分析及对策[J].高电压技术,2005,31(3):14—15.Hu Yi.Analysis and countermeasures for large area accident cause by icing on transmission line[J].High Voltage Engineering,2005,31(3):14—15.
[4] 黄经亚.架空送电线路导线舞动的分析研究[J].中国电力 ,1995,28(2):21—26.Huang Jing-ya.Analysis of overhead transm-ission line ga lloping[J].Electric Pow er in China,1995,28(2):21—26.
[5] 陈晓明,邓洪洲,王肇民.大跨越输电线路舞动稳定性研究 [J].工程力学,2004,21(1):56—60.Chen Xiao-ming,Deng Hong-zhou,Wang Zhao-m in.Conductor galloping stability ana lysis of long span transm ission system [J].Engineering M echanics,2004,21(1):56—60.
[6] Braun A L,Aw ruch A M.Aerodynam ic and aeroelastic analysis of bund led cables by numerical simulation[J].Journal of Sound and Vibration,2005,284(12):51—73.
[7] Zhang Q,Popp lew ell N,Shah A H.Galloping of bundle conductor[J].Journal of Sound and V ibration,2000,234(1):115—134.
[8] Y Nakam ura.Ga lloping of bundied power line conductors[J].J.of Sound and Vibration,1980,73(3):363—377.
[9] Simpson A.Determ ination of the natural frequencies of multiconduc tor overhead transm ission line[J].Journal of Sound and Vibration,1972,20(4):417—449.
[10]Den Hartog JP.Transm ission line vibration due to sleet[J].AIEE Trans,1932,51(91):1 074—1 086.
[11]N igo l O,Buchan P G.Conductor ga lloping,partΙΙ-torsional mechanism [J].IEEE Trans.on PAS,1981,100(2):708—723.
[12]樊社新 ,何国金,廖小平 ,等.结冰导线舞动机制分析[J].中国电机工程学报,2006,26(14):131—133.Fan Shexin,He Guo jin,Liao Xiaoping,et al.Ana lysis of gallopingm echanism of iced conductor[J].Proceeding of the CSEE,2006,26(14):131—133.
[13]何锃,赵高煜.分裂导线扭转舞动分析的动力学建模[J].工程力学,2001,18(2):126—134.He Zeng,Zhao Gao-yu.On galloping of bundled conduc tors in overhead transmission with large torsional motion[J].Engineering Mechaics,2001,18(2):126—134.
[14]樊社新 ,何国金,廖小平,等.结冰分裂导线舞动建模研究 [J].中国电机工程学报,2005,25(25):340—343.Fan Shexin,He Guojin,Liao Xiaoping,et al.The galloping model of iced bundled conductors[J].Proceeding of the CSEE,2005,25(25):340—343.
[15]Ahmad Jamaleddine,Louis Cloutier.A non-linear finite-elementmodel to calculate the twistmoment of a four-conductor bund le[J].Electric Power Systems Research,1988,14(3):191—205.
[16]Havard D G,Poh lman JC.Field trials of detuning pendulums for controlling galloping of singleand bundle conductors[J].IEEE Transac tions on Power Apparatus,1984,103(2):318—327.
[17]Parkinson G.Phenomena and modeling of flow-induced vibrations of bluff bodies[J].Prog.Aero-Space Sci.,1989,(26):169—224.
[18]何锃,李国兴.中山口大跨越导线舞动的分析计算 [J].高电压技术,1997,23(4):12—14.He Zeng,Li Guoxin.Analysis galloping of Zhongshankou Large Span Overhead Line[J].High Vo ltage Engineering,1997,23(4):12—14.
[19]李国兴,杨肇成,李奠川,等.中山口大跨越舞动的防治与研究 [J].中国电力,1995,(5):56—61.Li Guoxin,Yang Zhaocheng,Li Dianchuan,et al.Studying and contro ling on galloping of Zhongshankou large span overhead line[J].Electric Pow er in China,1995,(5):56—61.
