面内弹性绳系卫星系统的内共振✳

夏 洁,庞兆君,金栋平

(南京航空航天大学振动工程研究所,机械强度与振动国家重点实验室 ,江苏 南京 210016)

引 言

绳系卫星作为一种新型空间技术具有巨大潜力,正日益受到学术和航天界的关注[1～5]。绳系卫星系统为高维非线性动力学系统,由于绳系卫星在工作状态往往需要稳定的状态保持,因此研究状态保持阶段绳系卫星的非线性行为具有重要意义。Nixon对于绳系卫星面内外动力学行为进行了解析和数值研究,给出了系统参数对于周期、概周期及混沌运动的影响[6]。 Fujii等研究了系绳弹性和轨道偏心率引起的绳系卫星状态保持阶段的分叉问题[7]。Misra等研究了状态保持阶段的面内非线性动力学[8]。此后,他们又考虑了面内外耦合的三维绳系卫星系统,结果表明圆轨道和椭圆轨道均存在混沌运动且混沌区随Hamilton函数的增加而增大。Celletti和 Sidorenko等研究了“哑铃”型绳系卫星系统在圆轨道及椭圆轨道上的姿态动力学。研究表明,圆轨道绳系卫星系统的局部平衡位置是稳定的,而椭圆轨道的平衡位置呈现出周期时变性[9]。此后,他们还研究了不计系绳质量时弹性连接的绳系卫星系统面内周期运动的分叉及其稳定性问题[10]。

当考虑系绳弹性时,由于系绳纵向和面内俯仰运动耦合,使得绳系卫星系统成为一复杂的含陀螺项的非线性动力学系统。在现有的研究中,人们大多集中于周期、概周期、混沌及其运动稳定性分析,而对绳系卫星系统运动耦合导致的非线性共振尚未有深入研究。本文针对一弹性绳系卫星系统的非线性耦合振动问题,应用多尺度方法研究了其在状态保持阶段的非线性共振,分析了可能的参数组合所导致的共振问题,获得了基于 Jacobi椭圆函数的绳系卫星系统 2∶1内共振的解析解。

1 系统模型

研究“弹簧-质点”型面内绳系卫星系统。点质量分别为m1和m2的卫星通过质量为mt的一均质分布的弹簧相连,系统质心O1沿偏心率为e的未扰 Kepler椭圆轨道运动,考虑整个系统在轨道面内运动,如图1所示。设弹簧仅发生沿其自身的纵向振动,只考虑重力梯度且重力场局部呈线性。建立固连于地心的惯性坐标系O-XY和固连于系统质心的轨道坐标系O1-xy。轨道坐标系单位矢量i和 j分别指向天顶和绳系卫星系统的质心飞行方向。

根据图1可知,系统质心和卫星的位矢分别为

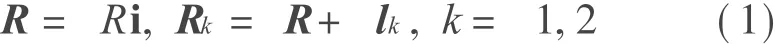
式中 l k=(-1)klk(i cosθ+ j sinθ)为卫星相对系统质心的位矢,其中lk=l[1-(mk+ 0.5mt)/m],m=m1+m2+mt为系统总质量。弹簧长度l=l0(1+X),l0为未变形的弹簧原长,X为弹簧的线弹性应变。系统的广义主动力Qr和惯性力Q*r为

式中 _e=3.986×1014m3/s2为地球重力常数。Tk=k(l-l0)lk/lk为弹簧张力,k为弹性系数。vkr为卫星关于广义坐标的伪速度。根据 Kane方程Qr+Q*r=0,可得状态保持阶段系统动力学方程

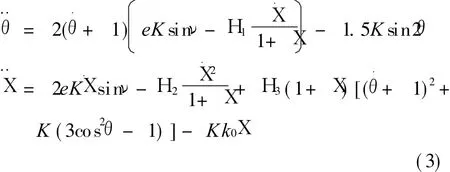
式中 “.”表示对真近点角ν的导数,K=(1+e cosν)-1,无量纲弹性系数 k0=ka3(1-e2)3/(m^_e),m^=m1(m2+mt)/m,a为椭圆轨道半长轴。其中式中~m=(m1+0.5mt)(m2+0.5mt)/m-mt/6。方程(3)为绳系卫星系统俯仰运动和系绳弹性变形相互耦合的自治非线性动力学系统,可能存在非线性共振现象。

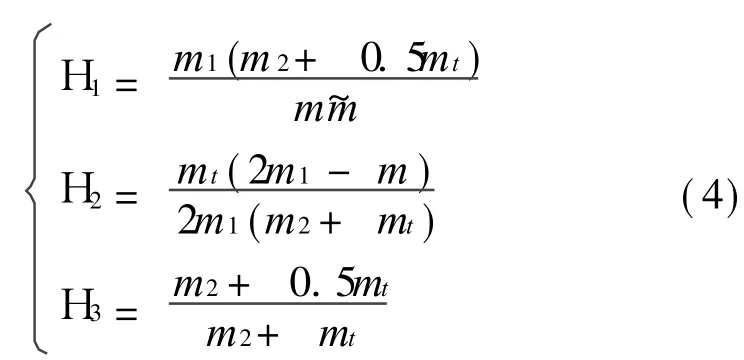
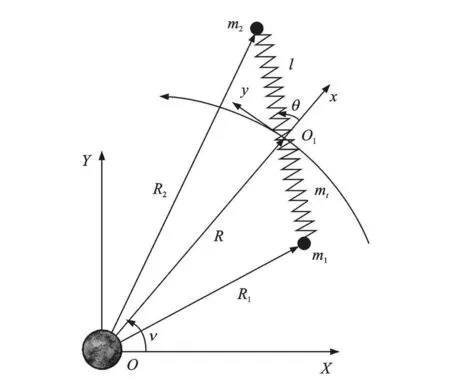
图1 面内绳系卫星简化模型Fig.1 A simp lifiedmodel for in-plane tethered satellite

2 共振条件分析

轨道偏心率的作用是在动力学方程中引入了一参数激励。考虑小轨道偏心率情形以致可令e=T e,这里T为一小量。此时方程(3)的派生系统成为

式中 c1=2H 1,c2=2H 3,k11=3,k22=k0-3H3。k 1,2为派生系统的固有频率,满足特征方程k4-(k11+

k22+c1 c2)k2+k11 k22=0,k 2＞ k 1。

考虑一次近似解的情况,系统固有频率k1,2和激励频率k=1可能出现 2∶1内共振、2次超谐共振、1/2次亚谐共振以及参激组合共振的情况。选取两组典型参数分析上述共振发生的可能性。取弹簧线密度 0.04 kg/m,长度 l=5 km,卫星质量m1=m2=100 kg。系统固有频率k 1,2及其组合k2±k1随参数k的变化如图2(a),(b)所示。可见,k2±k 1始终远离激励频率k=1。当时,k1≈2k,系统发生 1/2次亚谐共振,此时k2=2.110。取弹簧弹性系数,系统固有频率k1,2及其组合k2±k1随参数l的变化如图2(c),(d)所示。k1始终在附近,k2远大于固有频率k1和激励频率k。可见,系统可能会发生2∶1内共振和 1/2次亚谐共振,但轨道偏心率所引起的亚谐共振并不会与系统内共振同时发生。

图2 椭圆轨道共振分析Fig.2 Resonance analysis for ellipticalorbit

3 内共振分析

考虑到计入轨道偏心率后并不会影响系统的内共振,下面具体分析圆轨道内共振情形。此时系统动力学方程简化为

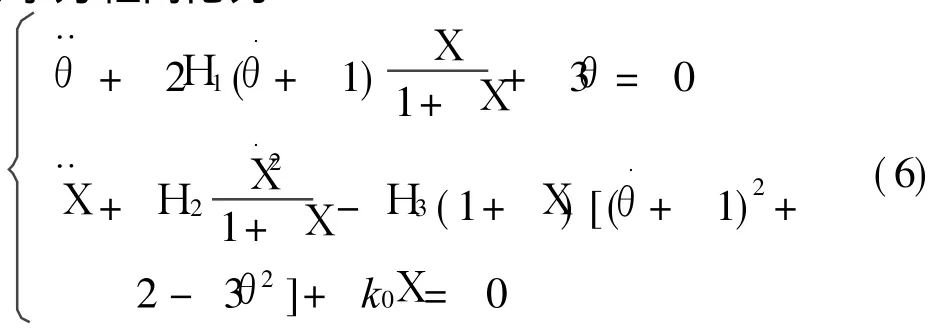
为消除常数项 ,可令a=X-2H3/H4,H4=k0-2H3。应用多尺度法求解系统(6)的一次近似解[11]。设

式中 T0=ν,T1=Tν。 将式(7)代入方程 (6)并比较方程两边T的同次幂系数得到

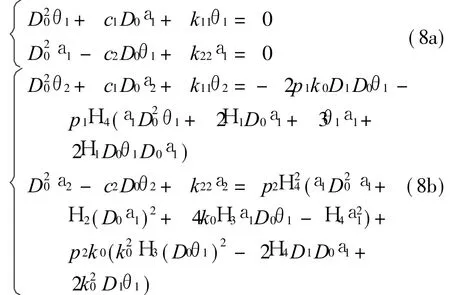
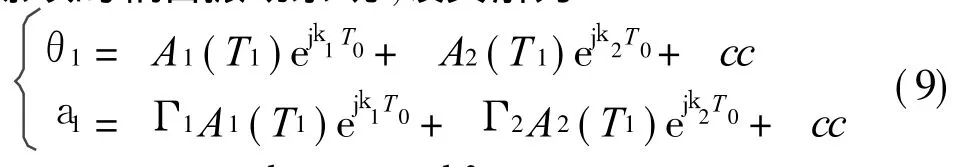
式中 Dr= ∂/∂Tr,r= 0,1。 p1=1/k0,p2=p1/H4,c1=2H 1H4/k0,c2=2k0H 3/H4。方程(8a)为一含有陀螺项的耦合振动系统,设其解为式中 Γr=j c2k r/(k22-k r2),r=1,2,cc代表前面各项的共轭,k 1,2为系统的固有频率。将式(9)代入方程(8b)发现满足k2=2k1+Te,e=O(1)时系统发生内共振。设方程(8b)的一个特解形如

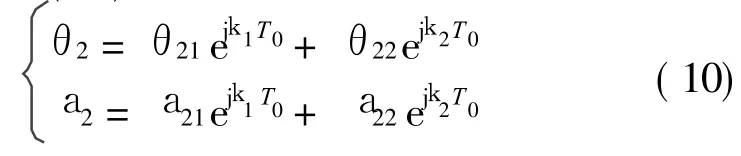
根据可解性条件,有

式中

其中

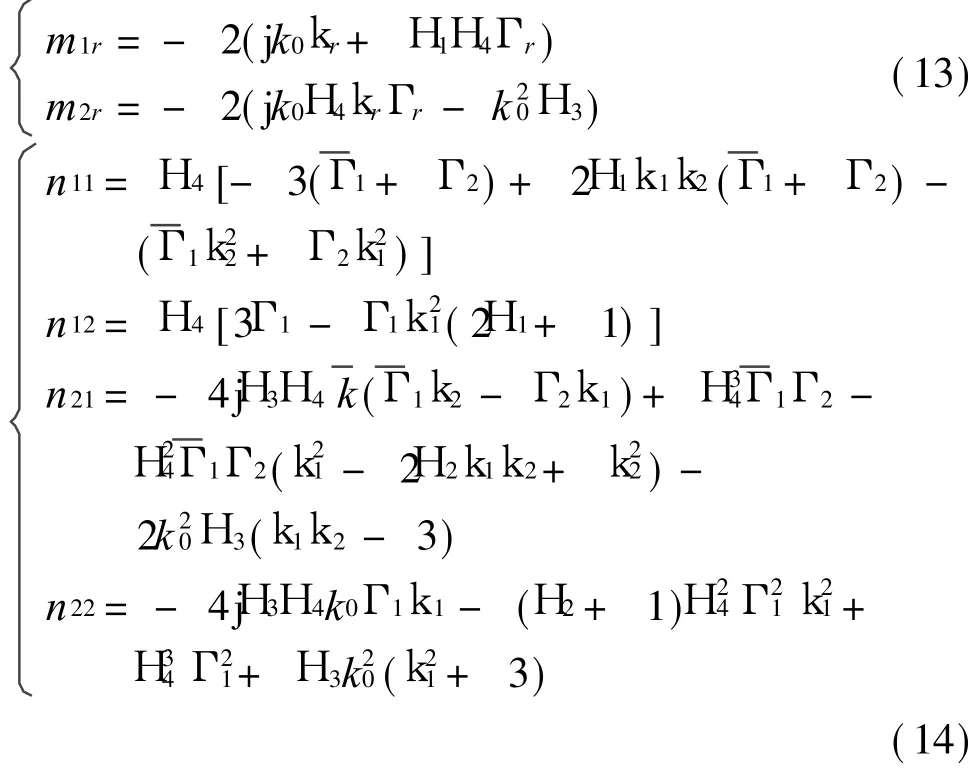
整理后获得消除永年项的条件为

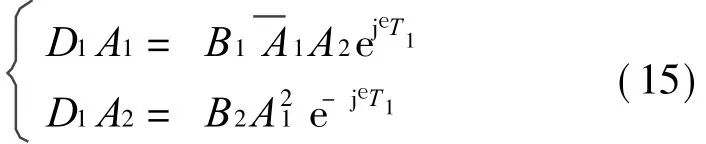
式中 Br= c2 n1r-c1Γr n2r/(c2m1r-c1Γrm 2r)。 令Ar(T1)=ar(T1)ejUr(T1)/2,代入方程(15)后分离实部和虚部,得到一阶近似解振幅和相位满足的微分方程组

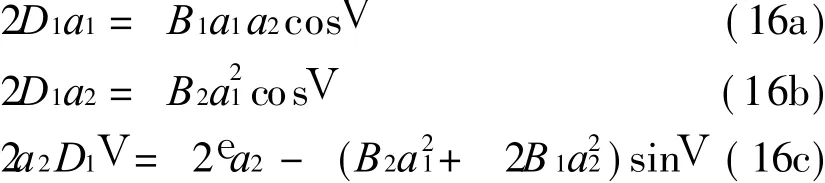
式中 V=U2-2U1+e T1。由方程 (16a)和 (16b)获得全微分关系

式中 λ=-B1/B2。 当λ＞ 0时 ,方程 (17)为 (a1,a2)平面上的椭圆;当λ＜0时,方程(17)为(a1,a2)平面上的双曲线。本例中λ＞ 0。视a2为间接变量,由方程(16b)和 (16c)可得

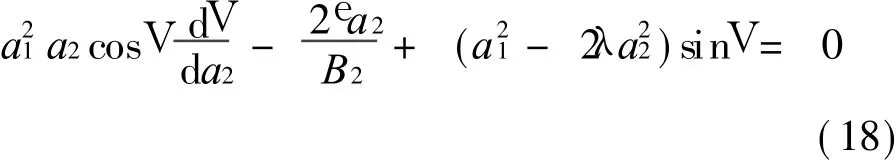
利用全微分关系将方程(18)整理后,有

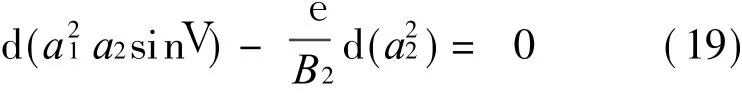
积分可得

a21a2 sin V-Be2a22= L= cons t (20)

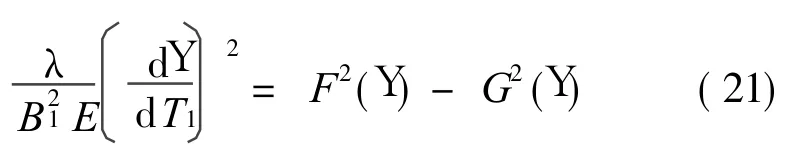
式中的一元函数F(Y)和G(Y)分别定义为

通常,函数 F(Y)与G(Y)有 3个交点。由于Y＞ 0,交点Y2和Y3对应于定常解D1 a1=0,即原系统的周期振动。当Y∈ (Y2,Y3),原系统作非周期振动,如图3所示。引入变换Y3-Y=(Y3-Y2)sin2y,式(21)即可借助

图3 周期和非周期振动条件Fig.3 The conditions for periodic and non-periodic oscillations

Jacobi椭圆函数进行积分,从而给出

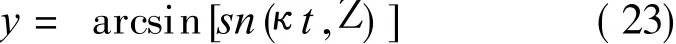
作为特例,当函数G(Y)与F(Y)的一支相切时(Y2=Y3),则

此时原系统对应周期振动。然而,任意小扰动都会导致函数 F(Y)与 G(Y)有3个交点,使其成为非周期振动。

4 算例研究

首先分析实现完全内共振的条件,即e=0。取无量纲参数H1=0.735,H 2=-1.326和 H3=0.526。当弹性系数 k=0.000 234 N/m或 k=0.000 408 N/m时,系统满足 2∶1完全内共振条件,如图4所示。

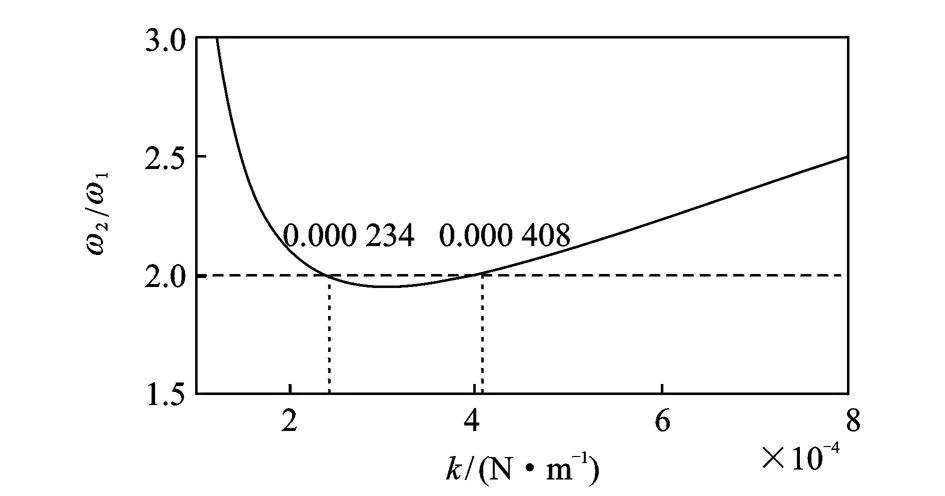
图4 完全内共振条件Fig.4 The conditions for fully resonance

现取 k=0.000 5N/m,获得k1=1.541和k2=3.230,即任一非完全内共振的情况进行数值研究。设振幅和相位初值为a10=0.04,T20=0.02和U10=U20=0.01。使用方程(16)和解析解(24)计算a1和a2的时间历程,结果如图5所示。结果显示在ν=12 rad时,a1和a2分别达到最大值:a1的解析结果为 0.050 1,数值结果为 0.050 8;a2的解析结果为0.017 4,数值结果为0.017 2。在整个时间历程内,a1的解析结果与数值结果的误差绝对值始终小于 0.001,a2的误差绝对值则始终在0.000 5以内。解析结果和数值结果吻合较好。从图5可见,两种模态表现为异步振动,能量发生相互转换:一个模态的能量减小时,另一个模态的能量增大。

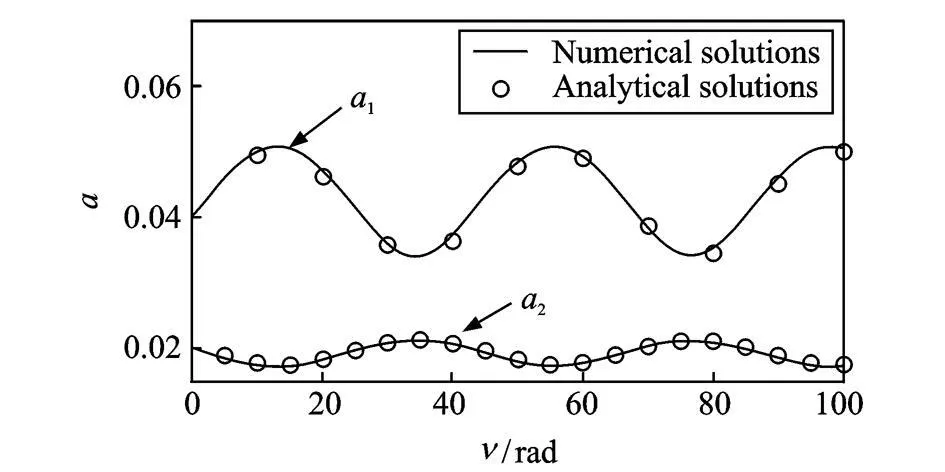
图5 周期振动响应Fig.5 Periodic oscillation responses versusν

取参数W=k2-2k1,图6给出了振幅最大值随参数W的变化关系。由图6(a)可知,a1的最大振幅为0.65,发 生在 W= 0.01,此 时弹性 系数 k=0.000 419 N/m。 从图6(b)可见,当W∈ (-0.028,0.038),即k∈ (0.000 384,0.000 434)N/m时 ,a2的振幅出现了饱和现象,始终保持在初值 0.02上。在参数W接近零时,解析解和数值解吻合最好。

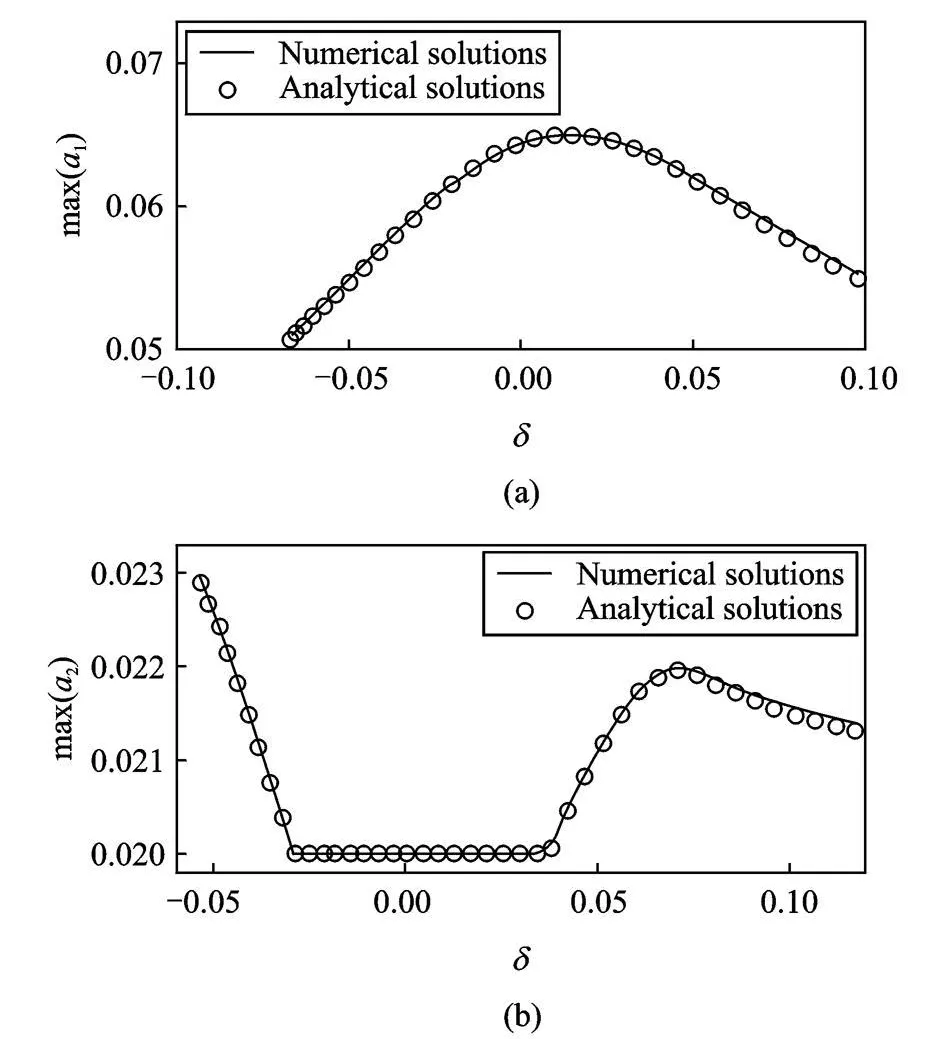
图6 参数W对周期振动最大幅值的影响Fig.6 The effect of parameter W on maximum of periodic oscillation

非线性振动周期依赖于振幅。给定a20=0.01,研究a10对振动周期的影响,图7(a)给出了a10变化时数值积分得到的模态振幅运动的周期T与解析表达式计算得到的周期的对比。可以看出二者吻合较好。注意到a10=0.04时,解析解得到的周期 T=40.8 rad和数值积分得到的周期T=39.7 rad均与图6给出的算例一致。图7(b)给出了根据解析表达式得到的周期随初始振幅的变化情况。从图7(b)可见,模态振幅运动的周期随a10的增大而减小,随a20的增大而增大。

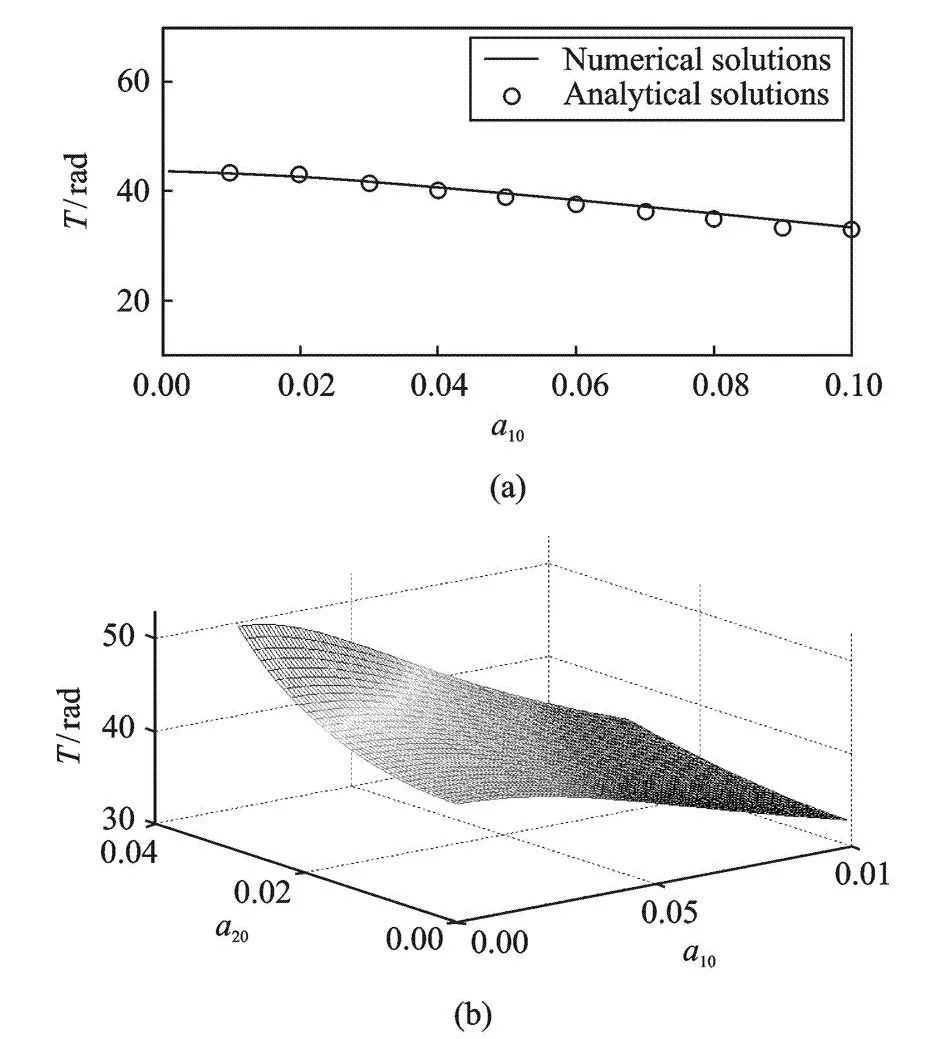
图7 初始模态幅值对周期的影响Fig.7 The effect of initia lmode amp litudes on the period

5 结 论

考虑弹性的绳系卫星系统可发生非线性 2∶1内共振,其模态幅值可借助Jacobi椭圆函数表示。结果表明,系统的周期运动只是临界稳定,任何微小的扰动都会使其成为非周期运动。在非线性共振时,模态振幅的周期与其初值有关,振动能量在两个模态幅值间相互传递。在一个小的调谐参数范围上,有一个模态振幅会出现饱和现象。

[1] Cosmo M L,Lorenzini E C.Tethers in Space Handbook(3rd ed.)[M].W ashington DC,NASA,1997.

[2] Modi V J,Lakshmanan P K,M isra A K.Dynam ics and contro l of tethered spacecraft:a brief overview[A].A IAA Dynam ics Specialist Conference[C].Long Beach,California,United States,1990.

[3] Kumar K D.Review of dynam ics and control of nonelectrodynam ic tethered satellite systems[J].Journal of Spacecraftand Rockets,2006,43(4):705—720.

[4] Cartmell M P,M ckenzie D J.A review of space tether research[J]. Progress in Aerospace Sciences,2008,44(1):1—21.

[5] W en H,Jin D P,Hu H Y.Advances in dynam ics and control of tethered satellite systems[J].Ac ta Mechanica Sinica,2008,24(3):229—241.

[6] Nixon M S.Nonlinear dynam ics and chaos of tethered satellite system[D].PhD Thesis,Department of Mechanical Engineering M cGill University,Montreal,1996.

[7] Fujii H A,IchikiW.Nonlinear dynamics of the tethered subsatellite system in the station keeping phase[J].Journal of Guidance,Contro l,and Dynamics,1997,20(2):403—406.

[8] M isra A K,Nixon M S,ModiV J.Nonlinear dynamics of two-body tethered satellite system s: Constant length case[J].Journal of the Astronautical Sciences,2001,49(2):219—236.

[9] Celletti A,Sidorenko V V.Some properties of the dumbbell satelliteattitude dynam ics[J].Celestial Mechanics and Dynamical Astronomy,2008,101(1-2):105—126.[10]Sidorenko V V,Celletti A A.“ Spring-mass” modelof

tethered satellite system s:p roperties of p lanar periodic motions[J].CelestialMechanics and Dynam ical A stronomy,2010,107(1-2):209—231.

[11]Nayfeh A H,Mook D T.Non linear Oscillations[M].New York:W iley InterScience,1979.