磁性液体阻尼减振器动力学建模及实验✳
2012-12-03杨文明李德才冯振华
杨文明,李德才,冯振华
(北京交通大学机械与电子控制工程学院,北京 100044)
引 言
磁性液体是一种由包覆有表面活性剂的纳米铁磁性或亚铁磁性颗粒分散于液态载液中形成的稳定的胶态悬浮液。在磁性液体应用于实际之初,人们就提出了将磁性液体应用于阻尼的设想[1],后来,K.Raj和 R.M oskow itz于 1980年综述了磁性液体阻尼技术的诸多应用[2]。之后,应用磁性液体的阻尼器被发展为多种类型。1987年,Katsuto Nakatsuka等人提出了一种活塞式磁性液体阻尼器[3],并将这种阻尼器与空气弹簧组合用来控制载物台的振动,Toyohisa Fujita等人将电流变液与磁性液体混合代替活塞式阻尼器中的磁性液体[4,5],发现改进后的阻尼器可阻尼更宽频率范围的振动。 Hideaki Fukuda等人则在活塞式磁性液体阻尼器的外部安装电磁铁来达到对振动进行主动控制的目的[6,7]。1998年,AbéM asato等人提出了调谐磁性液体阻尼器[8],后来由Yasuhiro Ohira等人建立了这种阻尼器的分析模型[9,10],并经仿真和实验验证了它的有效性。2002年,V.G.Bashtovoi提出了一种磁性液体动力吸振器[10],发现它最适用于阻尼小振幅(小于 1 mm)和小频率(小于1 Hz)的振动。最近几年,人们为了减小阻尼过程中的生热,提出了磁性液体胶体阻尼器[12],为了将阻尼器应用于微型机械,研究了多孔弹性片状磁性液体阻尼器等类型[13]。到现在,有的磁性液体阻尼器已经应用于机械、仪器仪表和航天等领域中,有的则还处于理论分析阶段,但在阻尼器件中作为支撑和阻尼液仍然是磁性液体最具潜力的应用之一。
本文针对要求结构紧凑和能量耗散较小的场合,提出另外一种磁性液体阻尼减振器,建立这种减振器的动力学模型,并实验验证模型的有效性。
1 磁性液体阻尼减振器工作原理
如图1所示,磁性液体阻尼减振器由圆柱形非磁性外壳,充满在外壳内的磁性液体以及浸没在磁性液体中的圆柱形永磁体组成。如果忽略永磁体的重力,根据磁性液体的第二类悬浮原理[14],永磁体将远离外壳内壁,悬浮在磁性液体中央。使用时将外壳与被减振的物体固定,外界的振动将引起永磁体与外壳间的相对运动,从而在磁性液体内部产生具有速度梯度的流动,这样就可以依靠液体的粘性耗能原理耗散能量。
本文中为了研究简便,用一端固定,另一端自由的弹性悬臂梁产生自由振动,梁的示意图和建立的坐标系如图2所示。将未变形时梁的轴线,即各截面形心连成的直线取作 y轴,将梁的对称平面内与y轴垂直的方向取作x轴。梁在对称平面内作弯曲振动,不考虑剪切变形和截面绕中性轴转动对弯曲振动的影响,梁的轴线只有横向位移x(y,t),t为时间变量。阻尼器安装于梁的最低端,而且圆柱形阻尼器的轴线沿振动方向。

图1 磁性液体阻尼减振器结构Fig.1 Structure of ferrofluid damper

图2 弹性悬臂梁Fig.2 The elastic brass plate
2 磁性液体阻尼减振器动力学建模
2.1 弹性悬臂梁振动能量的计算

一端固定,另一端自由的弹性悬臂梁自由振动时具有如下的表达式[15]式中 A为初始偏移量,U=1.875/l,l为梁的长度,k为梁自由振动的频率。
由式(1)可知 ,在时间点tn=(n=0,1,2,… )上,梁处于不受力的平衡位置,只有运动能,此时整个梁的运动能为

式中 S为梁的截面积,d为梁材料的密度。将t=tn以及x0(y)的表达式代入式(3),并经积分计算,可得梁的振动能量为

2.2 磁性液体中粘性耗能的计算
由于梁振动时磁性液体内的粘性耗能,梁的振动被抑制,用梁振动的对数衰减率Λ来衡量这种抑制作用的强弱

式中 Ai为第i次振动的振幅,如果记Wi为振幅 Ai时梁的振动能量,则由式(1),(2)和(3)可知Wi正比于Ai2,从而

如果用ΔW表示第i次振动中磁性液体的粘性耗能,则Wi-1=Wi+ΔW,从而对数衰减率可以表示为

下面计算在梁振动的一个周期T内磁性液体的粘性耗能。假设外壳沿轴线方向较其中的永磁体长很多,认为永磁体只在外壳内的中心部分振动,这时可以忽略永磁体在轴线方向上受到的磁性液体施加的回复力。又假设永磁体和外壳间的间隙较永磁体的尺寸小很多,而且由于外壳随被减振件一起振动的频率较小,所以永磁体和外壳间的间隙内磁性液体的流动可以认为是沿轴线方向上的一维准定常流动。
根据减振器结构的轴对称性,将在三维空间内的问题简化为二维平面问题,如图3所示,可以只考虑图中对称轴以上的部分。圆柱形永磁体悬浮于圆柱形外壳内的磁性液体中,设外壳内径为R,永磁体的质量为m,长度为lm,密度为d m,半径为ra,端面面积为 Sm,外圆柱表面积为 Sa,磁性液体的密度为d f,粘度为Z。忽略永磁体的磁场对磁性液体粘度的影响。认为永磁体在磁性液体中沿径向居中,居中时永磁体和外壳间的间隙为ga。
设外壳沿轴线方向相对于初始位置的位移为x,永磁体相对于外壳的位移为xm,磁性液体相对于外壳的位移为xf,速度为vf。由于忽略磁场和重力对磁性液体的影响,所以间隙内磁性液体流动在r方向上的N-S方程可以简化为

图3 磁性液体阻尼减振器的参数Fig.3 Parameters of ferrofluid damper

图4 永磁体和外壳间的间隙内磁性液体的受力Fig.4 Forces exerted on the ferrofluid between the shell and magnet
即磁性液体内的压力不随坐标r变化,当假设磁性液体对永磁体两端面上某一点的压力分别为p1和p2时,这时磁性液体对永磁体两端面上所有点的压力也为p1和p2,而且与永磁体两端面处于同一x位置的磁性液体内部的压力也为p1和p2。
磁性液体可以看作是牛顿流体[16],其内部的剪切应力可以表示为

由于在间隙内磁性液体进行一维的准定常流动,所以vf不随坐标 x变化,由式 (9)知f也不随坐标x变化,所以间隙内处于同一r位置上的磁性液体层受到相同的剪切应力,故将永磁体外圆柱表面上受到磁性液体的剪切应力统一表示为f a。
对圆柱形永磁体在 x方向上应用牛顿第二定律,有

式中 Sm=πr2a,Sa=2πra lm。假设永磁体相对于外壳的加速度与外壳自身的加速度相比可以忽略,即,则式 (10)成为

为了确定式(11)中等号右端各项的值,需要求得外壳和永磁体间间隙内磁性液体在外壳随被减振件一起振动时的流速分布。以该间隙内半径为r,厚度为d r且与永磁体具有相同长度的磁性液体层为研究对象,如图4所示。令层与永磁体外表面间的径向距离为ya,它是一个变量。结合上面的分析,假设磁性液体层内外侧的磁性液体对层的切应力分别为f1和f2,层左右两端的磁性液体对层的压应力分别为 p1和p2。
对磁性液体层应用牛顿第二定律,有
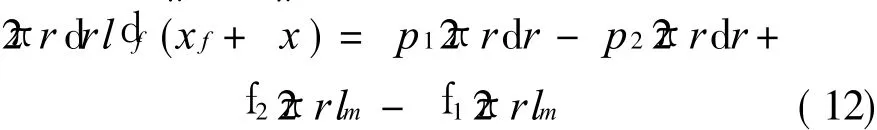
其中液体层外侧的切应力产生的力可用内侧的切应力根据该力沿r方向的变化率求得,即

将式(9)和(13)代入式(12),并认为磁性液体相对于外壳的加速度可以忽略,经化简,有另外,对于外壳和永磁体间隙内磁性液体的流动,有边界条件


求解方程(14),并由边界条件最终可得
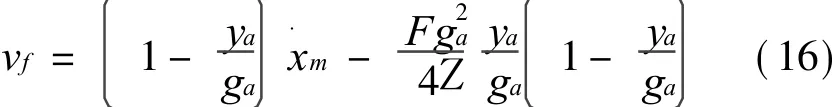
其中

根据式(16),可计算得外壳和永磁体间的间隙内磁性液体的流量为

作用于永磁体圆柱表面上的切应力为
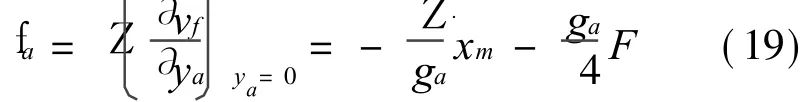
由外壳内所有的磁性液体的质量守恒,可得

将 Sm和式(18)代入式(20),化简得
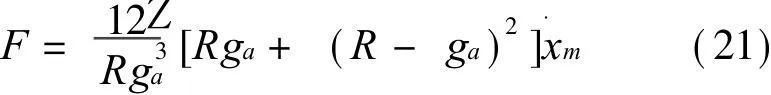
将式(21)的结果分别代入式(19)和(17),得

将式 (22)和(23)代入式 (11),可得

式中 a=6R3-9R2ga+10Rga2-3ga3
将式 (21)代入式 (16),得

综合式(24)和 (25),并由式(1)将梁上 y位置点的振动加速度代入,得到梁在振动时减振器内磁性液体的流速如下

由于不可压缩流体中单位时间的能量耗散可以表示为[17]

其中vi和vk分别为流体运动速度在坐标xi和xk上的分量,V为流体的体积。而本文中只考虑永磁体和外壳间隙内磁性液体的流动,所以耗能也只发生在这些流动中,且忽略磁场对磁性液体粘度的影响,这样其能量耗散可以简化为
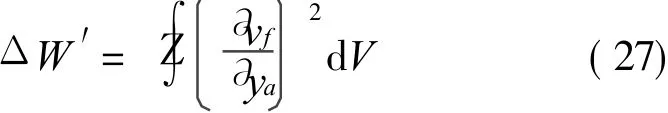
将式 (26)代入上式,并根据 d V=2πlm(ra+ ya)d ya,可得

其中

则在梁的振动周期 T内磁性液体的粘性耗能为

2.3 悬臂梁振动对数衰减率的计算
应用式(7),(4)和(30),可得到安装有磁性液体阻尼减振器的弹性悬臂梁振动的对数衰减率的表达式

其中Y和x0(y)分别由式(29)和 (2)给出。
3 实 验
在如图5(图6为其对应的实物图)所示的装置上进行实验研究。弹性悬臂梁选用黄铜板,尺寸为1 200mm× 50mm× 5mm,重 2.55 kg。 其一端固定,另一端安装磁性液体阻尼减振器,梁自由振动的频率k=1.74 Hz,实验时的初始振幅为15mm。固定在梁自由端的半导体加速度传感器可得到与振动加速度成定量关系的电压信号,该信号经数据采集器(DI-710)读入并经模数转换后输入到与之相连的计算机,数据采集器的采样频率为200 Hz。进入到计算机的信号首先转化为加速度数据,再由加速度数据得到梁振动的速度和位移数据。

图5 实验装置示意图Fig.5 Schemeo f the experimental devices

图6 实验装置实物图Fig.6 Graph of the experimental devices
为了验证所得理论的正确性,分别验证永磁体半径ra,永磁体和外壳间的间隙ga,以及不同饱和磁化强度磁性液体对悬臂梁振动对数衰减率的影响。阻尼减振器的结构参数和磁性液体的物理参数在表1中给出。其中永磁体的材料均为Nd-Fe-B,长度都为12mm,所用磁性液体的基载液均为煤油,其中分散的均为 Fe3 O4磁性颗粒。组装完成的减振器最重19.93 g。

表1 实验参数Tab.1 Experimental param eters
在以上条件下,一种振动的位移图像如图7所示。

图7 悬臂梁自由端的振幅变化曲线Fig.7 Diagrams of the plate oscillations with and without the damper
4 实验结果分析
图8中给出梁振动的对数衰减率Λ随永磁体半径ra变化的理论曲线和实验结果的对比。从图中可以看出,当永磁体半径较小时,实验结果与理论预测的一致性很好,而当永磁体半径较大时,一致性较差,而且理论曲线与实验值的偏差随着永磁体半径的增大而增大。这是因为当永磁体半径较大时,永磁体磁场对磁性液体的吸引力也较大,这种吸引力使得在包围永磁体周围形成超出永磁体尺寸较多的哑铃状磁性液体包覆层,如图9所示,这将阻碍外壳和永磁体间间隙内磁性液体的流动,而理论上这种影响在假设中忽略。图8还可以说明当永磁体半径较小时,梁振动的对数衰减率随着永磁体半径的增大而增大。

图8 梁振动对数衰减率随永磁体半径的变化Fig.8 Dependence of the logarithmic decay rate on theradius of themagnet

图9 吸引磁性液体后的永磁体Fig.9 The ferrofluid structure around themagnet
图10中给出梁振动的对数衰减率Λ随永磁体和外壳间的间隙 ga变化的理论曲线和实验结果的对比。可以看出,理论曲线与实验值的一致性在间隙较小时较好,较大时则较差。这是因为在推导理论是曾做出间隙与永磁体尺寸相比较小的假设,而在图中4个间隙较大的实验值中,间隙值已超过永磁体直径,理论中所假设的“薄层模型”已经不适用。从图10中还可以看出,在其他条件相同时,有一最佳的间隙值使得梁振动的对数衰减率达到最大。
将表1中的不同磁性液体按照饱和磁化强度从小到大编号为 1~5,在表2中给出使用这几种磁性液体时梁振动的对数衰减率理论值与实验结果的对比。从表中发现,使用1号磁性液体时理论值与实验结果的差别比其他磁性液体大。受重力的影响,减振器内永磁体会或多或少偏离外壳的轴线位置,而 1号磁性液体的饱和磁化强度最小,永磁体在外壳内处于同一位置时受到磁性液体的悬浮力也最小,所以偏离中心位置的距离就最大,而理论则是基于永磁体在磁性液体内居中的假设。
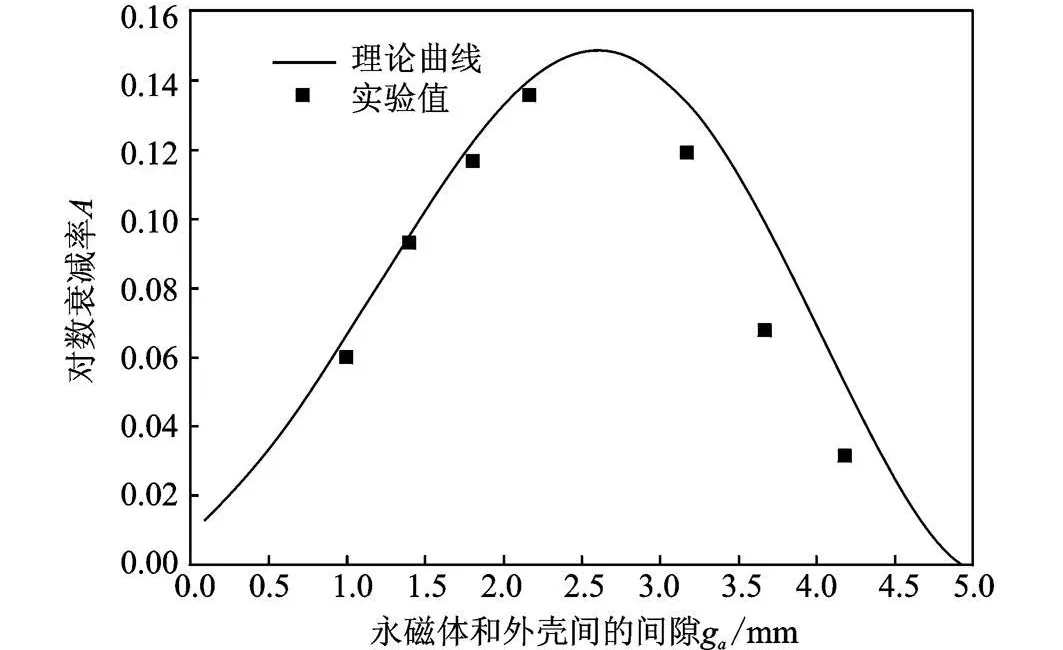
图10 梁振动对数衰减率随永磁体和外壳间间隙的变化Fig.10 Dependence of the logarithm ic decay rate on the wid th of the gap in the radial direction

表2 不同磁性液体时的对数衰减率Tab.2 The logarithm ic decay ratewhen dif ferent ferrof luid are used
5 结 论
(1)提出了一种结构简单的磁性液体阻尼减振器,建立了这种减振器的动力学模型,并结合弹性悬臂梁的振动能量,得到减振器施加于弹性悬臂梁后梁振动的对数衰减率。实验验证表明,在所假设的条件下,理论与实验结果的一致性较好。
(2)其他条件相同时,当永磁体半径较小时,磁性液体阻尼减振器的阻尼效果随着永磁体半径的增大而增大;减振器外壳与永磁体间有一最佳间隙,使得梁振动的对数衰减率达到最大。
[1] Rosensweig R E.The fascinating magnetic fluids[J].New Scientist,1966,20:146—148.
[2] Raj K,M oskowitz R.A review of damping applications of ferro fluis[J].IEEE Transactions on M agnetics,1980,Mag-16(2):358—363.
[3] Nakatsuka K,Yokoyama H,Shimoiizaka J.Dam per app lication of magnetic fluid for a vibration iso lating table[J].Journalof Magnetism and Magnetic Materials,1987,65:359—362.
[4] Fujita T,W ada Y,Obinata G,et a l.Comparison of frequency characteristics in a damper using magnetic fluid,ER fluid,ER fluid dispersing smec tite,and m ixed ERmagnetic fluid[J].International Journal of Modern Physics B,1996,10(23&24):3 001—3 010.
[5] Fujita T,Jeyadevan B,Yamaguchi K,etal.Preparation,viscosity and dam ping of functiona l fluids that respond to both magnetic and elec tric fields[J].Powder Technology,1999,101:279—287.
[6] Fukuda H,Ueno K,Kam iyama S,et al.Study on active damper with amagnetic fluid[J].JSM E Internationa l Journal Series B,1998,41(4):822—829.
[7] Kamiyama S,Okamoto K,Oyama T.Study on regulating characteristics of magnetic fluid active damper[J].Energy Conversion and Management,2002,43:281—287.
[8] Masato A,Yozo F,Shu ji K.Active tuned liquid damper(TLD)with magnetic fluid[A].Proceedings of SPIE-The International Society for Optical Engineering[C].1998,3329:620—623.
[9] Ohira Y,Houda H,Sawada T.Effect of magnetic field on a tuned liquid damper using a magnetic fluid[J].International Journal of Applied Electromagnetics and Mechanics,2001/2002,13:71—78.
[10]Horie S,SM anabu,Ohno K,et al.Effectivemethod of app lyingmagnetic field on a tuned liquid dam per using amagnetic fluid[J].Internationa l Journal of Applied Electromagnetics and M echanics,2007,25:139—143.
[11]BashtovoiV G,Kabachnikov D N,Ko lobov A Y.Research of the dynamics ofamagnetic fluid dynam ic absorber[J].Journal of Magnetism and Magnetic Materials,2002,252:312—314.
[12]Zhou G Y,Sun L Z.Smart co lloidal damperswith ondemand contro llab le damping capability[J].Smart Materials and Structures,2008,17:1—11.
[13]Liu J.Analysis of a porouselastic sheet damperwith a magnetic fluid[J].Journal of Tribology,2009,131:021801-1—021801-5.
[14]Rosensw eig R E.Fluidmagnetic buoyancy[J].A IAA Journal,1966,4(10):1 751—1 758.
[15]朗道,栗弗席兹著.弹性理论 [M].曹富新,译.北京:高等教育出版社,2009.L D Landau,EM Lifshitz.Theory of Elasticity[M].Beijing:Higher Education Press,2009.
[16]Rosensw eig R E. Ferrohydro dynamics [M]. New York:Dover Publications,Inc.Mineo la,2002.
[17]朗道,栗弗席茨著.流体力学 [M].孔祥言 ,徐燕侯,庄礼贤,译.北京:高等教育出版社,1983.L D Landau,E M Lifshitz.Fluid Mechanics[M].Beijing:Higher Education Press,1983.
