拍频激励下的冲击钻进机械系统动力学特性研究
2012-12-03苟向锋吕小红
苟向锋 吕小红
兰州交通大学,兰州,730070
0 引言
在机械工程应用领域中经常遇到冲击振动系统,如 冲 击 打 桩 机[1]、冲 击 钻 进 机[2-3]、夯 土 机[4]等。20世纪80年代以来,国内外学者开始用现代动力系统观点研究振动系统的动力学特性,研究内容也集中于振动系统的分岔、混沌问题,如研究系统的稳定性与分岔[5-7]、奇异性[8-9]、概周期碰撞运动[10]、倍周期分岔[11]等问题。文献[12-13]研究了以油作为介质建立的黏弹性模型的钻进运动。在实际工程应用中,如冲击钻探机一般采用高频率的外部冲击力来驱动钻头钻进,这种高频率的外部激励可以采用压电式换能器实现。但这种高频率的外部激励会使得系统的动力学行为更加复杂,而且系统在振动的同时伴随有钻进运动。文献[14]研究了一类冲击钻进机械振动系统的周期运动和分岔规律。该类系统的基本工作机理是滑块克服干摩擦力向下运动,因此,有限时间内的最佳钻进量对这类系统的有效工作非常重要。研究结果表明,在低激励频率范围内,系统呈现稳定的周期1单碰撞运动,且在周期1单碰撞运动速度的峰值附近,系统具有最佳钻进效果。文献[15]指出,低频激励所产生的稳定周期1振动—钻进运动可以用拍频激励的方式来实现。
近年来,冲击振动系统从实践角度得到了国内外学者的普遍关注,但同时考虑冲击振动和钻进运动的研究还较少。实际上,钻进运动对系统的振动是有影响的,这就要求建立考虑两种运动的综合性模型。本文建立了一类冲击钻进机械振动系统的力学模型,并考虑将高频低幅激励转化为低频高幅响应。这种转化要求冲击振动系统能够产生一种合理的内部作用力,以克服介质的阻力而产生钻进运动。
1 力学模型与运动微分方程
图1所示为冲击钻进系统的力学模型。2个不考虑质量的薄板组成运动基,其间距U可根据实际要求的激励模式随时间发生变化。运动基上板由刚度为K3的线性弹簧和阻尼系数为C3的线性阻尼器连接于质量块M2,质量块M2由刚度为K2的线性弹簧和阻尼系数为C2的线性阻尼器连接于质量块M1(含机架),质量块M1由刚度为K1的线性弹簧和阻尼系数为C1的线性阻尼器连接于滑块上,滑块的质量忽略不计。X1、X2、X3和X4分别表示滑块、质量块M1、质量块M2和运动基下板的位移,V表示运动基下板的速度。当质量块M2和质量块M1的位移差X3-X2=L时,质量块M2冲击质量块M1,假设该碰撞为塑性碰撞。碰撞后,两者或同步运动直至分离,或立即分离。质量块M2第i次冲击质量块M1以后,弹簧K1被压缩,对滑块产生向下的回复力。当作用于滑块的向下的回复力和阻尼力的合力大于干摩擦力F时,滑块向下运动,即系统发生钻进运动。滑块于本次冲击后瞬间钻进的深度为Li(i=1,2,…,n),整个系统于瞬间向下平移Li。当质量块M1向下运动的过程结束,开始向上运动时,滑块受到的弹簧回复力和阻尼力的合力小于干摩擦力F,滑块静止。此时滑块与土壤间的干摩擦力F由滑动摩擦力变为静摩擦力,滑块在土壤中不再发生滑移,直到下一次冲击来临为止。此刻滑块已钻进的深度为L1+L2+…+Li,并且不能回弹,即整个系统向下平移了L1+L2+…+Li。系统的静平衡位置相对滑块而言并没有改变。
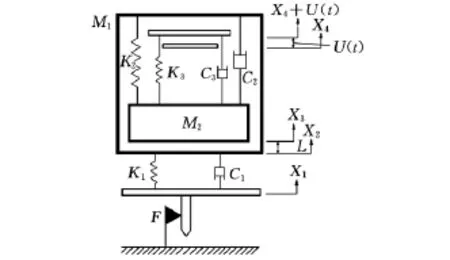
图1 冲击钻进系统的力学模型
系统最基本的功能是要能克服阻力(即干摩擦力)并向下移动。当质量块M2对质量块M1进行冲击后,滑块克服干摩擦力F向下移动。因此必须为运动基下板选择合适的运动形式才能使整个系统有效地向下移动。在运动基下板上加一个外力对系统的钻进运动并无益处,这相当于在质量块M2上直接加了一个外力,意味着实际中的高频激励是没有效果的。这样,就应该仔细选择运动基下板的运动形式。本文假定运动基下薄板的速度为一先验的确定函数V,其具体形式下文讨论。
分析质量块M2和M1在任意相邻两次碰撞间的运动过程。以振动体在重力作用下的平衡位置为原点,并设两质量块的碰撞时刻为系统运动的初始时刻。如果质量块M2冲击M1后,两者同步运动,则两者的加速度在此阶段是相同的,质量块M1和M2所受的合力分别为

由F1=F2/μm得

如果质量块M2冲击质量块M1后两者非同步运动,质量块M2和M1的加速度是不相同的。
式(1)和式(2)中,“·”表示对量纲一时间t求导,其中量纲一量为
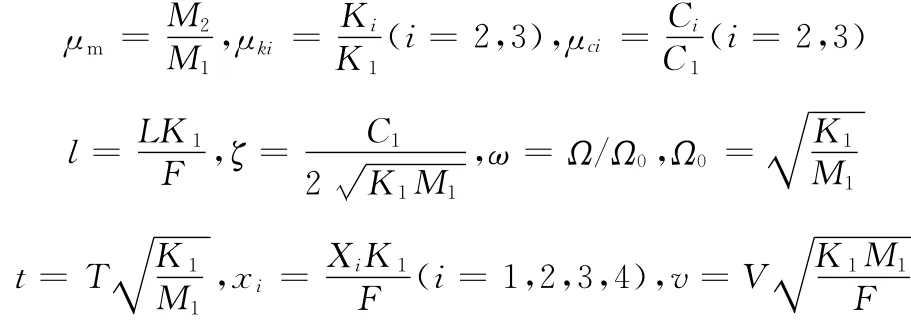
其中,Ω为频率,T为时间。
在任意的连续两次冲击之间,系统可能存在4种不同性质的运动状态:
(1)x3-x2>l,滑块静止,质量块M1和M2非同步运动,此时系统的量纲一运动微分方程可表示为

(2)x3-x2>l,滑块钻进运动,质量块M1和M2非同步运动,此时系统的量纲一运动微分方程可表示为
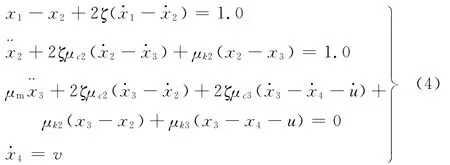
(3)x3-x2=l,滑块静止,质量块 M1和 M2同步运动,此时系统的量纲一运动微分方程可表示为

(4)x3-x2=l,滑块钻进运动,质量块M1和M2同步运动,此时系统的量纲一运动微分方程可表示为

质量块M2和M1的冲击方程为

其中,下标“-”“+”分别表示碰撞前后。
根据文献[15],其高频激励u(t)可表示为

其中,a=AK1/F,A 为幅值,ω 为高频,而 Δω=ΔΩ/Ω0为低频,要求等于固有频率,即Δω=1是为了满足共振条件。

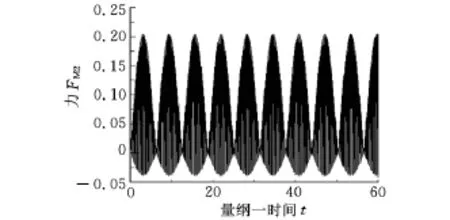
图2 施加于质量块M2的力
2 运动基下板速度函数

图3 质量块M2的时间历程图

选取量纲一参数:l=0.1,a=1.0,ζ=0.005,μm=0.25,μk2=0.1,μc2=0.1,μk3=0.2,μc3=0.2,ω=20。图1所示系统的时间历程如图4所示。由图4可见,在任意的连续两次冲击之间系统存在如下的运动过程:非同步运动→碰撞→同步运动→非同步运动→非同步运动伴随有钻进运动→非同步运动。随着系统钻进运动,位移值xi(i=1,2,3,4)的绝对值也会随之增大。此时,下板的位移x4等于滑块的位移x1。

图4 滑块、质量块M1和M2的时间历程图
现考虑驱动运动基下板所需的能量。当下板固定时,随着滑块钻进量的增大和质量块M2振动幅值A的增大,作用在运动基上的力的绝对值也增大。保持下板固定不动所需的外加量纲一载荷fext为

现在讨论控制下板运动的另一种替代方法。一旦外力fext达到某临界值fcrit,下板将被释放。但是,为了防止运动基出现不符合需要的大跳动,外力用一个系数β来减小,而非完全释放(fext=0),即
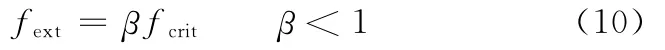
这可以通过下面的算法实现。假定下板的速度等于0,则外加载荷fext为
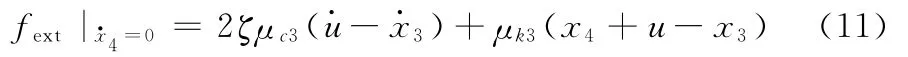
如果满足如下条件:

则下板的速度可由式(9)和式(10)决定:
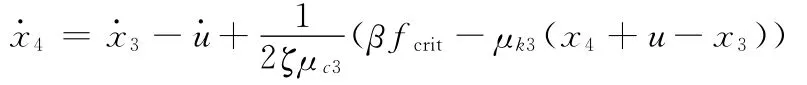
选取量纲一参数:l=0.1,a=1.0,ζ=0.005,μm=0.25,μk2=0.1,μc2=0.1,μk3=0.2,μc3=0.2,ω=20,fcrit=0.54和β=0.8。滑块、质量块M1、质量块M2和运动基下板的时间历程如图5所示。由图5可见,在任意的连续两次冲击之间系统存在如下的运动过程:非同步运动→碰撞→同步运动→非同步运动→非同步运动伴随有钻进运动→非同步运动。当作用于滑块的向下的回复力和阻尼力的合力大于干摩擦力F时,滑块向下运动,即系统发生钻进运动。下板的运动和滑块的运动并不一致,当下板静止时,滑块在质量块M1和M2碰撞作用下会发生多次钻进运动。图6为系数β分别等于0.8、0.75和0.7时下板的时间历程图,由图6可见,系数β越小,跳动次数越少,而跳动位移越大,但系数β对钻进效果的影响极小。

图5 时间历程图
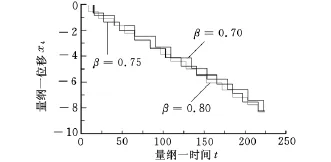
图6 运动基下板的时间历程图
3 结语
本文建立了一类冲击钻进机械系统的力学模型。为了使得系统能够发生钻进运动,且能够将高频低幅激励转化为低频高幅响应输出,选用了一种特殊的拍频运动激励。该拍频运动激励有两个主要特征:①低频调制激励与振动系统的固有频率(所期望的低频)吻合;②激励是非对称的,即只用调制波正值部分激励质量块M2。结果表明,该激励能够产生有效的冲击力即锤击效应。图1所示系统要求提供克服干摩擦力和形成稳定钻进运动的条件。在无控制的条件下有两种途径能够使得系统向下移动。但是,这些条件下得到的钻进量都比较小,有待于研究一种控制策略给系统提供额外的能量,以获得较好的钻进效果。
[1]Benamar A.Dynamic Pile Response Using Two Pile-driving Techniques[J].Soil Dynamics and Earthquake Engineering,2000,20:243-247.
[2]Wiercigroch M,Neilson R D,Player M A.Material Removal Rate Prediction for Ultrasonic Drilling of Hard Materials Using Impact Oscillators Approach[J].Physics Letters A,1999,259(2):91-96.
[3]Wiercigroch M,Krivtsov A,Wojewoda J.Dynamics of High Frequency Percussive Drilling of Hard Materials[M].Wiercigroch M,de Kraker B,eds.Nonlinear Dynamics and Chaos of Mechanical Systems with Discontinuities.Singapore:World Scientific,2000.
[4]Woo K C,Rodger A A,Neilson R D,et al.Application of the Harmonic Balance Method to Ground Moling Machines Operating in Periodic Regimes[J].Chaos,Solitons and Fractals,2000,11(15):2515-2525.
[5]Shaw S W,Holmes P J.A Periodically Forced Piecewise Linear Oscillator[J].Journal of Sound and Vibration,1983,90(1):129-155.
[6]Jin Dongping,Hu Haiyan.Periodic Vibro-impacts and Their Stability of a Dual Component System[J].Acta Mechanica Sinica,1997,13(4):366-376.
[7]Li Qunhong,Lu Qishao.Coexisting Periodic Orbits in Vibro-impacting Dynamical Systems[J].Applied Mathematics and Mechanics,2003,24(3):261-273.
[8]Whiston G S.Singularities in Vibro-impact Dynamics[J].Journal of Sound and Vibration,1992,152(3):427-460.
[9]Luo C J.Grazing and Chaos in a Periodically Forced,Piecewise Linear System[J].Journal of Vibration and Acoustics,2006,128:29-34.
[10]Luo Guanwei,Xie Jianhua.Hopf Bifurcations of a Two-Degree-of-freedom Vibro-impact System[J].Journal of Sound and Vibration,1998,213(3):391-408.
[11]Luo C J.Period-doubling Induced Chaotic Motion in the LR Model of a Horizontal Impact Oscillator[J].Chaos,Solitons & Fractals,2004,19:823-839.
[12]Pavlovskaia E E,Wiercigroch M,Grebogi C.Modeling of an Impact System with a Drift[J].Physical Review E,2001,64:056224.
[13]Pavlovskaia E E,Wiercigroch M.Two-dimensional Map for Impact Oscillator with Drift[J].Physi-cal Review E,2004,70:036201.
[14]Luo G W,Lv X H,Ma L.Periodic-impact Motions and Bifurcations in Dynamics of a Plastic Impact Oscillator with a Frictional Slider[J].European Journal of Mechanics-A/Solids,2008,27(6):1088-1107.
[15]Pavlovskaia E E,Wiercigroch M.Modelling of Vibro-impact System Driven by Beat Frequency[J].International Journal of Mechanical Sciences,2003,45:623-641.
