车-桥耦合系统MTMD振动控制参数研究

刘广波，周星德，石星星，张安乐

(1.河海大学力学与材料学院，江苏南京210098;2.河海大学土木与交通学院，江苏 南京210098)

0 引言

目前，车-桥系统的动力分析已经发展相对成熟，而振动控制策略的研究相对滞后，专门针对高速铁路车-桥振动控制的研究文献并不多见.

早期的国内外学者采用调谐质量阻尼器(TMD)对车-桥耦合振动系统的某一振型模态进行控制，有效地降低了桥梁在竖向的动力响应［1-3］.但随着列车时速不断提高，车桥耦合系统的共振问题日益突出，单一的MTMD控制系统已无法满足要求［4］.多频调谐质量阻尼器(MTMD)由多个小TMD组成，可以对系统的一段频率进行控制，对不同振型模态下的动力响应都有较好的控制效果［5-7］.MTMD相对于TMD具有多频调谐的优点，但MTMD需要较大的安装空间［8］，其参数选取也较为困难，如何合理地选取MTMD并设计其参数，从而实现对车-桥耦合系统的有效控制成为当前研究的一个课题.针对以上出现的问题，笔者对MTMD的参数设计进行了研究，给出了MTMD各项参数的选取方法和最优布置方案，改进了参数的设计方法，降低了经济成本，提高了控制的效率.

1 车-桥-MTMD系统振动方程

1.1 振动方程［9］

图1所示为车-桥-MTMD耦合振动系统，车辆简化为半车模型，采用二系悬挂.

图1 车－桥－MTMD系统截面Fig.1 Vehicle-bridge system cross-section

1.2 整体运动方程

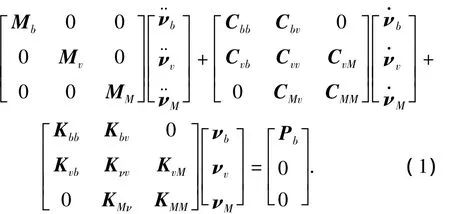
式中:Mb、Mν、MM分别为桥、车、MTMD 的质量矩阵;vb、vν、vM为桥、车、MTMD 的位移矩阵;Kbb、Kνν、KMM为桥、车、MTMD 的刚度矩阵;Cbb、Cνν、Cnm为桥、车、MTMD的阻尼矩阵.

1.3 竖向振动方程

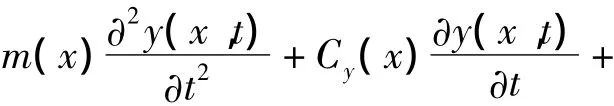
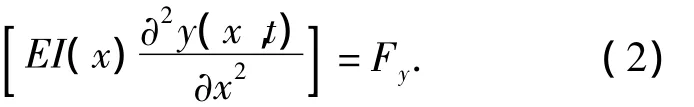
式中:m(x)为桥梁单位长度质量;Cy(x)表示桥竖向振动的阻尼;y(x，t)表示t时刻的竖向位移;E为弹性模量;I(x)表示截面惯性矩;Fy表示竖向作用力.

1.4 扭转振动方程

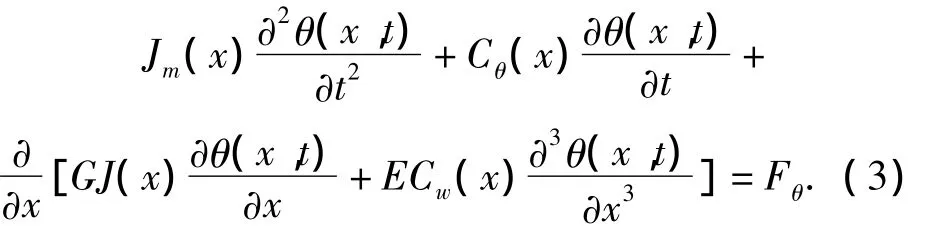
式中:Jm(x)为桥梁单位长度转动惯量;Cθ(x)表示桥转动方向阻尼;θ(x，t)表示t时刻的转角;G为剪切模量;J(x)表示转动惯性矩;Fθ表示扭转力.

1.5 MTMD的振动方程

跨中截面处第l个TMD的振动方程如下:

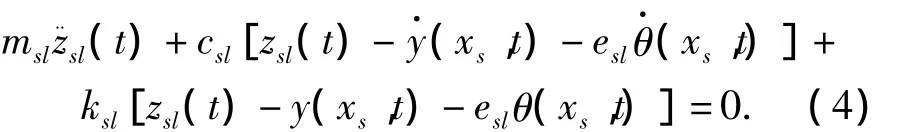
式中:msl表示第l个TMD的质量;csl表示第l个TMD的阻尼;ksl表示第l个TMD的刚度;zsl(t)表示第l个TMD的位移;esl表示第l个TMD到截面轴的距离;p为TMD的数量.

2 振动方程解耦

桥梁的竖向位移和转角为

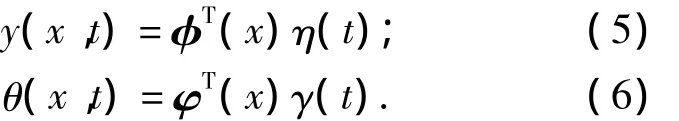
式中:φ、φ分别为竖向振型函数和扭转振型函数.

将式(5)、(6)带入方程式(2)、(3)并分别左乘φ、φ，对方程两边进行积分，得到解耦后的方程如下:

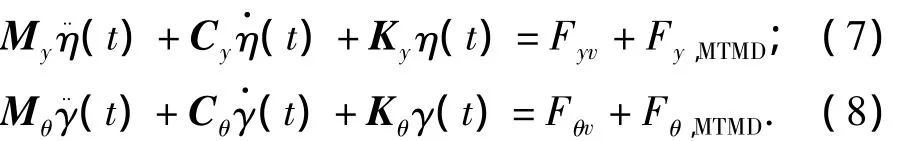
式中:My、Cy、Ky为N阶方阵，分别表示竖向模态下的质量、阻尼、刚度矩阵;Mθ、Cθ、Kθ为 N 阶方阵，分别表示转动模态下的质量、阻尼、刚度矩阵.

3 MTMD布置及参数设计

3.1 MTMD奇数布置法

研究发现控制器安装在受控模型位移峰值处时，结构的控制效果达到最优，笔者将MTMD安装在跨中截面处.

MTMD在布置时往往采取对称布置，对称布置又分为奇数对称布置和偶数对称布置，见图2.偶数对称布置法以截面对称轴为准，两侧对称安装TMD.奇数对称布置法首先在对称轴处安装TMD两侧依次布置，因此TMD的总数量要比偶数布置少，但频带宽度并未改变，因此二者的控制效果基本相同.

箱梁内部空间有限，安装和维修等都比较困难，因此MTMD中TMD的数量不宜过多.奇数对称布置法在保证控制效果的前提下具有较少的TMD，减少桥的附加质量以及TMD维护方面的问题，因此更加合理.

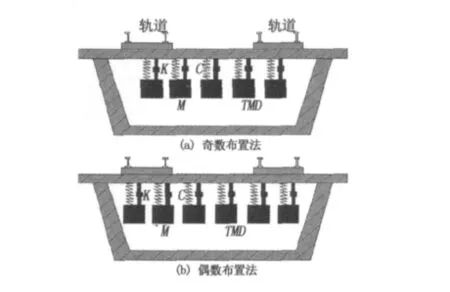
图2 奇数(偶数)对称布置Fig.2 Odd(even)symmetrical arrangement

3.2 MTMD最优频率

MTMD的特点就是多频调谐，频率的选取对控制效果有较大影响.

第j阶振型模态下TMD的频率比为

最优频率比可通过求解以下方程求得

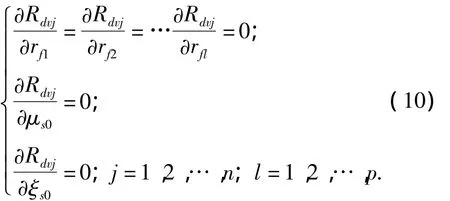
式中:Rdvj为第j阶模态的响应比函数.

最优频率的连续性越好，控制效果也就越好，因此在进行频率设计时要结合TMD的数量和最优频率特征值进行优化设计，频率设计应满足连续性好、频带宽度大的要求.

4 实例分析

4.1 计算参数

以台湾高速铁路桥为例进行仿真计算，桥长40 m，单位长度质量38 240 N·s2·m-2，截面惯性矩17.9 m4，单位质量极惯性矩464 500 N·s2，惯性扭矩35 m4，列车偏心距2.35 m，阻尼比2.5%，1～2阶竖向振动频率分别为22.54，90.24 rad/s，1～2阶扭转振动频率分别为 74.54，149.08 rad/s.列车采用法国TGV高速列车，车厢长度 18.7 m，列车时速 240 km/h，半车质量27 000 kg，转向架质量3 000 kg.

4.2 计算结果分析

4.2.1 扭转振动对动力响应的影响

由结果分析可知，考虑扭转效应后跨中位移比不考虑扭转效应的跨中位移增大，最大位移差达到0.6 mm，位移增大约24%，如图3所示.

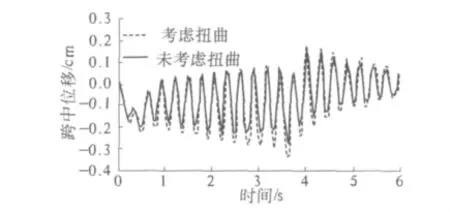
图3 动力响应曲线Fig.3 Dynamic responses curve

扭转效应对新型高速铁路桥梁的振动响应有较大的影响，因此对高速铁路桥梁进行动力分析应考虑扭转效应的影响.

4.2.2 MTMD减振效果

采用MTMD控制，跨中位移和加速度明显降低，MTMD控制取得了显著的控制效果，如图4所示.针对列车上桥和下桥时存在的峰值跳跃现象，采用MTMD-MTMD或MTMD-TMD混合控制的方法进行控制，将取得较好的效果.

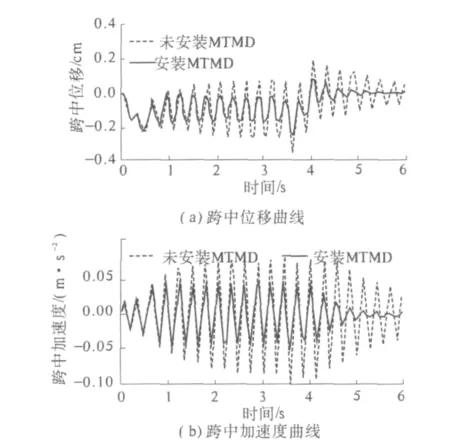
图4 跨中位移和加速度时程曲线Fig.4 Midspan displacement and acceleration curve

4.2.3 计算模态数及频率取值

结构的模态数对结构的位移有较大影响，考虑较高的模态数能使结果更精确，但相应的计算量也会增加.研究发现，高阶模态下的响应对结果影响较小，可以取较少的模态数进行计算.取模态数N为2和20计算，竖向与扭转位移曲线见图5.

对峰值处的位移进行误差分析，最大误差为0.05 mm.N=2相比N=20结果只减小了2.4%，但计算时间由38 s降低到2 s，这对于高速铁路的实时控制有较大的意义.笔者建议在进行仿真计算时可仅考虑前两阶模态.

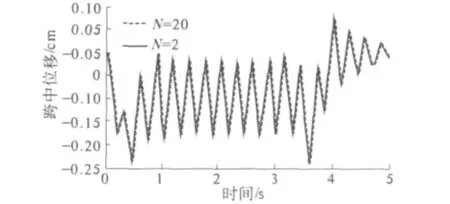
图5 模态数N=2，N=20竖向位移曲线Fig.5 Vertical displacement curve with modal number N=2，20

由式(9)可知TMD的频率由结构固有频率来确定.实际设计中rfl取值范围介于0.75～1.25之间，ωyj随着阶数的增高会急剧变大，这对于TMD设计来讲是比较困难的.高阶模态下的动力响应对结果的影响不大，因此可根据结构的低阶频率来确定小TMD的频率.通过研究发现MTMD的频率应根据第一阶模态来确定.

则式(9)改写为:

4.2.4 奇数布置法控制效果

当列车过桥时，奇偶布置方法取得的控制效果基本相同，最大误差仅为0.003 mm，见图6.偶数布置法比奇数布置法安装的TMD数量多，导致桥的附加荷载增大.采用奇数布置法既能保证控制效果，又能节约成本，具有工程实用价值.因此，采用奇数布置法来布置MTMD更合理.

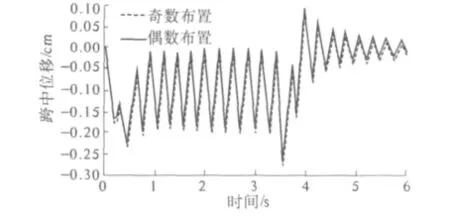
图6 MTMD奇偶布置位移曲线Fig.6 Displacement curve with odd and even MTMD

5 结论

(1)扭转振动对结构稳定性有较大影响，在进行动力分析时应考虑扭转效应.

(2)高阶模态下车-桥系统的振动响应较小，在进行仿真计算时可取较少的模态数进行仿真计算，这样可以大大减少工作量和计算时间，同时又能保证计算结果的精度.

(3)MTMD奇数对称布置法设计更为合理，具有较大的工程意义.高阶模态对计算结果影响较小，MTMD频率应根据第一阶频率来进行设计.

［1］ KWON H C，KIMMC，LEE I W.Vibration control of bridge under moving loads［J］.Computer＆ Structure，1998，66(4):473-480.

［2］ WANG J F，LIN C C.Vibration suppression for highspeed train bridge using tuned mass dampers［J］.International Journal of Solids and Structures，2003(40):465-491.

［3］ LIN CC，WANG JF，CHEN B L.Train-induced vibration control of high-speed railway bridges equipped with tuned mass dampers［J］.Journal of Bridge Engineering，2005，10(4):398-414.

［4］ WU J D，YANG Y B.Vibration reduction for cablestayed bridges traveled by high-speed train［J］.Finite Elements in Analysis and Design，2004(40):341-358.

［5］ YANGY B，CHANGCH，YAU JD.Element for analyzing vehicle-bridge systems considering vehicle pitching effect［J］.International Journal for Numerical Methods in Engineering，1999，46(7):1031-1040.

［6］ 肖艳平.桥梁振动控制的初步研究［D］.成都:西南交通大学土木工程学院，2006.

［7］ 郭文华，路萍.TMD对高速列车通过简支箱梁时的振动控制研究［J］.振动与冲击，2010，27(11):42-45.

［8］ 杨宜谦，张锻.用调频质量阻尼器抑制铁路桥梁竖向共振的研究［J］.中国铁道科学，1998，3(1):12-18.

［9］ 潘家英，高芒芒.铁路车-线-桥系统动力分析［M］.北京:中国铁道出版社，2008.