基于两类结构形式的索梁锚固区力学行为分析

高小妮，贺拴海，宋一凡

(1.交通运输部公路科学研究院，北京100088;2.长安大学桥梁与隧道陕西省重点实验室，陕西西安710064)

0 引言

锚固区是索梁之间的重要传力构件，是缆索体系重要的构造之一.目前，对于吊杆锚固区局部分析多采用有限元数值模拟进行研究.大量国内外学者对锚固区应力分布情况［1-4］、边界条件［5-6］和极限承载能力［7-8］等进行了有限元数值模拟.可见，在缆索体系桥梁中，锚固区结构的应力、变形及稳定性等应进行专门的分析研究.

对锚固区结构进行有限元分析时，锚固区节段长度选取的合理性关系着计算结果的准确性，选取节段长度时既要遵守圣维南原理保证计算结构的准确性，又要尽量节省计算时间，避免资源浪费.而在实际有限元模拟分析中节段长度的选取存在着分歧.因此，笔者依据某在建缆索桥锚固区构造特点，采取横桥向和顺桥向2类锚固区构造形式，选4种锚固区节段长度，建立8个模型进行有限元分析.通过对比分析不同节段长度对不同锚固构造形式的锚固区结构应力、变形和稳定特性的影响，并针对构件的分析要点，提出合理的锚固区节段长度的选取，为今后锚固区空间分析及模型试验提供参考.

1 基本理论和方法

1.1 非线性基本理论和方法

1.1.1 几何非线性

笔者在锚固区阶段分析时考虑了结构几何非线性的影响，单元刚度矩阵［9］为

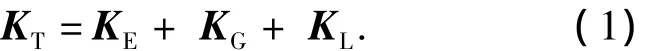
式中:KT为切线刚度矩阵;KE为小位移的线性刚度矩阵;KG为初应力矩阵或几何刚度矩阵;KL为初始位移矩阵或大应变矩阵.

1.1.2 材料非线性

(1)钢材的本构关系.以往大量研究表明，钢材具有良好的塑性性能，一般将钢材的力学模型简化为理想弹塑性体.

(2)屈服准则.Von Mises屈服准则是一个比较通用的屈服准则，尤其适用于金属材料.本文研究对象为吊杆锚固区，其主要材料为钢板，因此选用Von Mises屈服准则.对于 Von Mises屈服准则，其等效应力为［10］:

式中:σe为 Von Mises应力;σ1，σ2，σ3为 3 个方向主应力.

1.2 弹性稳定分析基本理论

结构稳定问题分为分枝点失稳、极值点失稳和跳跃失稳三类.对分枝点失稳进行分析.

根据最小势能原理可知势能的一阶变分等于零，于是得到:

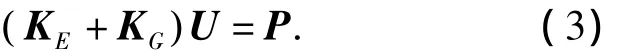
式中:U为节点位移向量;P为节点荷载向量.

如果P增大为λP时，KG也将增大λ倍，则式(3)可表示为

如果此时结构达到临界状态，则必然存在一扰动的位移使得系统在外力不变的条件下亦处于平衡状态，该位移设为U+ΔU，因此有:

由式(5)减去式(4)得到:

对于任何一个{ΔU}都满足式(6)，则必有:

将式(7)写成特征方程为:

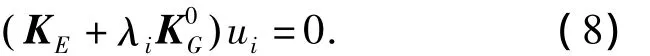
式中:λi和ui分别表示各阶稳定特征值的大小和相应的失稳形态.在工程中所关心的是最小特征值的问题，因此，由式(7)可求得最小特征值λcr，则其临界荷载为λcrP.

2 研究背景

2.1 工程概况

以某斜拉-自锚式悬索组合体系桥为依托工程.该桥全长555 m，为三塔斜拉自锚式悬索组合体系桥，包括主塔斜拉索体系段与自锚式悬索体系段.自锚式悬索体系段为自锚式悬索组合斜拉索背索结构体系，由主缆、柔性斜吊杆、刚性钢吊杆和斜拉背索组成，该桥桥型布置见图1所示.

2.2 锚固区构造

根据锚固区构造特点及传力特性，锚固区初设采用2种构造方式，除了传统的横桥向设置锚固区外［11］，本依托工程另采用锚固区顺桥向设置，如图2所示.锚固区顺桥向设置其传力途径是钢锚箱将索力传递到钢锚梁，钢锚梁将荷载传递给横隔板，最后由横隔板将力传递到腹板.

3 吊杆锚固区有限元分析模型

3.1 有限元模型

有限元分析软件采用大型结构通用软件ANSYS，选用壳单元，并结合两种锚固区构造及不同锚固区节段长度，共建8个有限元模型，有限元模型的确定如表1所示.

表1 有限元模型的确定Tab.1 Determination of finite element models

3.2 边界条件及荷载确定

由于主梁构造及材料均沿主梁中线对称，因此计算模型取1/2模型进行分析.在局部模型分析时，采用应力边界条件与位移边界条件.作者采用应力边界条件.

对全桥整体分析后，在最不利荷载组合下，第4根吊杆处吊杆力最大，选取该吊杆对应的锚固区为分析对象.考虑到锚箱垫板的分配作用，作用荷载根据锚箱垫板的尺寸均布作用于锚箱底板上.

4 计算结果分析

4.1 应力计算结果分析

4.1.1 钢锚箱应力比较分析

通过分析各模型锚固区钢锚箱部件应力分布情况，可以判断最大应力发生在钢锚箱底板，限于篇幅，钢锚箱底板应力分布仅给出Von Mises等效应力分布，如图3所示.为了进一步说明不同模型计算情况的差异，给出了钢锚箱最大应力的数值，如表2所示.

由图3及表2钢锚箱分析可见:

(1)锚固区横桥向设置时，由等值线图可见，钢锚箱底板受力均匀，应力集中现象发生在底板与侧板焊接的部位，应力集中范围较小.相同部位应力分布基本一致，且数值接近.模型1的6级等值线与其余3个模型的数值相差较大，B、C级应力分布情况与其余模型相同级别的应力分布情况有明显差异.

(2)锚固区顺桥向设置时，由等值线图可见，钢锚箱底板受力较均匀，应力集中范围较小.等效应力主要集中在6～55 MPa范围内.由应力等值线可反映出相同位置应力分布情况基本一致，且数值较接近.

(3)锚固区横桥向设置时，由表2可见，模型1应力计算结果最大，模型2最小，模型3和模型4的计算结果相同.

(4)锚固区顺桥向设置时，由表2可见，4个模型中最大主拉应力相差0.1 MPa，最大主压应力相差0.1 MPa，等效应力相差0.1 MPa.

图3 钢锚箱底板Von Mises应力分布图(单位:N/m2)Fig.3 Von mises stress distribution of steel anchor box bottom

表2 钢锚箱最大应力Tab.2 The maximal stress of steel anchor box MPa

4.1.2 钢锚梁应力分析

通过分析各模型锚固区钢锚梁部件应力分布情况，给出钢锚梁的最大应力，如下表3所示.(1)锚固区横桥向设置时，由表3可以看出:1)最大主拉应力分析结果中，模型1计算值较其它3个值小，其余3个模型计算数据相差较小;

表3 钢锚梁最大应力Tab.3 The maximal stress of steel anchor beam MPa

2)最大主压应力分析结果中，计算结果相差不大.

3)等效应力分析结果中，模型1计算值较模型4相差2.3%，较模型2相差2.5%.模型3与模型4计算值一致.

(2)锚固区顺桥向设置时，由表可以看出:

1)最大主拉应力分析结果中，模型5较其它3个模型应力值小.模型7和模型8计算结果一致.

2)最大主压应力分析结果中，模型6较模型5大28.5%，较模型7和模型8小一些.

3)等效应力分析结果中，模型7和模型8计算值较模型5大19.4%，较模型6大一些.

可见，锚固区横桥向设置时，模型1与其余3个模型计算结果差别较大，模型3和模型4计算结果一致.锚固区顺桥向设置时，模型5和其余3个模型计算结果差别较大，模型7和模型8计算结果一致.

4.2 变形计算结果分析

在相同荷载作用下，各计算模型节段横桥向、顺桥向及竖向最大变位，如表4所示.

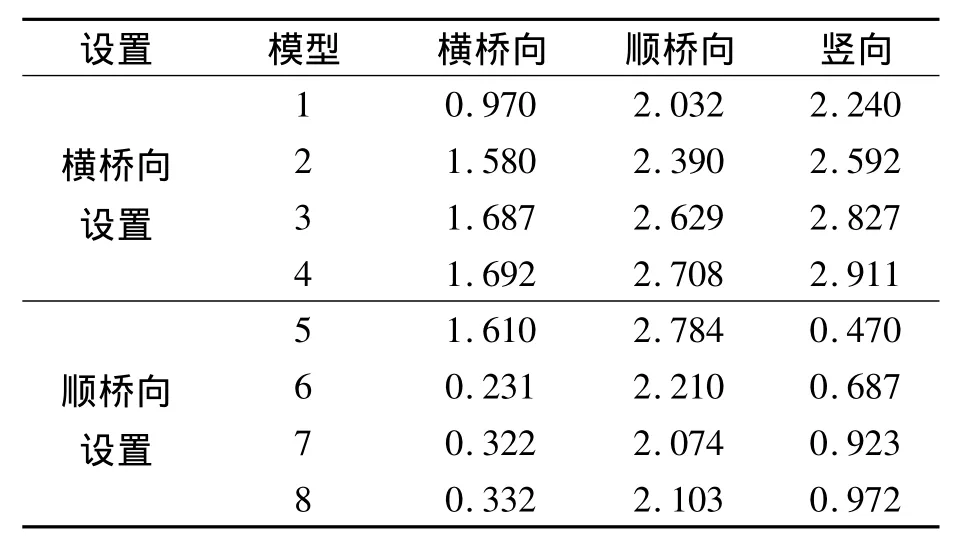
表4 节段整体最大变位Tab.4 The maximal deformation of overall segment mm

锚固区横桥向设置时，即模型1～模型4.由表4可见，模型2横桥向变位较模型1增大62.9%，模型3较模型2增大6.8%，模型4较模型3增大0.3%;模型4顺桥向变位最大，较模型3增大3%，较模型2增大13.3%，较模型1增大33.3%;模型1～模型4竖向变位随着模型节段增加在不断增大，模型4较模型3大3.0%.

锚固区顺桥向设置时，即模型5～模型8.由表4可见，锚固区节段整体横桥向、顺桥向和竖向的变形中，模型5和模型6的变位与其它两组数据相差较大.

可见，锚固区节段的变形随着节段长度的增加，变形趋于稳定，受边界影响逐渐减弱，计算结果可靠.

4.3 特征值屈曲分析

通过ANSYS软件对8个模型进行第一类稳定性计算分析，其计算结果如表5所示.从特征值计算结果可见:

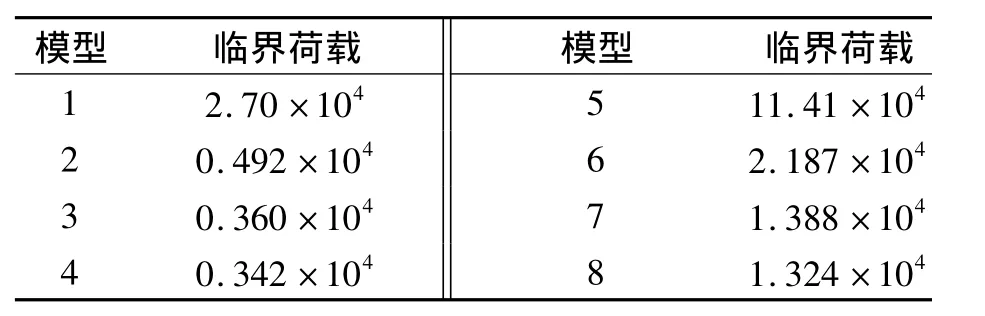
表5 8种模型临界荷载Tab.5 The critical loads of eight models MPa

(1)锚固区横桥向设置，模型4的临界荷载较模型1减小87.3%，较模型2减小30.5%，较模型3减小5%.模型4和模型3计算结果较接近.可见，随着锚固区节段的增长，计算结果逐渐趋于稳定.

(2)锚固区顺桥向设置，模型8的临界荷载较模型5减小88.4%，较模型6减小39.5%，较模型7稍小.模型7和模型8计算结果较接近，即选取远离锚固区2倍梁高的节段，可较准确反映结构的整体稳定特性.

5 结论

(1)钢锚箱的应力分布情况受锚固区节段长度的影响较小，为了使计算结构合理化，建议在对钢锚箱应力分析时，锚固区域长度应至少选取远离锚固区1倍梁高的节段.

(2)不论锚固区选取何种形式设置，钢锚梁的应力情况受锚固区节段影响较大，当模型节段选取远离锚固区2倍以上梁高的计算长度时，应力情况基本趋于稳定，边界对计算结果的影响较小.

(3)锚固区节段变位受节段长度影响明显.当锚固区节段选取远离锚固区2倍梁高时，结构整体变位趋于稳定，随着节段长度增大，结果计算差值在5%之内.

(4)对锚固区一类稳定对比结果表明，不论锚固区采用何种方式设置，对锚固区建立有限元稳定性分析模型时，模型节段应至少选取远离钢锚梁2倍梁高的长度.

［1］ 刘庆宽，强士中，张强，等.斜拉桥锚箱式索梁锚固区应力分析［J］.桥梁建设，2001(5):14-16.

［2］ 韩富庆，杨成斌，娄建，等，安庆长江公路大桥索塔锚固区受力分析［J］.合肥工业大学学报:自然科学版，2002，26(6):1167-1170.

［3］ 彭苗，陈升平，余天庆，等，巴东长江大桥索塔锚固区节段模型试验与空间应力分析［J］.武汉理工大学学报，2004，28(5):759-7620

［4］ 熊刚，谢斌，黄思勇，等，天津保定桥索塔锚固区钢锚箱空间分析［J］.华中科技大学学报:城市科学版，2009，26(4):80-83.

［5］ 万臻，李乔，毛学明.大跨度斜拉桥钢锚箱式索梁锚固结构空间有限元模型比较研究［J］.四川建筑科学研究，2006，32(1):26-31.

［6］ 彭霞，王行耐.钢锚箱式索梁锚固区段有限元仿真分析［J］.公路，2009(9):28-33.

［7］ 狄谨，周绪红，游金兰，等，钢箱梁斜拉桥索塔锚固区的受力性能［J］.中国公路学报，2007，20(4):48-52.

［8］ 吴冲，韦杰鼎，曾明根，等.上海长江大桥斜拉桥索梁锚固区静力试验研究［J］.桥梁建设，2007(6):30-33.

［9］ 朱伯芳.有限单元法原理与应用［M］.北京:中国水利水电出版社，2009.

［10］孙训方，方孝淑，关来泰.材料力学［M］.北京:高等教育出版社，2002.

［11］郑刚，王天亮.猎德大桥吊索锚箱传力和疲劳性能试验方案设计［J］.世界桥梁，2009(1):49-52.