钢丝绳缺陷检测励磁结构尺寸设计
2012-12-02李万莉冯文洁李珍珍颜崇浙
李万莉,冯文洁,李珍珍,颜崇浙
(同济大学 机械与能源工程学院,上海201804)
钢丝绳无损检测是一个理论性、实践性和综合性较强的课题,涉及到励磁结构设计、传感器设计、数字信号处理、定量检测的模式识别等领域的研究.钢丝绳绝大多数采用导磁性能良好的高碳钢制成,很适合于利用电磁检测法进行检测,同时电磁检测法具有成本较低、易于实现等优点,也是目前公认的最可靠的钢丝绳检测方法[1].而且,目前实用的钢丝绳技术和仪器几乎都采用电磁检测法[2-4],本文的钢丝绳缺陷检测也是基于电磁检测法.电磁检测法以钢丝绳被检测段达到一定的磁化强度为前提,即达到一定的磁饱和状态,文中论证了钢丝绳磁化状态需达到一定的磁化强度且励磁结构的尺寸对钢丝绳的磁饱和状态有决定性影响.目前,在考虑励磁结构尺寸达到设计要求以及励磁结构磁源的利用率的基础上,关于励磁结构尺寸设计基本处于定性的角度,很少研究励磁结构尺寸与钢丝绳的磁饱和状态的因果关系.本文提出以钢丝绳能否磁化到一定的磁化强度作为励磁结构设计合理性的依据,在考虑不同形态的边界形状,尤其对于非线性、多层媒质的磁场和材料的非线性磁特性,采用数值解法——有限元方法对励磁结构有限元模型进行精确求解,得出励磁结构尺寸的变化对钢丝绳磁化强度的影响并得出影响钢丝绳磁饱和状态的关键尺寸.而且,钢丝绳缺陷检测励磁结构尺寸设计的数值解法——有限元方法对其他相关领域的无损检测技术同样具有较普遍的理论意义和应用价值.
总之,用电磁检测法对钢丝绳进行无损检测,首先要保证钢丝绳被检测段磁化到一定的磁饱和状态;其次要尽可能地提高磁源的利用率,使励磁结构尽可能轻、小,使磁源提供的能量尽可能地引入到钢丝绳被检测段中.为了达到以上2个要求,钢丝绳缺陷检测励磁结构尺寸设计过程包括:①钢丝绳磁化强度选择;②励磁结构尺寸的理论设计;③励磁回路ANSYS仿真;④根据励磁回路仿真的结果调节尺寸参数确定励磁结构最终设计尺寸.
1 钢丝绳无损检测励磁结构模型
在钢丝绳的缺陷检测和诊断实践中,通常根据钢丝绳上缺陷的不同性质和状况将钢丝绳损伤分为两大类:局部缺陷型(localized fault,LF 型)和截面积 损 失 型(loss of metallic cross-sectional area,LMA 型).对LF 型缺陷的检测采用基于霍尔元件的漏磁通法[5],对LMA 型缺陷检测采用磁桥路法[6].钢丝绳无损检测励磁结构模型集成了对LF型和LMA 型的检测,根据2种缺陷的形式设计的钢丝绳无损检测励磁结构模型如图1所示.
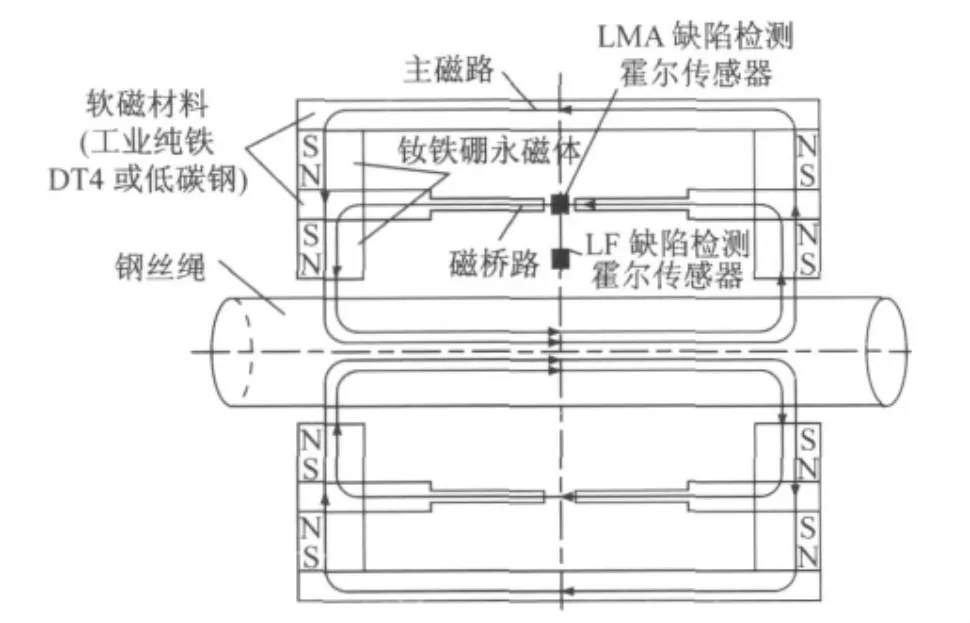
图1 钢丝绳无损检测励磁结构模型Fig.1 Wire rope nondestructive testing excitation structure model
2 钢丝绳磁化强度选择
钢丝绳的相对磁导率μrw随钢丝绳被磁化的程度非线性变化[7],如图2所示,图中H为磁场强度,B为磁感应强度,μ0 为真空磁导率,Hμm为磁导率取最大值时的磁场强度,Pm为钢丝绳最大磁导率点.
选择钢丝绳的初度饱和区作为钢丝绳要达到的磁化强度可使检测信号中获得最佳的断丝检测信号的信噪比[7],且与深度磁饱和相比,这一磁化要求会极大减小励磁结构的体积、质量.
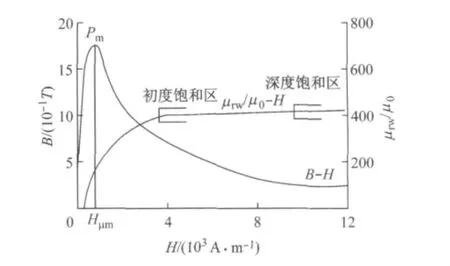
图2 钢丝绳典型磁化特性Fig.2 Wire rope typical magnetize characteristic
2.1 磁化强度对局部缺陷型检测信号的影响
考虑单丝断口漏磁场,根据磁荷分析理论,可假设断丝两端各有一磁荷,建立计算漏磁场分布的数学模型,如图3所示,图中,P(x,y)为坐标平面的任何一点,P1和P2为磁荷;r,r1,r2分别为P(x,y)到O(0,0),P1(-l,0),P2(l,0)的距离;d为钢丝绳直径;2δ为断口间隙;2l为磁荷间的距离.断丝断口产生的漏磁场可由这一假想的磁荷定性和定量解释.
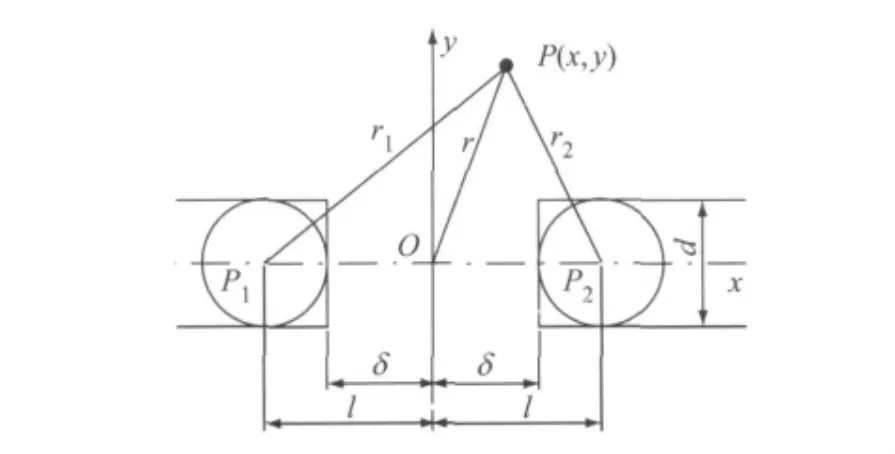
图3 断丝漏磁场磁荷解释模型Fig.3 Interpretation model of magnetic charge for broken wires leakage magnetic field
据磁场理论,磁荷Q与钢丝绳被磁化后的磁感应强度Bw和等效磁荷直径ds有关,可认为[7]:Q=,其中ds与断丝类型、端口形状有关.检测漏磁场的磁感应强度采用霍尔传感器,其输出电压VH与信号磁感应强度有如下关系:VH=KcIcBw·cosφ,式中:Kc为霍尔传感器的灵敏度系数;Ic为霍尔传感器输入的控制电流;φ为磁感应强度与元件法向矢量之间的夹角.可以看出,传感器输出幅值与漏磁场的磁感应强度成比例,因此,为了提高检测的灵敏度,应在损伤条件相同的情况下尽可能加大漏磁场的值,钢丝绳应被饱和磁化.
2.2 磁化强度对截面积损失型缺陷信号的影响
在不考虑漏磁的情况下对图1励磁结构磁化回路进行分析,可将其等效为以下磁路模型[7],如图4所示,其中,Rx1~Rx6为衔铁磁阻;Rk1~Rk6为空气隙磁阻;F1~F8为磁源磁势;Rg为钢丝绳磁阻;1/2Φx,1/2Φm,1/2Φg分别为通过Rx1,Rk1,Rg的磁通量;Rm,Rw分别为Rx2+Rk1+Rx3和Rk2+Rg+Rk3.
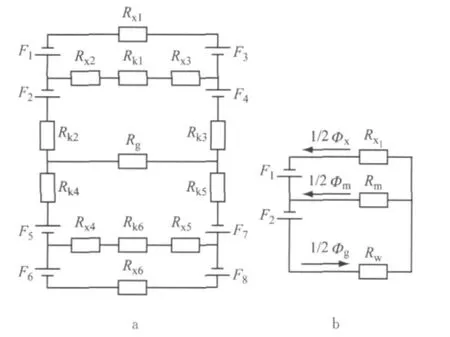
图4 励磁结构磁化回路等效模型Fig.4 The equivalent circuit model of excitation structure
根据磁通连续原理和磁路基尔霍夫定律可以得到如下方程组[8]:解方程组得Bm,并对Rg求导后得
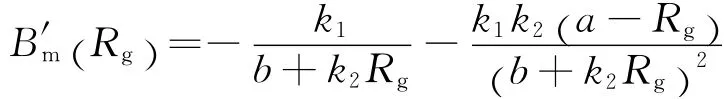
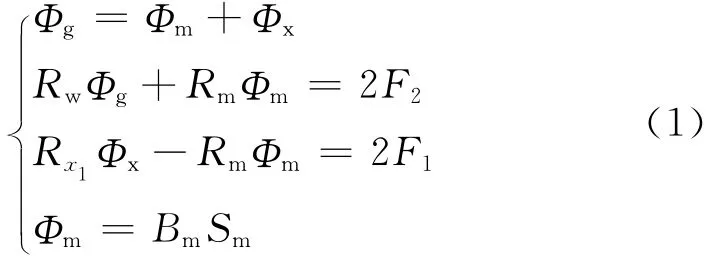
式中:k1,k2分别为2/(F1Sm)和Rx1+Rm;a,b分别为(F2/F1)Rx1-Rk2-Rk3和Rx1Rm+(Rx1+Rm)·(Rk2+Rk3).因为磁桥路法在钢丝绳没有产生LMA缺陷时要尽量保证通过磁桥路的磁通量为零,即使,此时钢丝绳的磁阻Rg也最小.由此可见a>0,而b,k2也均大于零,磁桥路磁感应强度的大小Bm(Rg)及磁感应强度变化率B′m(Rg)随Rg变化的趋势如图5.
通过分析图5可知,BmR(g)随着Rg的增大而减小也随着Rg的增大而减小,由磁阻计算式Rg=lg/(μgSg)可知钢丝绳的磁化应选择其磁导率较大的点,即钢丝绳典型磁化特性曲线中的Pm点,其中lg,μg,Sg分别为钢丝绳轴向被磁化段的长度、磁导率和横向截面积.
总之,为了得到较好的信噪比、减小励磁结构的体积和重量以及使钢丝绳被充分磁化,选择钢丝绳磁导率最大点Pm右侧初度饱和区作为钢丝绳磁化磁场强度的选择区间.
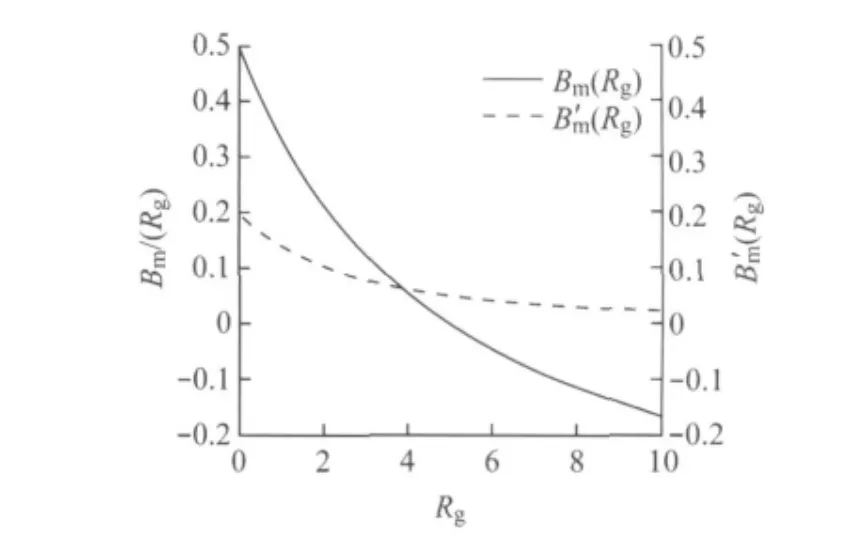
图5 Bm (R g ),B′m (R g )随Rg 变化曲线Fig.5 Variations curves of Bm (R g )and B′m (R g )with Rg
3 励磁结构尺寸的理论设计
3.1 励磁结构尺寸参数设计及理论计算
以下以直径36 mm 的钢丝绳分析各结构尺寸对钢丝绳缺陷检测的影响,励磁结构尺寸参数如图6,其中Lm为永磁体沿钢丝绳轴向的长度;Lg为两衔铁间沿钢丝绳轴向的间隙;Ls为两永磁体内侧面间沿钢丝绳轴向的距离;q为永磁体内侧面与钢丝绳表面间径向距离;Ds为钢丝绳的直径;Tx1,Tx2分别为外、内衔铁厚度;Tm1,Tm2分别为外、内永磁体厚度.
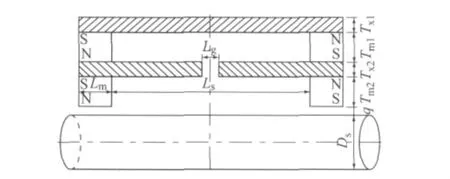
图6 励磁结构尺寸参数Fig.6 Design parameters of excitation structure size
由图6中的励磁结构计算最外衔铁磁阻Rx1,桥路磁阻Rx2,Rx3,钢丝绳磁阻Rg,钢丝绳气隙磁阻,磁势
励磁回路为非线性的磁化回路,磁路中存在铁磁性材料,其磁导率随着磁场强度非线性变化,上述方程为非线性方程组,需要应用数值解法确定永磁体的工作点和铁磁性材料的磁导率,采用逐步逼近的方法计算.
首先假定一个钢丝绳的磁化状态Hg和Bg,根据磁通连续原理,通过内永磁体的磁通与通过钢丝绳的磁通相等,即B2S2=BgSg,S2=2πl·Lm,其中,Bg为钢丝绳磁化状态的磁感应强度;Hg为钢丝绳磁化状态的磁场强度;B2为内永磁体的磁感应强度;S2为内永磁体径向圆周面积;l为内永磁体径向周长.根据假设的已知钢丝绳磁化状态可以算出B2.
选择永磁体材料为钕铁硼N35,由于其退磁曲线接近直线,因此可按下列直线方程来计算:B=Br(1-H/Hc),其中,Br为材料的剩余磁感应强度;Hc为材料的矫顽力.因此可以求解出内永磁体在该状态下所提供的磁势F2。
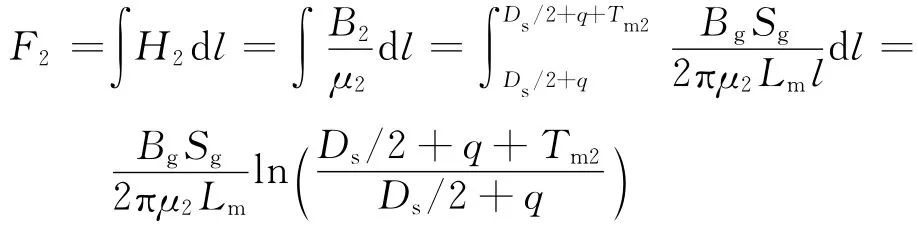
式中:H2为内永磁体的磁场强度;μ2 为内永磁体的磁导率.得到F2后,可以根据方程组(1)中的第2个方程求解磁桥路的磁化状态Hxq和Bxq.其中已知条件为Rw,Φg和F2,而Rm=Rx2+Rk1+Rx3,Φm=与μxq有关,μxq为磁桥路的磁导率,Φm与Bxq有关,μxq与Bxq之间存在非线性关系[9],因此该方程也是一个非线性方程,采用二分法和线性插值的方法求解,通过变换方程RwΦg+RmΦm=2F2可以推出Bxq与Hxq之间的关系:Bxq=cb-1-ab-1Hxq,将该关系式画成一曲线后与衔铁的B-H曲线比较找出1个交点即为磁桥路的工作点,如图7所示.然后通过磁通连续条件Φg=Φm+Φx计算出主磁路衔铁的磁通Φx,从而得出主磁路磁感应强度Bx,查询衔铁的B-H曲线可知衔铁的工作点,得到μx1,Rx1,根据方程组(1)中的第3个方程求解出外永磁体的磁动势F1_1.通过外永磁体的磁通与通过主磁路的磁通相等,根据磁通连续原理,B1S1=BxSx1,其中,B1为对应F1的磁感应强度,S1为对应F1的径向圆周面积,Sx1为对应Rx1的衔铁径向圆周面积.外永磁体的磁动势F1_2又可以由下列关系得出:
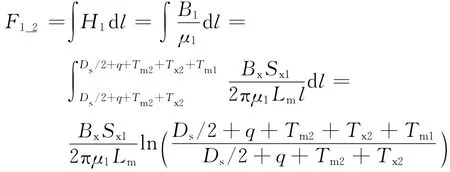
式中:H1为外永磁体的磁场强度;μ1 为外永磁体的磁导率.比较F1_1和F1_2的值,如果F1_1和F1_2相等则说明这是该励磁回路的磁化状态.将钢丝绳磁化强度Hg从小到大变化,找出一个使F1_1和F1_2的误差在允许范围内的钢丝绳磁场强度Hg和磁感应强度Bg,即为钢丝绳磁化的磁化状态.
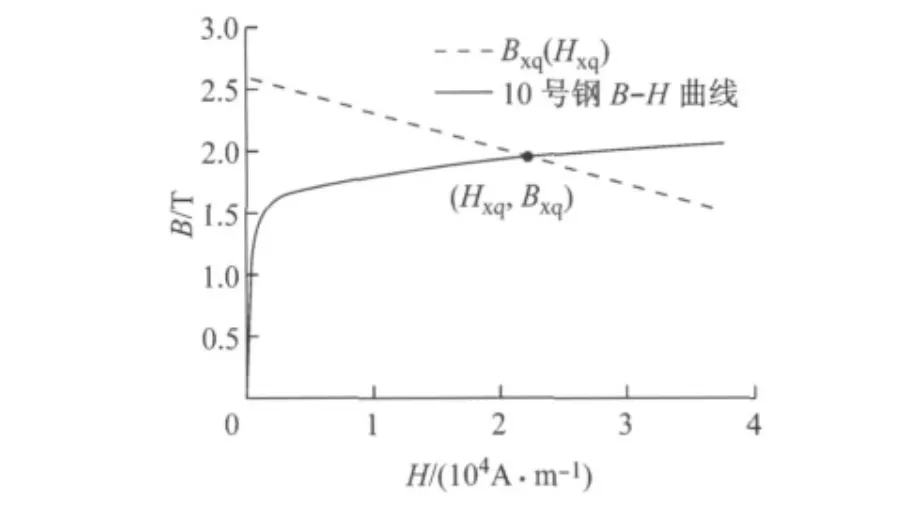
图7 磁桥路的工作点Fig.7 Operation point of magnetic bridge
3.2 励磁结构尺寸变化对励磁的影响
找出使F1_1与F1_2的误差在允许范围内的钢丝绳Hg和Bg,分析励磁结构尺寸变化后对LF检测和LMA 检测的影响,具体实现过程由MATLAB软件完成.以Lm为例,分析Lm对检测的影响.
励磁结构的尺寸取Ls=250mm,Tm1=10mm,mm,q=2mm,Lg=5mm.
3.2.1 永磁体宽度对局部缺陷型检测的影响
根据励磁结构尺寸参数设计及理论计算得出Lm变化对LF检测的影响如表1所示.Lm变大后均能提高励磁结构的磁化能力,钢丝绳的磁化磁感应强度在未饱和时随Lm的增大而大幅度增大,有利于LF的检测.
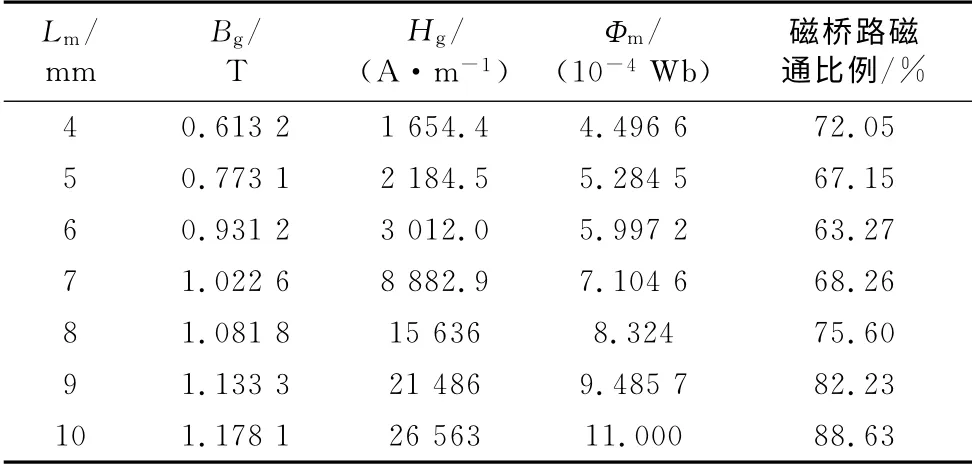
表1 永磁体宽度的变化对局部缺陷型检测的影响Tab.1 Impact of width change of permanent magnet on LF detection
3.2.2 永磁体宽度对截面积损失型检测的影响
根据励磁结构尺寸参数设计及理论计算得出Lm变化对LMA 检测的影响如表2所示.Lm的增大使桥路气隙的磁感应强度增大.在钢丝绳截面积发生变化后,桥路气隙磁感应强度也随之增大,且变化量随Lm的增大而增大,而变化率却随Lm的增大而减小.因此对LMA 检测来说,在Lm的选择上要找1个平衡点,使传感器检测的精度和灵敏度能达到综合效果较好的状态.
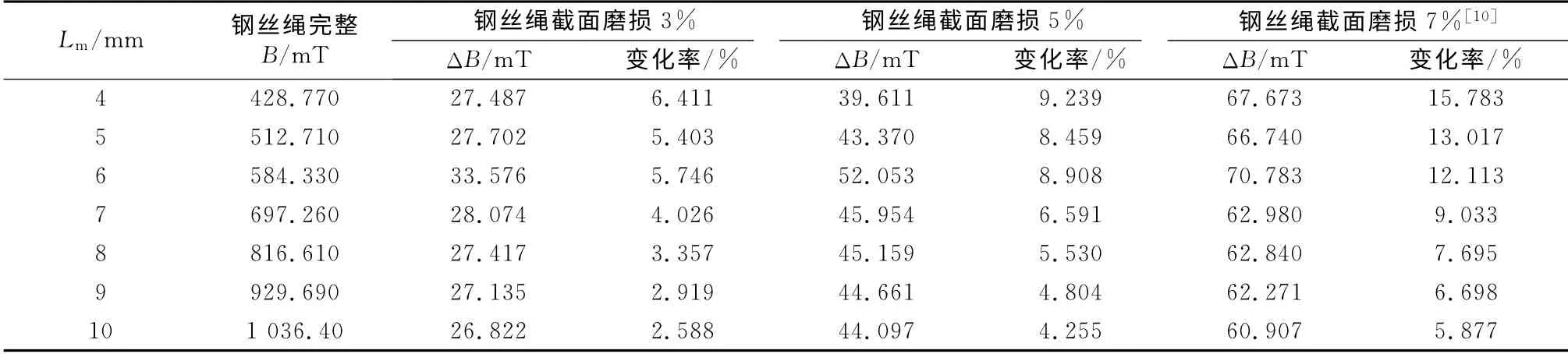
表6 优化结果Tab.6 Optimization results表2 永磁体宽度的变化对截面积损失型检测的影响Tab.2 Impact of width change of permanent magnet on LMA detection
3.3 励磁结构尺寸的确定
根据励磁结构各尺寸变化后对LF 和LMA 检测的影响和其他方面的要求,该励磁结构的尺寸选择如下:
(1)q的选择.LMA 和LF 型缺陷检测均需要一个较小的气隙q值,但是在检测中,钢丝绳相对于励磁结构是不断运动的,为了不使励磁结构与钢丝绳相互磨损,应保留一定的气隙,一般取q=2mm.
(2)Ls的选择.Ls的长度要满足能使励磁结构在钢丝绳上形成一段均匀稳定的磁化长度,使霍尔元件所处位置的励磁磁感应强度处于稳定且由外部非缺陷导致的漏磁场强度尽可能小,以利于LF漏磁通的检测.因此在励磁结构的尺寸设计中,在钢丝绳磁化段中部均匀磁场区域沿绳轴向长度应不小于钢丝绳1个股间距的长度Lmm(Lmm为钢丝绳表面相邻2股之间的距离),即Ls≥Lmm,Lmm=KDs,式中:K为钢丝绳捻距倍数,K≤6.7[7].对于典型的6X19型钢丝绳,钢丝绳的直径Ds=36 mm 时,Lmm≤241.2 mm,因此Ls≥241.2mm.根据LMA 和LF 检测对Ls的分析,Ls尽可能取小.取Ls=250.0mm.
(3)Lm,Tm1和Tm2的选择.对于剩余矫顽力较高的永磁体来说,永磁体的长度增大时磁势增加,同时内部磁阻也增大,结果在扣除永磁体内部磁势降后,对外部的磁势贡献几乎不增加,所以这类永磁体总是取扁平的形状,即磁极的面积大而厚度较小.因此在励磁回路中应尽量少用磁体串联的形式,尽量采取并联的结构形式以增大磁路的磁通量,这与上述分析的结论不冲突,因此永磁体的宽度Lm应取稍大,而Tm1,Tm2尽量取小.取Lm=7 mm,Tm1=10 mm,Tm2=10mm.
(4)Tx1的选择.不论是LMA 检测还是LF 检测,Tx1只在取值较小的一段区间内对2种检测产生较大影响.因此为了减轻装置的体积和质量,在满足衔铁不产生磁饱和的前提下,应当尽量减小衔铁厚度Tx1.取Tx1=10mm.
(5)Tx2的选择.根据Tx2尺寸的变化后对LF和LMA 检测的影响,桥路衔铁厚度Tx2取较小值,取Tx2=5mm.
(6)Lg的选择.LF 检测对Lg基本没要求,LMA 检测要求Lg尽可能取小;由于桥路气隙中还需要留出足够的空间来安装霍尔传感器,所以取Lg=5mm.
4 励磁回路ANSYS仿真
根据励磁结构尺寸的设计结果对励磁结构建立有限元分析模型,仿真励磁结构纵向截面的磁感线分布(图8).因钢棒或钢管作有限元分析与用钢丝绳作有限元分析很相似[11],考虑到ANSYS仿真的效率,以钢棒代替钢丝绳作有限元分析.根据励磁结构尺寸理论计算可知,当Lm=7 mm 时钢丝绳被检测段磁化强度达到了初度饱和区磁感应强度;但经过一系列仿真验证,在其他尺寸不变时使Lm=25 mm,钢丝绳磁化才得到了一个比较满意的结果,如图9钢丝绳被检测段磁感应强度大于1T,图9表明钢丝绳被检测段磁化强度达到了设计要求,即钢丝绳被检测段磁化强度达到了初度饱和区磁感应强度,即Lm应该取25mm 较为合适.

图8 励磁结构有限元分析模型Fig.8 Excitation structure FEA model

图9 励磁结构纵向截面的磁感线分布Fig.9 Longitudinal-sectional magnetic line distribution of excitation structure
5 结语
设计了钢丝绳无损检测励磁结构模型,从定性和定量的角度分析了钢丝绳应磁化的磁化强度,并以钢丝绳达到磁化的磁化强度作为励磁结构尺寸设计合理性的一个标准;根据等效出的励磁结构磁化回路模型,利用数值求解的方法通过变化尺寸参数得出钢丝绳磁场强度和磁感应强度,根据钢丝绳应磁化的磁化状态选择合理的理论计算尺寸;利用理论计算尺寸用ANYSYS有限元的方法仿真励磁结构的励磁回路,通过调节尺寸参数使钢丝绳磁化到需要的磁化强度,从而确定励磁结构最终尺寸,即以最终确定的尺寸参数作为励磁结构的设计尺寸.
[1] Gorbatov E K,Klekovkina N A,Saltuk V N.Steel rope with longer service life and improved quality[J].Metallurgist,2007,51(5-6):279.
[2] WANG Hongyao,HUA Gang,TIAN Jie.Research on detection device for broken wires of coal mine-hoist cable[J].Journal of China University of Mining and Technology,2007,17(3):376.
[3] Caeeiatore V, Canova A, Vallan A. Experience and technologies in NDT of ropes[J].Key Engineering Materials,2007,347:627.
[4] Phillip J,Rao C B.A new optical techniques for detection of defects in ferromagnetic material and components[J].Independent Nondestructive Testing and Evaluation International,2000.33:289.
[5] 王强.利用漏磁通法对钢丝绳进行无损探伤[J].金属制品,2005,31(6):40.WANG Qiang.Non-destructive crack detection of steel wire rope using leak magnetic flux[J].Steel Wire Products,2005,31(6):40.
[6] 王振,谭继文,胡啸奇.基于磁桥路原理钢丝绳截面积变化检测励磁器设计[J].煤矿机械,2006,27(12):16.WANG Zhen, TAN Jiwen, HU Xiaoqi. Design and application of excitation device detecting cross-sectional area of steel wire based on theory of magnetic bridge[J].Coal Mine Machinery,2006,27(12):16.
[7] 杨叔子,康宜华.钢丝绳断丝定量检测原理与技术[M].北京:国防工业出版社,1995.YANG Suzi,KANG Yihua.Quantitative inspection for broken wires of wire ropes principle and technique [M].Beijing:National Defence Industry Press,1995.
[8] 林其壬,赵佑民.磁路设计原理[M].北京:机械工业出版社,1987.LIN Qiren,ZHAO Youmin.Magnetic circuit design principles[M].Beijing:Chine Machine Press,1987.
[9] 邹继斌,刘宝廷,崔淑梅,等.磁路与磁场[M].哈尔滨:哈尔滨工业大学出版社,1998.ZOU Jibin,LIU Baoting,CUI Shumei,et al.Magnetic circuit and magnetic field [M]. Harbin: Harbin Institute of Technology Press,1998.
[10] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 5972—2009/ISO 4309:2004起重机钢丝绳保养、维护、安装、检验和报废[S].北京:中国标准出版社,2010.General Administration of Quality Supervision,Inspection and Quarantine of the P R China,Standardization Administration of P R China.GB/T 5972—2009/ISO 4309:2004Cranes-wire ropes-care, maintenance, installation, examination and discard[S].Beijing:China Standard Press,2010.
[11] 曹印妮.基于漏磁成像原理的钢丝绳局部缺陷定量检测技术研究[D].哈尔滨:哈尔滨工业大学,2007.CAO Yinni.Study on wire rope local flaw quantitative testing based on MFL imaging principle[D]. Harbin: Harbin Institute of Technology Press,2007.
