混凝土中毛细压力-饱和度关系模型

张庆章，顾祥林，张伟平，黄庆华

（同济大学 建筑工程系，上海 200092）

混凝土结构耐久性研究中往往需要准确地确定混凝土中水分含量和水分传输过程.海洋环境下飞溅区、潮汐区混凝土孔隙中水分不但是氯离子扩散的介质，还是携带氯离子移动的载体.由于干湿交替的影响，浅层混凝土内水分传输速率很大，在氯离子传输过程中起到主要作用，而混凝土吸湿和排湿过程中毛细压力和饱和度之间关系恰恰是研究混凝土内水分传输的关键因素［1-2］.

研究证明，达西定律可以推广到非饱和混凝土内水分的传输中［3］.达西定律中的渗透系数为常数，而非饱和混凝土中水分传输系数是混凝土饱和度的函数.根据质量守恒定律，水流入混凝土内的质量与流出质量相等.不考虑孔隙内液态水转化为水蒸气部分，水分的传输方程可表示为［4］

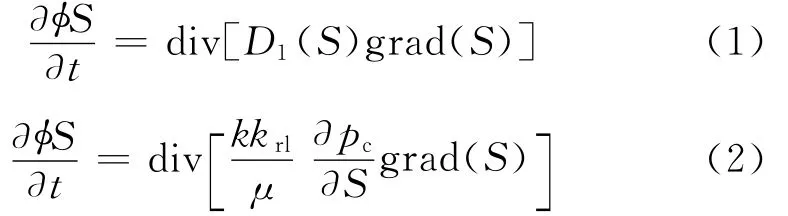
式中：φ为混凝土的孔隙率；S为饱和度即液态水占据孔隙体积的比值；D1（S）为液态水传输系数，m2·s-1；t为时间，s；k为混凝土固有渗透率，m2；krl为液态水相对渗透率；pc为毛细压力，Pa；μ为水的动力粘度系数，Pa·s.从式（2）可以看出毛细压力与饱和度之间的关系是研究非饱和混凝土中水分传输的基本条件.

文献［5］通过研究不同外部压力作用下土壤中水分达到平衡状态时土壤中的饱和度建立了两者之间的关系.文献［6-7］在文献［5］研究基础上分别进行了不同水灰比混凝土在不同相对湿度下的排湿试验，证实了通过土壤这种多孔介质建立的排湿关系对于混凝土材料也有很好的适用性.Ishida等［8］试图建立不同温度下吸湿和排湿过程中相对湿度与饱和度之间关系，为此进行了水灰比为0.5的水泥浆在20，40，60℃下吸湿和排湿研究，结果表明温度对吸湿过程的影响不大，而对排湿过程有较大影响.随着温度的升高，相同相对湿度下失去的水分增多.Xi等［9］通过分析水泥材料吸湿试验结果建立了吸湿过程中考虑水泥的类型、养护的龄期、温度等因素影响的水分含量与相对湿度之间的关系.

虽然通过试验可以测量吸湿和排湿过程中毛细压力和饱和度之间的关系，但是试验繁琐、试验周期很长，而且混凝土配合比稍有变化都必须进行重复试验，给水分传输理论的研究和应用带来较大困难［10-11］.因此，本文从混凝土孔隙中液态水和气相各自内部压力在接触面上存在着不连续性而产生的毛细压力为出发点利用Young-Laplace方程和Kelvin方程建立混凝土内液态水和水蒸气的平衡关系，分析排湿过程同一相对湿度对应饱和度比吸湿过程高的原因，然后结合文献［9］中吸湿过程毛细压力与饱和度关系建立混凝土排湿过程中毛细压力与饱和度之间非线性关系方程，在此基础上引入等比容吸附热量的影响建立在不同温度条件下混凝土中毛细压力与饱和度关系模型.

1 混凝土孔隙水分平衡关系

1.1 毛细压力与孔隙半径的关系

在非饱和混凝土中，液态水和气相各自内部压力在接触面上存在着不连续性，将产生毛细压力，使液态水驱使气相向混凝土内部流动.毛细压力是水分在非饱和混凝土内传输的重要的驱动力.非饱和混凝土中毛细压力pc为液态水内部压力p1与外部气相（包括水蒸气和其他气体）压力pa之差.

该压力差的大小取决于液态水弯液面的曲率和界面的张力，如图1所示，图中φ1，φ2分别为界面正交方向上2个弧中心角；γ1，γ2为界面正交方向上2个曲率半径，m；σ为水分表面张力，N·m-1；s，l分别为相互正交的弧长，m.根据平衡关系可得到Young-Laplace方程［12］

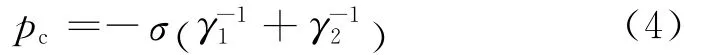
一般假设弯液面为球形曲面，孔隙半径r与弯曲液面曲率半径γ以及接触角φ之间的关系如图2所示.由于混凝土孔隙的表面比较粗糙，可以认为cosφ＝1，因此式（4）可变为

从Young-Laplace方程可以知道混凝土孔隙内液态水的弯曲曲率导致液态水表面内外的压力不同.对于凹液面，液面下的压力比液态水外即气相的压力小，产生毛细压力的负压；对于凸液面，液面下的压力比液体外气相压力大，产生毛细压力的正压.

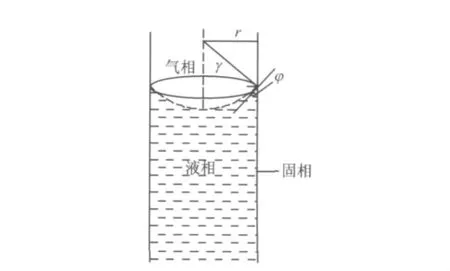
图2 接触角不为零时弯液面Fig.2 Bended liquid surface when contact angle is not zero

1.2 液态水和水蒸气转化过程

混凝土孔隙中液态水和水蒸气在孔隙中的传输也伴随着液态水和水蒸气相互转化的过程.在相对湿度较低时，一定温度下，由于液体分子的热运动，一些液体分子从液态水表面逃逸出形成水蒸气，随着水蒸气分子的增多，水蒸气的密度增加，产生的压力也增加，压力最终稳定在固定的数值，即饱和蒸汽压.这时液态水的水分子不断地汽化，水蒸气的水分子也在不停地液化，并且汽化速率和液化速率相同，液态水和水蒸气达到了平衡状态.当相对湿度较高时，水蒸气液化的速率大于液态水汽化的速率，相对湿度降低，最终达到液态水和水蒸气相互转化的平衡状态［13］.

根据热力学平衡理论，可得Gibbs-Duhem方程［14］

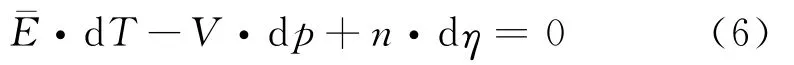
如果水蒸气和液态水处于热力学平衡状态，则

式中：ηv为水蒸气分子的化学势能，J·mol-1；ηl为液态水分子的化学势能，J·mol-1.根据文献［14］可以建立相对湿度h与毛细压力关系，即

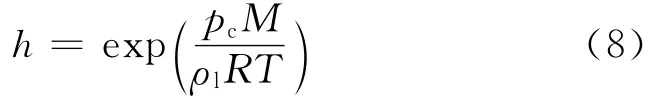
式中：M 为水的摩尔质量，0.018kg·mol-1；ρl为水的密度，kg·m-3；R 为气体常数，R＝8.314J·mol-1·K-1.将式（5）代入式（8）可得

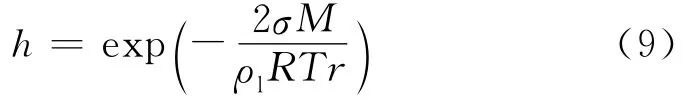
式（9）即为Kelvin方程，从式（9）可以发现混凝土孔隙中的相对湿度与孔隙半径直接相关.对于某孔半径为r时，处于平衡状态下的相对湿度值为hr，如果相对湿度值超过hr孔隙中的水蒸气将发生液化，转化成液态水.

假设混凝土处于25℃的环境下，则水的表面张力σ＝0.073N·m-1，密度ρl＝1000kg·m-3［14］，根据式（9）得

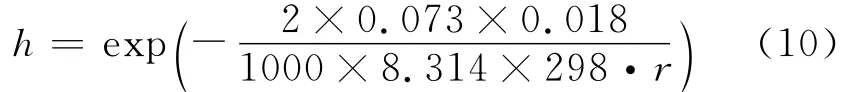
对式（10）求解可以发现，孔隙半径r＝1nm时，h＝0.35；r＝2nm 时，h＝0.59；r＝50nm 时，h＝0.98.据此可知，毛细液化基本上从1nm或者2nm开始而终止于50nm左右.孔隙半径越小，平衡时的相对湿度h也越小.根据式（8）中毛细压力与相对湿度之间关系可知相对湿度越小毛细压力数值越大.那么随着孔隙半径的减小，水分越容易沿着孔隙进入混凝土内部.

2 吸湿过程中毛细压力与饱和度关系

在干湿交替环境下的混凝土结构干燥时水分向外传输，并向外部蒸发，当湿润时，水分又向混凝土内传输.当水分向混凝土内部传输时，混凝土吸湿曲线起了很重要的作用.混凝土水分吸湿曲线是指混凝土吸收水分时相对湿度与混凝土内饱和度的平衡关系曲线.与此相似，干燥过程时相对湿度与混凝土内饱和度的平衡关系曲线为排湿曲线.

对于干湿交替区域混凝土直接吸入的过程，内部相对湿度与饱和度的平衡关系很难测定.一般混凝土直接吸水时通过吸湿曲线间接确定这种平衡关系.但是这种方法试验周期很长也很繁琐，给应用带来不便.为此，Xi等［9］通过大量试验数据的分析建立了较为通用的三参数水泥材料内含水质量分数与相对湿度关系方程，如式（11）所示.该方程在相对湿度5%～100%范围内均适用.

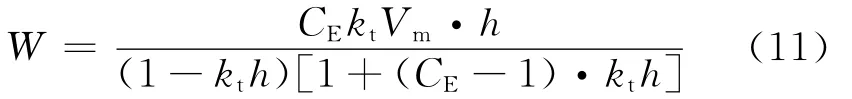
式中：W 为相对于水泥浆的含水质量分数，kg·kg-1；CE为能量参数；kt为常数，kt∈（0，1）；Vm为单位水泥浆质量吸附水分子单层质量，kg·kg-1.

各种因素对吸附单层水分子的质量Vm的影响关系可以表示为

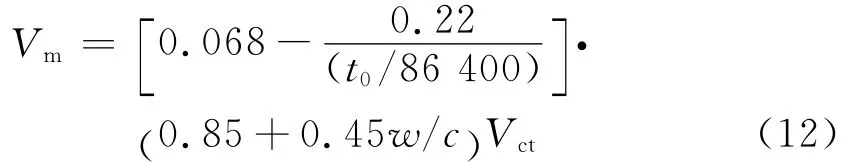
式中：t0为养护时间，s，当t0≤432000s（即t0≤5d）时，取t0＝432000s；w，c分别为水和水泥的质量，当w／c＜0.3时，取w／c＝0.3，当w／c＞0.7时，取w／c＝0.7；Vct为水泥类型影响系数，当水泥为类型Ⅰ时，Vct＝0.9，类型Ⅱ时，Vct＝1，类型Ⅲ时，Vct＝0.85，类型Ⅳ时，Vct＝0.6.根据 ASTMC-150，一般波特兰水泥为类型Ⅰ，抗硫酸盐且产生中等水化热水泥为类型Ⅱ，早强水泥为类型Ⅲ，低热水泥为类型Ⅳ［15］.

温度T对能量参数CE的影响关系为

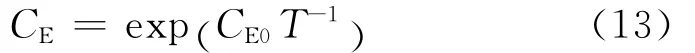
式中，CE0为常数，CE0＝855.

各种因素对参数kt的影响关系可以表示为

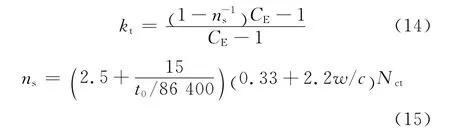
式中：Nct为水泥类型影响系数.当水泥为类型Ⅰ时，Nct＝1.10，类型Ⅱ时，Nct＝1.00，类型Ⅲ时，Nct＝1.15，类型Ⅳ时，Nct＝1.50.

如果忽略混凝土中骨料和界面过渡区对混凝土内饱和度的影响，式（11）对混凝土而言是适用的.由式（11）解出h，即

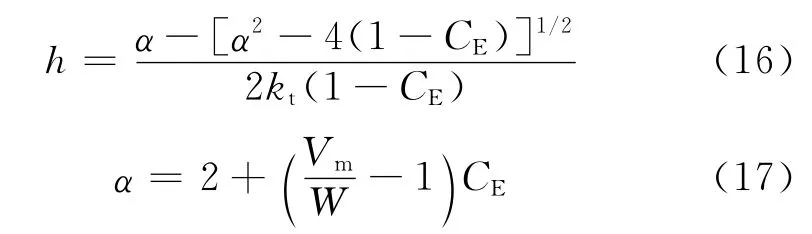
式（8）和式（16）联立可得到毛细压力与孔隙水含量之间的关系，即

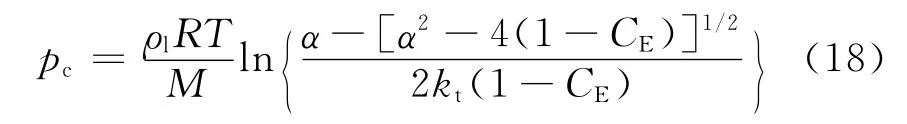
对于水泥类型为Ⅰ型、w／c＝0.53、养护龄期为28d的普通硅酸盐混凝土根据式（16）可以得到吸湿过程不同温度时含水质量分数与相对湿度的关系，如图3.

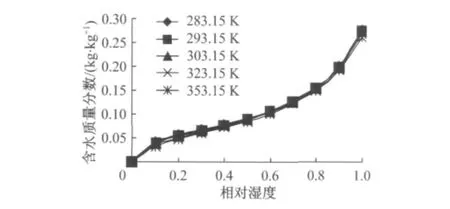
图3 吸湿过程不同温度时含水质量分数与相对湿度的关系Fig.3 Relationship between mass fraction of water and relative humidity in absorption process at different temperatures

从图3可以看出，吸湿过程温度对含水质量分数的影响很小.因此假设20℃相对湿度为100%时混凝土中含水达到饱和状态，即式（17）可以变化为

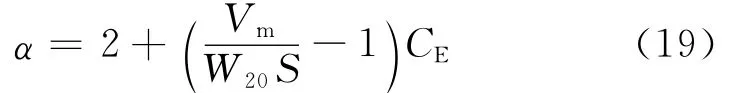
式中：W20为20℃混凝土饱和时相对于水泥浆的含水质量分数，kg·kg-1.

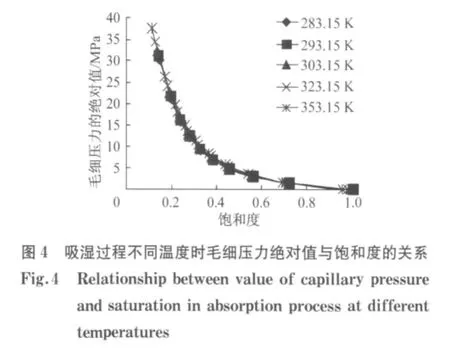
将式（19）代入式（18）即可建立混凝土内毛细压力与饱和度之间的关系.对于水泥类型为Ⅰ型，w／c＝0.53，养护龄期为28d的普通硅酸盐混凝土（w20＝0.274）（图3）的毛细压力绝对值与混凝土饱和度之间的变化关系如图4.可见温度在混凝土吸湿过程中影响非常小，可以忽略不计.

3 排湿过程中毛细压力与饱和度关系

3.1 排湿比吸湿滞后原因分析

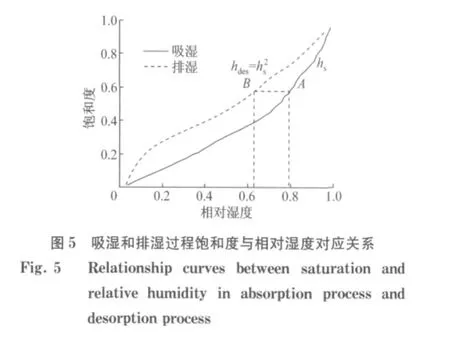
大量试验都表明排湿过程同一相对湿度对应饱和度比吸湿过程时高，这种现象称为滞后效应，如图5所示［4，16］，图中，hs为吸湿过程时相对湿度；hdes为排湿过程时相对湿度.滞后效应的形成主要由于吸湿和排湿弯液面的不同而引起.

假设混凝土的孔隙由一系列两端开放的圆柱孔组成，并且各圆柱孔之间的孔径分布连续.吸湿过程中当相对湿度为hs时，较小的孔隙内水蒸气转化液态水并逐渐被充满.孔隙1吸附水厚度达到吸湿时吸附水的厚度ts时即达到产生液化水的平衡状态，此时孔隙中水分的液面曲率半径如图6a所示，图中，r1，r2分别为孔隙半径.当相对湿度降低时，孔隙中吸附水的厚度减小.排湿过程中当相对湿度达到hdes时开始排湿，孔隙2中达到气液的平衡状态，开始发生排湿过程，此时孔隙中水分的液面曲率半径如图6b所示，图中，td为排湿时吸附水的厚度，m.结合式（4）和式（8）以及图6中的曲率半径关系，吸湿和排湿过程中吸附水厚度与相对湿度的平衡关系为［17］

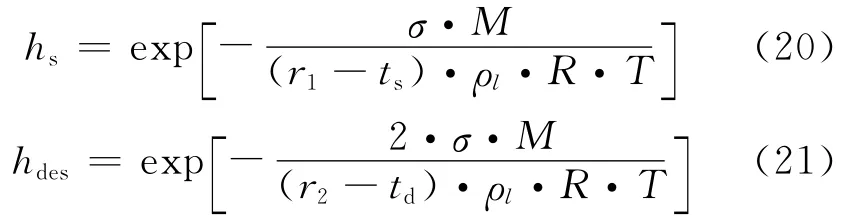
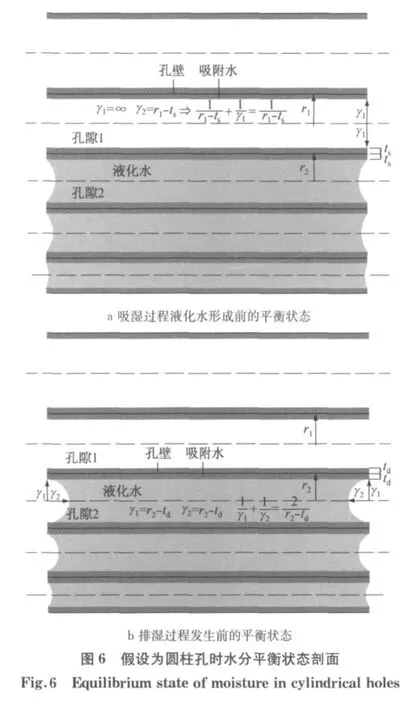
一般吸附水质量相对总含水质量是很小的，因此忽略吸湿和排湿过程中因吸附水厚度的不同引起的含水质量分数变化.由于孔径分布连续，可以认为r1与r2相等.那么混凝土中含水质量分数相同时吸湿和排湿过程的相对湿度关系为［18］

以吸湿曲线预测排湿曲线如图5所示.吸湿曲线A点对应相对湿度hs与混凝土内饱和度平衡状态，以A点开始逐渐降低相对湿度，开始阶段水分质量保持不变，直到相对湿度达到hdes即时，水分才开始减少.

3.2 毛细压力与饱和度关系模型

根据排湿相对于吸湿饱和度滞后原因分析，如果把混凝土孔隙假设为圆柱形孔，联立式（16）、式（22）得排湿过程相对湿度与饱和度之间关系，即

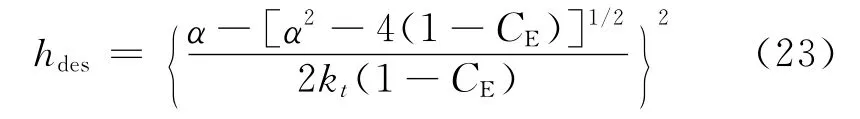
于是有

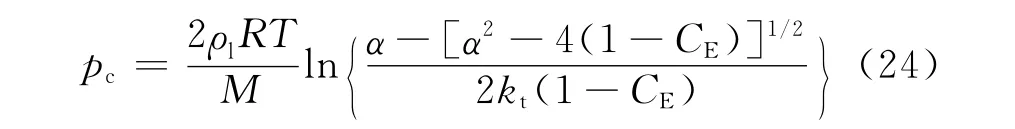
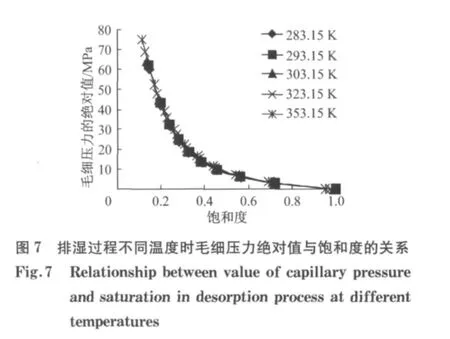
对于水泥类型为Ⅰ型、w／c＝0.53、养护龄期为28d的普通硅酸盐混凝土，根据式（24）可以得到排湿过程中毛细压力绝对值与饱和度之间的关系如图7所示.可以看出该模型无法体现温度的影响.根据Poyet等［19］进行的30℃和80℃下混凝土水分排湿试验研究（图8）可以看出随着温度的升高同样相对湿度对应的饱和度明显降低.Ishida等［8］进行了不同温度下水泥浆水分排湿试验研究，也得出相似的变化规律.因此，建立排湿曲线时必须考虑温度的影响.

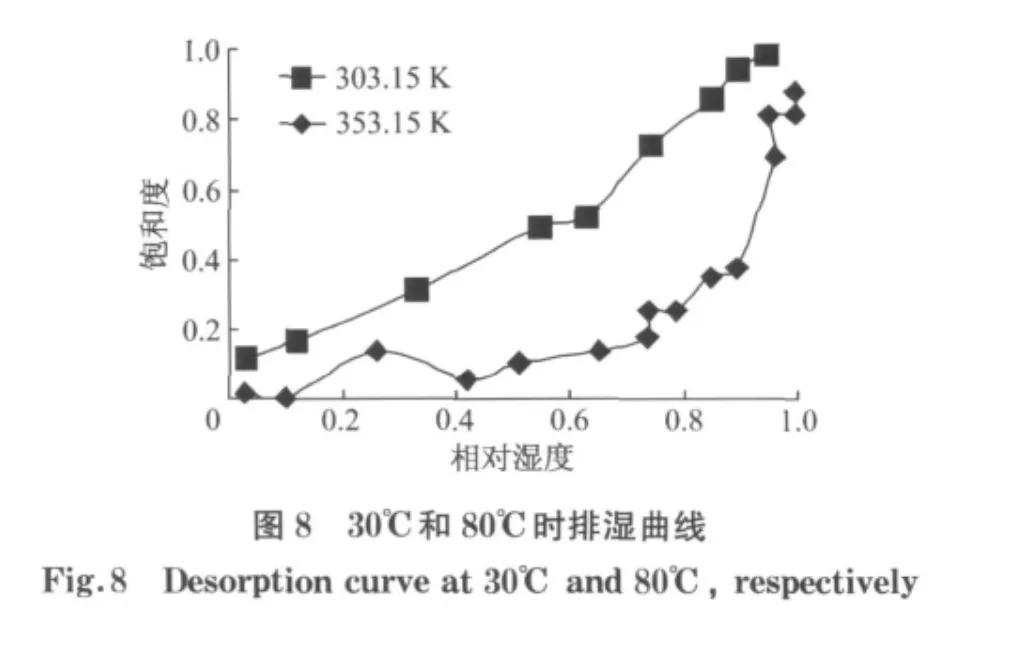
3.3 考虑温度修正的毛细压力与饱和度关系模型

温度对排湿曲线的影响主要因为等比容吸附热量引起的，可以用Clausius-Clapeyron方程表示［19-20］，即

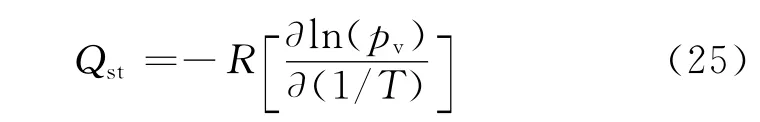
式中：Qst为等比容吸附热量，J·mol-1.对式（25）变换得

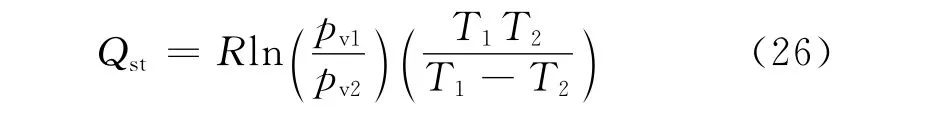
式中：pv1，pv2分别为绝对温度为T1，T2时水蒸气压力，Pa.即

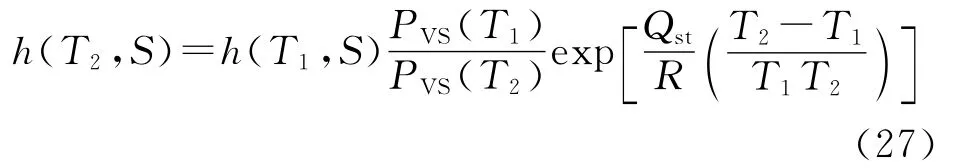
式中：h（T1，S），h（T2，S）分别为 T1，T2时、饱和度为S时相对湿度；PVS（T1），PVS（T2）分别为 T1，T2时饱和蒸汽压，Pa.

根据Poyet试验结果，Qst随S的变化关系如图9.根据图9试验结果可以回归出Qst与S的关系为

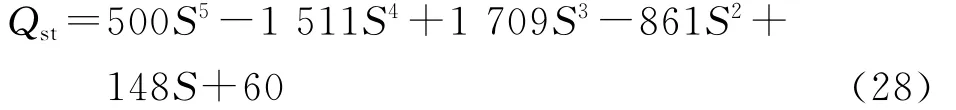
图9 等比容热量随饱和度变化关系Fig.9 Relationship between isosteric heat and saturation

以T1＝293.15K时的排湿曲线作为参考标准，式（8）代入式（27）左侧项、式（23）代入右侧h（T1，S），经整理得不同温度时毛细压力与饱和度关系为

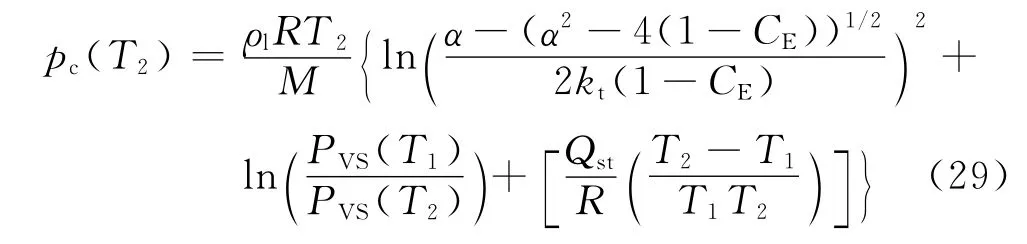
饱和蒸汽压力PV，S随温度变化关系可表示为［21］

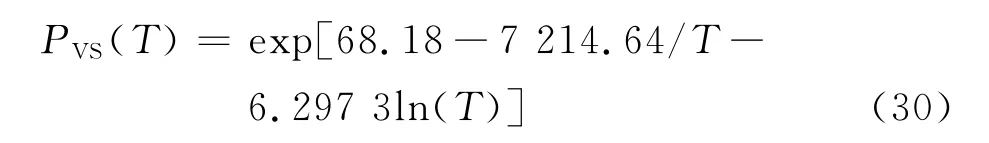
以20℃时的排湿曲线作为参考标准，结合式（27）、式（30）得到不同温度下的排湿曲线，与文献［19］中30℃和80℃时w／c＝0.43的混凝土试验结果的对比如图10所示，可以发现随着温度的升高相同相对湿度对应的饱和度逐渐减小.理论模型在30℃附近时可以大致模拟这种变化关系，而到80℃时模拟结果与试验结果相差较大.目前关于温度对相对湿度、毛细压力与饱和度之间关系的影响规律研究成果较少，通用模型还没有建立，即使常温下相对湿度、毛细压力与饱和度之间关系往往也是通过试验方式确定的.因此，在没有试验数据的情况下，可分别利用式（27）和式（29）粗略预测不同温度下相对湿度、毛细压力与饱和度之间的关系.

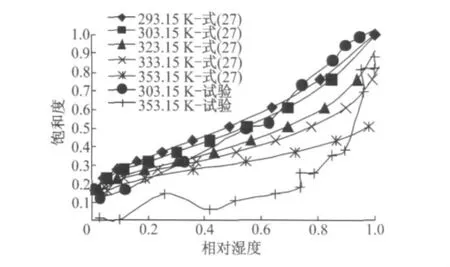
图10 不同温度下计算排湿曲线与试验数据对比Fig.10 Comparison between computed desorption curves and test curves at different temperatures

对于水泥类型为Ⅰ型、w／c＝0.53、养护龄期为28d的普通硅酸盐混凝土，考虑温度修正后排湿过程中毛细压力与饱和度之间的关系如图11所示.与图7对比可以看出，考虑等比容吸附热量修正后，在排湿过程中毛细压力与饱和度之间关系随温度的变化已经体现出来，同样大小的饱和度对应的毛细压力数值随着温度的升高逐渐降低.

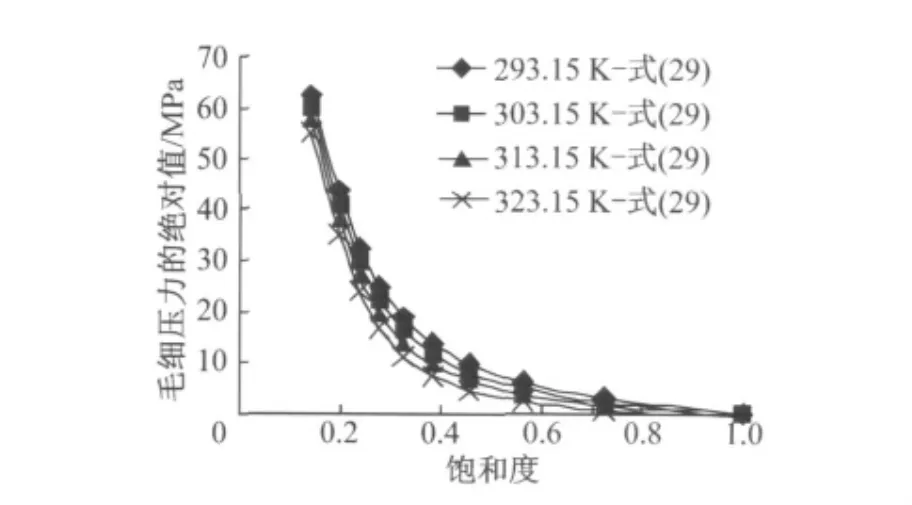
图11 不同温度下毛细压力绝对值随饱和度变化Fig.11 Relationship between absolute value of capillary pressure and saturation at different temperatures

4 结语

混凝土孔隙中液态水和气相界面处存在一个弯液面，弯液面两侧的压力是不连续的，导致毛细压力产生，并驱动水分传输.

混凝土中孔隙半径越小，平衡相对湿度也越小，毛细压力数值越大，水分越容易进入混凝土内部.

根据排湿过程相对于吸湿过程滞后原因分析并结合现有吸湿模型提出了排湿过程中毛细压力与饱和度的关系模型.

通过引入等比容吸附热量的影响分析了不同温度条件下毛细压力与饱和度之间的相关关系，发现随着温度的升高同样饱和度对应的毛细压力数值减小.

本文建立的考虑温度修正后的相对湿度、毛细压力与饱和度关系模型在温度较高时误差较大，给应用带来一定的限制，有待进一步研究.

［1］Ababneh A，Benboudjema F，Xi Y P.Chloride penetration in nonsaturated concrete［J］.Journal of Materials in Civil Engineering，2003，15（2）：183.

［2］Iqbal P O N，Ishida T.Modeling of chloride transport coupled with enhanced moisture conductivity in concrete exposed to marine environment［J］.Cement and Concrete Research，2009，39（4）：329.

［3］仵彦卿.多孔介质污染物迁移动力学［M］.上海：上海交通大学出版社，2007.WU Yanqing.Pollutant migration dynamics in porous media［M］.Shanghai：Shanghai Jiaotong University Press，2007.

［4］Baroghel-Bouny V.Water vapour sorption experiments on hardened cementitious materials part II：essential tool for assessment of transport properties and for durability prediction［J］.Cement and Concrete Research，2007，37（3）：438.

［5］Van Genuchten M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils［J］.Soil Science Society of America Journal，1980，44（5）：892.

［6］Savage B M，Janssen D J.Soil physics principles validated for use in predicting unsaturated moisture movement in portland cement concrete［J］.ACI Materials Journal，1997，94（1）：63.

［7］Baroghel-Bouny V， Mainguy M，Lassabatere T，et al.Characterization and identification of equilibrium and transfer moisture properties for ordinary and high-performance cementitious materials［J］.Cement and Concrete Research，1999，29（8）：1225.

［8］Ishida T，Maekawa K，Kishi T.Enhanced modeling of moisture equilibrium and transport in cementitious materials under arbitrary temperature and relative humidity history［J］，Cement and Concrete Research，2007，37（4）：565.

［9］Xi Y P，Bažant Z P，Jennings H M.Moisture diffusion in cementitious materials adsorption isotherms［J］.Advanced Cement Based Materials，1994，1（6）：248.

［10］Baroghel-Bouny V. Water vapour sorption experiments on hardened cementitious materials part I：essential tool for analysis of hygral behaviour and its relation to pore structure［J］.Cement and Concrete Research，2007，37（3）：414.

［11］Akita H，Fujiwara T，Ozaka Y.A practical procedure for the analysis of moisture transfer within concrete due to drying［J］.Magazine of Concrete Research，1997，49（179）：129.

［12］姚海林.关于基质吸力及几个相关问题的一些思考［J］.岩土力学，2005，26（1）：67.YAO Hailin.Some considerations about the concept of matric suction and questions related to matric suction［J］.Rock and Soil Mechanics，2005，26（1）：67.

［13］高世桥.毛细力学［M］.北京：科学出版社，2010.GAO Shiqiao.Capillary mechanics［M］.Beijing：Science Press，2010.

［14］Černy R，Rovnaníková P.Transport processes in concrete［M］.London：Spon Press，2002.

［15］Ramachandran V S. Concrete admixtures handbook—properties，science，and technology［M］.Park Ridge：Noyes Publications，1984.

［16］Maekawa K，Chaube R，Kushi T.Modelling of concrete performance：hydration，microstructure formation and mass transport［M］.London：Taylor ＆Franci，1999.

［17］Espinosa R M，Franke L.Influence of the age and drying process on pore structure and sorption isotherms of hardened cement paste［J］.Cement and Concrete Research，2006，36（10）：1969.

［18］Espinosa R M，Franke L.Inkbottle pore-method：prediction of hygroscopic water content in hardened cement paste at variable climatic conditions［J］. Cement and Concrete Research，2006，36（10）：1954.

［19］Poyet S，Charles S.Temperature dependence of the sorption isotherms of cement-based materials：heat of sorption and Clausius-Clapeyron formula ［J］. Cement and Concrete Research，2009，39（11）：1060.

［20］Brunauer S.The adsorption of gases and vapors ［M］.Princeton：Princeton University Press，1945.

［21］Mainguy M. Modeling of moisture transfer isotherms of porous media：application to the drying of cement-based materials［D］.Paris：Ecole Nationale des Ponts et Chaussées，1999.