回风巷断面突然变化段粉尘运动规律及浓度分布的数值模拟＊

莫 樊 郁钟铭 吴桂义

（1.贵州民族学院建筑工程学院，贵州省贵阳市，550025；2.贵州大学矿业学院，贵州省贵阳市，550003）

回风巷断面突然变化段粉尘运动规律及浓度分布的数值模拟＊

莫 樊1郁钟铭1吴桂义2

（1.贵州民族学院建筑工程学院，贵州省贵阳市，550025；2.贵州大学矿业学院，贵州省贵阳市，550003）

根据气固两相流理论，探索性地提出了利用回风巷断面突然变化降尘方法，采用计算流体力学的离散相模型对回风巷断面突然扩大粉尘浓度分布进行数值模拟，总结出回风巷断面突然变化段粉尘浓度沿程分布及变化规律。

矿井防尘 气固两相流 流体力学 断面突变

1 概述

通过对贵州省六盘水矿区煤矿进行资料的收集及现场调研发现，风流净化水幕湿式除尘是综采工作面回风巷最普遍的降尘方式，劳动强度虽然不大，但需要专人负责，造成了许多不便。而目前采取的降尘方法是仅在回风巷中安设两道水幕，甚至有时由上班工人观察粉尘量来控制洒水降尘。虽然也有一些矿井采用了自动控制方式，但存在一定弊端，降尘效果也较差，不能解决粉尘污染的实际问题。其喷雾压力、喷头组数的选择基本也仅是依靠经验值进行设置。贵州省内部分煤矿，底板存在粉砂质泥岩、泥岩、炭质泥岩、煤等软弱岩层，力学强度很低，在底板遇水后有膨胀的现象，对巷道支护及工作面的推进极其不利，且煤层孔隙率低，不易注水，故大部分煤矿对于煤层注水和喷雾降尘方法的使用非常慎重。因此研究利用回风巷断面突然变化的方法对巷道粉尘进行自然沉降具有重要的意义。

针对贵州地质特殊的煤矿的防尘效果，笔者对六盘水矿区响水煤矿的W134综采工作面进行粉尘浓度的现场实测，并探索性地提出了利用回风巷断面突然变化降尘方法，对回风巷粉尘浓度分布进行数值模拟，根据实测数据和计算结果提出综采工作面回风巷粉尘防治方法。

2 气固两相流模型

研究粉尘在回风巷的运动离不开采面巷道里空气的流动，粉尘在气流中的运动属于气固两相流的范畴，故而建立粉尘移运规律（浓度分布和运动规律）的数学模型，实质上就是建立气固两相流动的数学模型。

2.1 气体流动的数学模型

气体流动数学模型主要用来确定工作面气体的速度场和压力分布。其中对回风巷中的气体流动控制方程组采用三维稳态不可压N－S方程，湍流模型采用k－ε双方程模型，是目前应用最广泛的工程湍流模型，模型内只考虑动量传输，忽略传热。具体形式如下：

连续方程：

运动方程：

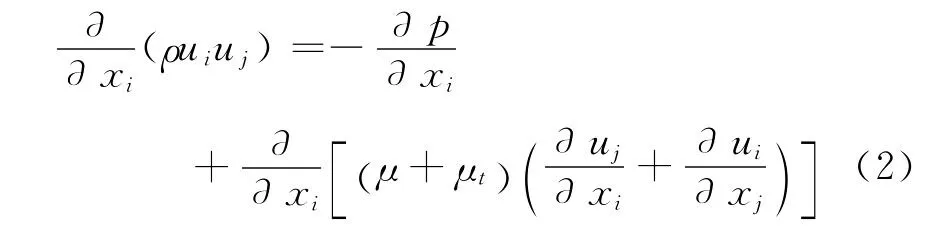
k方程：

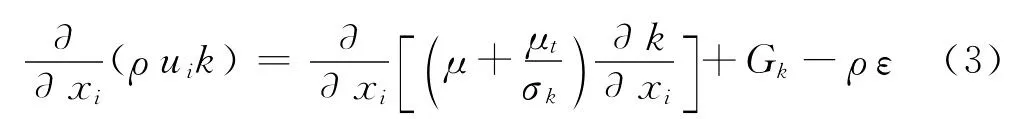
ε方程：

式中：Gk——剪切力变化产生的湍动能变化率；

k——湍动能，m2／s2；

ε——湍动能耗散率，m2／s3；

μ——层流粘性系数，Pa·s；

μt——湍流粘性系数，Pa·s；

p——湍流有效压力，Pa；

ρ——气体密度，kg／m3；

xi——x、y、z方向上的坐标，m；

ui——x、y、z方向上的速度，m／s。

Cε1、Cε2、Cμ、σε和σk——常数，分别取1.441.920.091.3和1.0

2.2 离散相的数学模型

由于模拟粉尘在巷道断面变化处的扩散，回风巷粉尘的浓度不超过12%，局部浓度也不会大于12%，其对连续相的作用可以忽略不计，因此本文拟采用欧拉－拉格朗日中的离散相模型（DPM），即用欧拉观点描述气相流场，而用拉格朗日观点描述颗粒的运动。离散相模型采用球形颗粒（回风巷中的粉尘颗粒）构成的第二相分布在连续相（风流）中，并且应用随机方法来考虑瞬时湍流速度对颗粒轨道的影响，从而模拟计算粉尘颗粒的运移规律轨迹，以及浓度分布。

DPM模型通过积分拉格朗日坐标下颗粒作用力的微分方程来求解颗粒的轨道，颗粒相的作用力

平衡方程为：

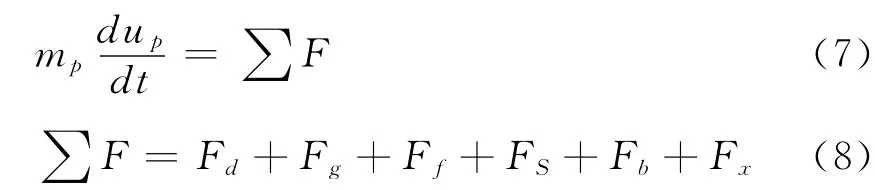
式中：mp——颗粒质量，mg；

up——颗粒运动速度；m／s；

∑F——颗粒所受合力，N；

Fd——颗粒运动所受阻力，N；Fg——颗粒所受重力，N；Ff——颗粒所受浮力，N；

Fx——颗粒所受其它作用力，包括附加质量力，旋转时的马格卢斯（Magnus）升力，热泳力，萨弗曼（Saffman）升力，布朗力等等。其中附加质量力，马格卢斯（Magnus）升力，热泳力等作用力的数量级都很小，文中忽略不计。

3 回风巷几何模型的建立及边界条件的设定

3.1 几何模型的建立

为了更全面地得到粉尘在回风巷的扩散规律，根据六盘水矿区响水煤矿W134综采工作面及回风巷具体情况及相关实测数据，建立由一个断面变化前长为20m、宽4.4m、高3m的长方体巷道、一个长10m、宽8.4m、高3m的断面变化区域和一个断面变化后长为10m、宽4.4m、高3m的长方体巷道3部分组成的计算区域。简化后使用GAMBIT2.0建立三维几何模型，并划分计算网格。其三视图的局部放大见图1、图2。

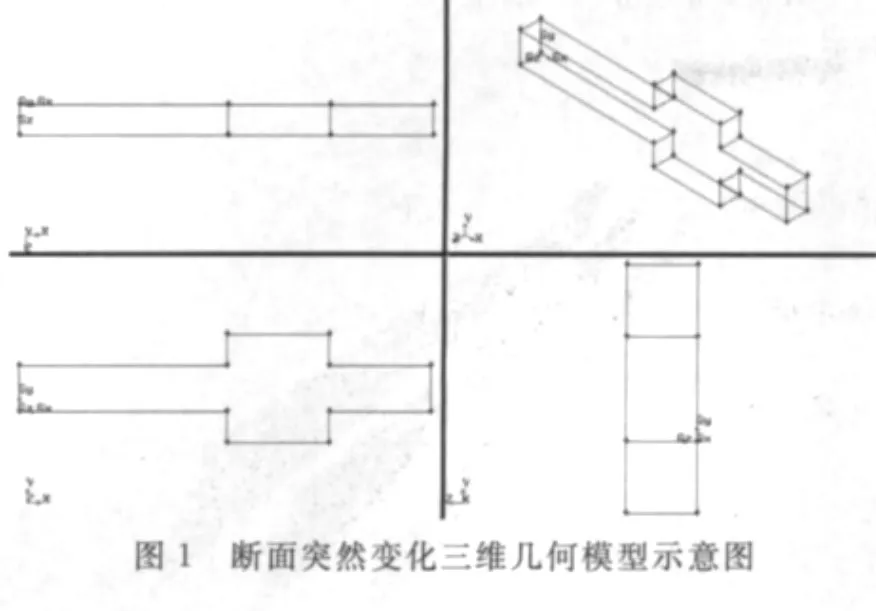
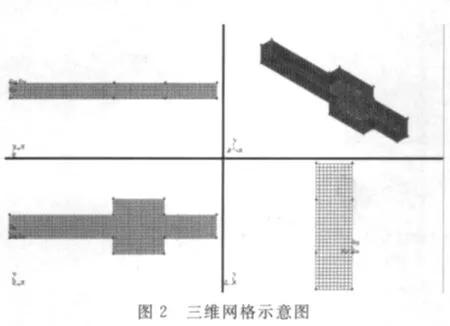
3.2 边界条件的设定

将GAMBIT2.0建立的三维几何模型导入FLUENT6.2中，结合数学模型和FLUENT的模拟方法，确定数值模拟的各参数及边界条件如下：巷道过流断面面积为10.5m2，流体与固体基础周长14.8m，入口风速3.3m／s，水力直径3.57m，粒径分布，罗辛－拉穆勒（Rosin－Rammler）分布，粉尘浓度16.8×10－6kg／m3（由于用FLUENT 6.2解算得到的粉尘浓度单位为kg／m3，所以本文中粉尘浓度的单位统一使用kg／m3，质量流率0.00058212kg／s，喷射源类型面喷射，湍流扩散模型为随机轨道模型。

其中，湍流强度由公式（9）确定：

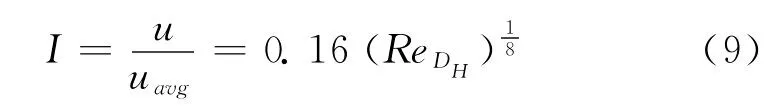
式中：u、uavg——湍流脉动速度与平均速度，m／s；

ReDH——按水力直径计算的雷诺数水力直径由公式（10）确定：

式中：A——过流断面面积，m2；

S——流体与固体基础周长，m。

入口速度与实际回风巷风速相等，即入口风速应为3.3m／s。

质量流率按照公式（11）计算：

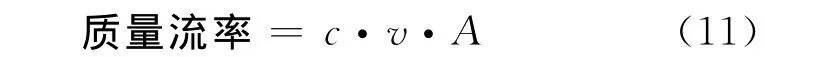
式中：c——尘源处粉尘浓度，实测数据，取16.8×10－6kg／m3；

v——巷道内的风速，取3.3m／s；

A——巷道断面积，10.5m2。

各参数如上所示，同时考虑到进风巷的粉尘浓度，各参数参照相关的实测数据设置，文中不做详细说明。

4 数值模拟结果与分析

按照以上参数设置，通过FLUENT6.2解算后，经过提高计算精度，区域网格自适应等调试改进后，将得到的计算结果做分析。

4.1 回风巷断面突然变化模型风流流场的运动规律

用FLUENT6.2进行解算，模拟回风巷断面突然变化巷道的风流流场，根据模拟风流流场的结构特点，巷道风流出现了3个区域：层流区、湍流区和涡流区。

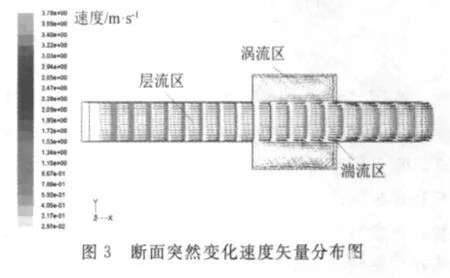
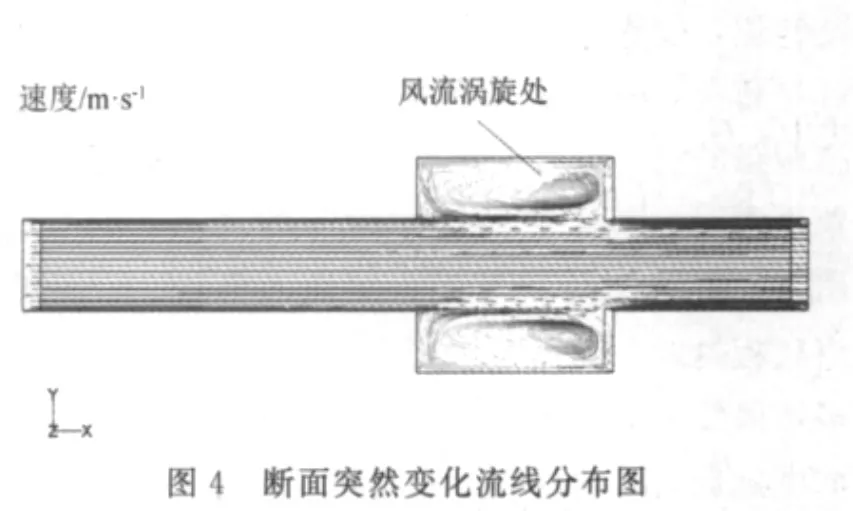
断面突然变化时速度矢量分布、粉尘运动轨迹和流线分布见图3、图4和图5。由图3和图4可见层流区位于回风巷中部，湍流区处于巷道边界，两帮和顶底板位置，在风流进入断面变化区域后，即出现了风流的涡流区，同时由于能量的损失，风速迅速减小。

4.2 回风巷断面突然变化模型粉尘浓度的分布规律

对回风巷粉尘浓度分布的三维模拟如图5所示：

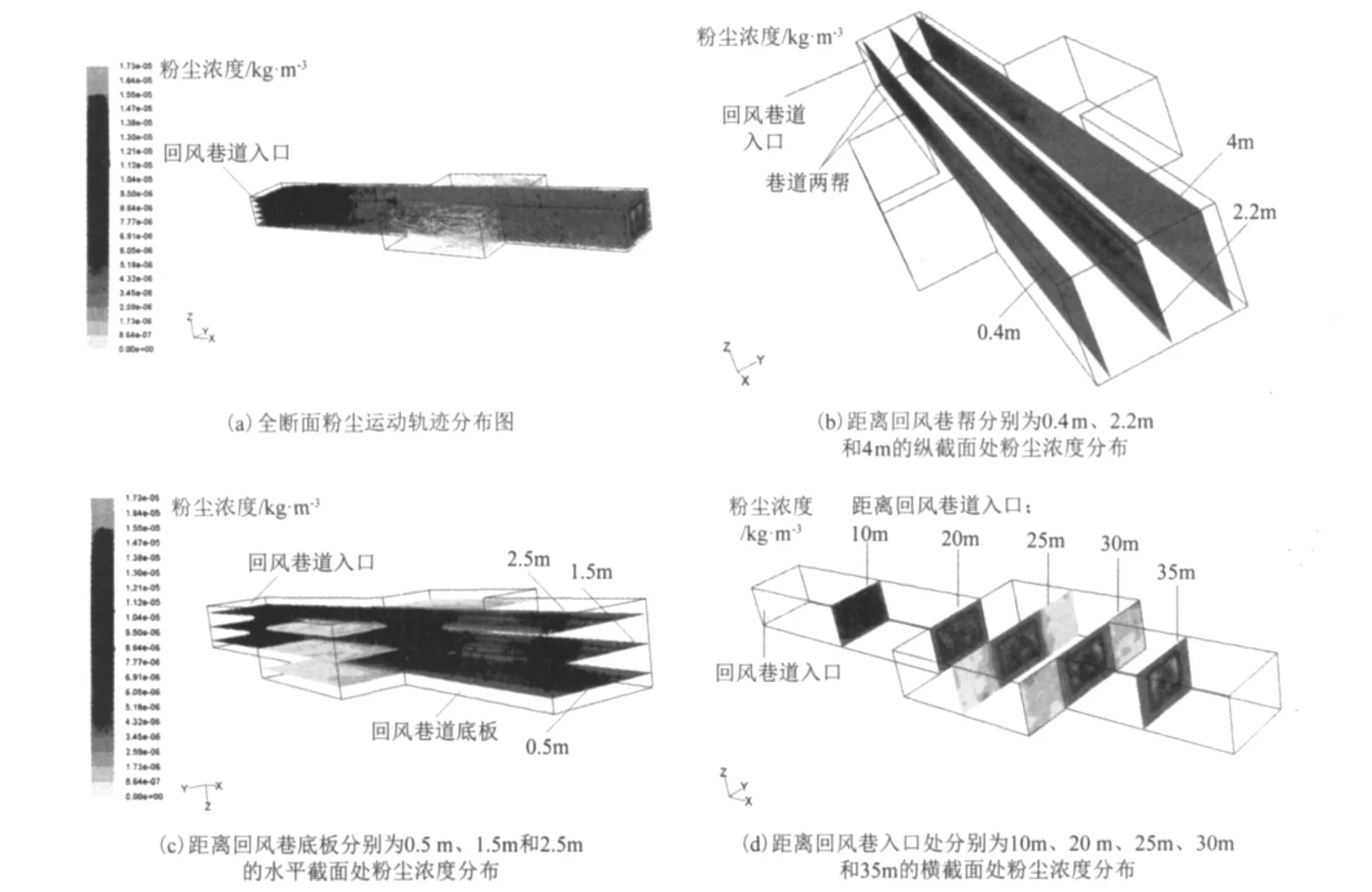
图5 跟踪断面突然变化粉尘运动轨迹分布图

由图5（a）可见，粉尘进入回风巷附近时浓度最大，其在风流作用下沿着巷道全断面不断前进，部分粉尘随着风流进入断面扩大区域后，受风流形成旋涡区的影响，粉尘开始旋转沉降和被捕集，因此粉尘浓度沿程不断减小；未沉降或被捕集的粉尘颗粒在随风流运动的同时，随机扩散，弥漫整巷道，使得巷道内的粉尘浓度趋于稳定。由图5（b）可见，粉尘从回风巷入口处进入后，靠近巷道两帮的粉尘浓度变化明显，沿程逐渐降低；位于巷道中间2.2m处的粉尘浓度随着距离的变化不明显。由图5（c）可见，回风巷区域内，距离巷道底板越近，因重力作用将要沉降的大颗粒粉尘越多，因此粉尘浓度越大；远离回风巷入口处，粉尘浓度随着高度的变化，粉尘浓度随之下降。由图5（d）可见，粉尘从回风巷入口处流入巷道断面面积突然变化区域前（10～20m），浓度粉尘变化不明显，在进入面积扩大区域后至距离回风巷入口35 m处时，粉尘浓度有明显降低。

4.3 回风巷断面突然变化粉尘沿程浓度分布规律的比较

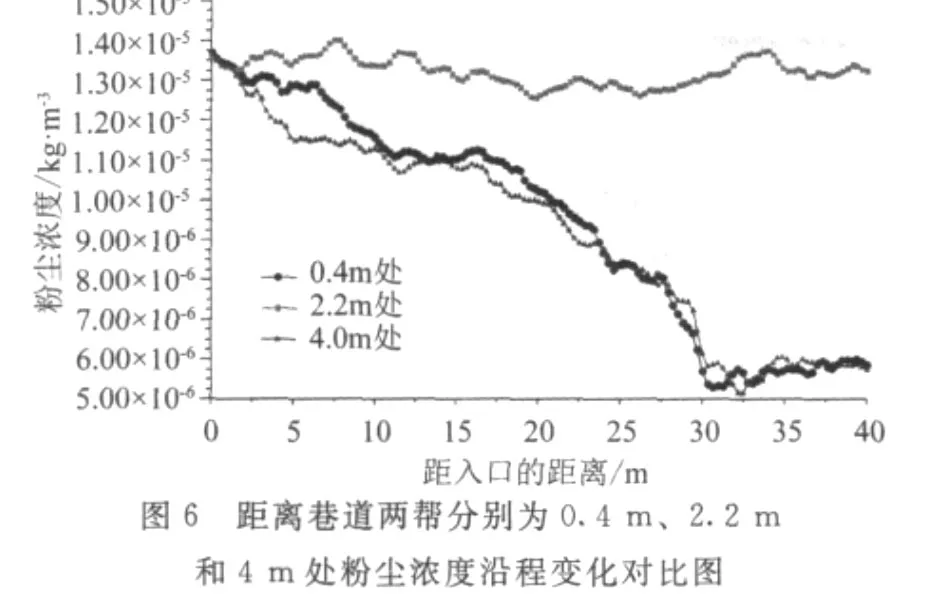
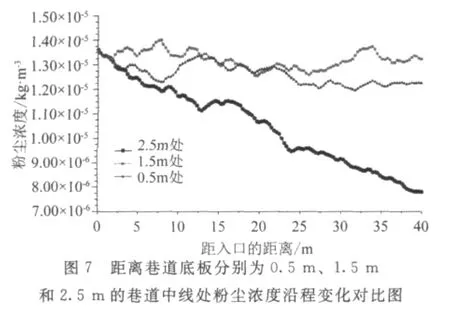
距离巷道两帮分别为0.4m、2.2m和4m处粉尘浓度沿程变化对比如图6所示；巷道中线处，距离巷道底板分别为0.5m、1.5m和2.5m的粉尘浓度沿程变化如图7所示。

由图6可见，在回风巷中，距离靠近巷道两帮越近，粉尘浓度越低，这种趋势在回风巷中面积扩大处25～30m之间较明显；从距离回风巷入口30 m处开始，靠近巷道两帮距离条件下，粉尘浓度都降到6mg／m3以下。

由图7可见，在巷道中线处，距回风巷入口处40m处，距离巷道底板1.5m处的粉尘浓度趋于稳定，距离巷道底板0.5m处的粉尘浓度由于受重力作用影响，粉尘在距入口10m处开始升高后，浓度沿巷道长度的增加，趋于不变；而从距离回风巷入口处开始，巷道顶部的粉尘浓度沿程稳定下降，基本都下降到8mg／m3以下。

5 结论

（1）在流体动力学中通风管道断面突变理论的基础上，首次结合两个学科，探索性地提出了利用回风巷断面突然变化段对巷道粉尘进行自然沉降的方法，既是理论的创新，又是科研探索的新方向。

（2）将巷道断面突然扩大段用在采煤工作面的回风巷处，在巷道中形成一道“无形透明屏障”，其降尘的方法并不是像固体壁一样阻挡粉尘的穿透，而是利用风流的不断旋转和风速的突然降低让粉尘颗粒自动沉降或撞在巷道两帮后失去能量后沉降，使得尘粒不能继续前移，以达到降低粉尘浓度的目的。

（3）利用回风巷道断面突然变化的降尘方法是针对贵州特定的地质条件特征提出的，在理论上切实可行，并且该方法若与风流净化水幕降尘技术相结合，不仅能提高降尘效果，而且能有效地减少巷道内由于降尘时喷雾所留下的积水，防止底板底臌，改善了井下作业的工作难度及工人的工作环境，更有利于煤矿的安全生产。

[1] 王晓珍.采掘工作面粉尘运动和分布规律的数值模拟研究[D].北京：北京科技大学，2007

[2] 刘毅，蒋仲安，蔡卫等.综采工作面粉尘浓度分布的现场实测与数值模拟[J].煤炭科学技术，2006（4）

[3] 陈卓如，金朝铭.工程流体力学[M].哈尔滨：哈尔滨工业大学出版社，1987

[4] 韩占忠，王敬，兰小平.FLUENT流体工程仿真实例与应用[M].北京：北京理工大学出版社，2004

[5] 江帆，黄鹏.FLUENT高级应用与实力分析[M].北京：清华大学出版社，2008

[6] 白兰永，王宽，周福宝，刘应科.综掘工作面综合降尘技术在葛泉矿的应用[J].中国煤炭，2011（7）

Numerical simulation of dust movement law and concentration distribution in return airway with sudden change of cross－section

Mo Fan1，Yu Zhongming1，Wu Guiyi2

（1.Architectural Engineering College，Guizhou University for Nationalities，Guiyang，Guizhou 550025，China；2.Mining College，Guizhou University，Guiyang，Guizhou 550003，China）

According to the theory of gas－solid flow，the dustfall via sudden change of crosssection in return airway was proposed.And the distribution of dust concentration in sudden enlarged cross－section of return airway was simulated by using discrete phase model of computational fluid dynamics.The concentration distribution and the variation law of dust in the return airway with sudden change of cross－section were summed up.

dust－proof in mine，gas－solid flow，hydrodynamics，sudden change of section

TD714

B

国家民委科研项目资助（编号09GZ03）；贵州省优秀科技教育人才省长专项资金项目资助（黔省专合字（2010）29号）

莫樊（1984－），男，贵州都匀人，硕士研究生，讲师，现贵州民族学院建筑工程学院工作，主要从事矿业系统工程和矿山安全方面研究。

（责任编辑 梁子荣）