半潜平台结构疲劳寿命评估方法比较

杨 鹏，顾学康

(中国船舶科学研究中心，江苏 无锡214082)

0 引 言

结构疲劳寿命评估是海洋结构物设计安全性评估的关键内容之一，如何准确有效地评估半潜式海洋平台的结构疲劳寿命是目前海洋工程界的一个难点。经典的结构疲劳寿命评估方法一般基于线性累积损伤原理和结构节点的S－N 曲线方法［1－3］，当前各大船级社［4－5］均推荐使用S－N 曲线方法进行船舶和海洋平台的结构疲劳寿命评估，有些船级社还使用断裂力学方法进行剩余疲劳寿命的评估。虽然S－N 曲线缺乏严格的理论依据且评估精度略差，但是由于经过了很长时间的发展，在工程上应用较为成熟。断裂力学方法能从机理上解释大量的疲劳现象，并且已经发展出了各种裂纹扩展模型，但是由于裂纹扩展机理本身十分复杂，因而现今还没有十分完善的模型和理论。然而断裂力学方法是最有希望解释清楚疲劳裂纹扩展现象的一种工具，因此很多学者一直致力于发展出可以更加精确的评估结构疲劳寿命的裂纹扩展模型。在海洋工程结构物疲劳寿命评估方面S－N 曲线方法和断裂力学方法存在多大的差别是有待研究考查的一个问题。另外，海洋结构物在随机波浪载荷作用下所承受的疲劳载荷的预报方法也有很多种模型，如谱分析方法、设计波方法、时域计算方法和DISAM 方法等［6］。谱分析计算方法简洁、高效，但是主要用于线性情况下。而时域计算方法过程合理但是计算费时，线性和非线性情况下均可使用。设计波方法是最为高效的方法，只需要给定一个或几个规则波中的波浪载荷分布并施加到结构模型上，然后计算结构应力即可进行结构疲劳寿命评估。设计波法的难点在于针对不同的结构部位确定不同的主要波浪载荷类型以及确定设计波浪向、波长和波高。ISSC 疲劳专家委员会［6］认为垂向弯矩、水平弯矩、扭矩、横向加速度和水动压力等均有可能成为关键波浪载荷参数，对于不同的船型、平台形式和构件，设计波浪载荷类型是不一样的，需要经过大量的计算论证。

因此，为了探讨S－N 曲线方法与断裂力学方法以及谱分析方法与设计波法在海洋结构物疲劳寿命评估方面的差别，本文分别利用S－N 曲线方法和断裂力学方法计算半潜式海洋平台的疲劳寿命，分析比较二者计算结果的差别。同时比较了谱分析方法和设计波法的计算结果，找出在使用设计波方法计算半潜式海洋平台典型节点的疲劳寿命时的主要波浪载荷参数，为半潜式海洋平台结构疲劳寿命的合理评估提供依据。

1 热点应力传递函数计算

某半潜式海洋平台总长114 m，总宽78 m，上甲板距基线高38 m，工作工况下设计吃水19 m，排水量5 万t，半潜式海洋平台的Ansys 整体和局部结构模型如图1所示。半潜式海洋平台有很多关键节点的疲劳寿命需要评估，本文以撑杆与立柱相接处的局部结构为例，选定1 根撑杆与立柱相接处的典型节点A(见图1)，进行疲劳寿命评估方法的比较与分析。

半潜式海洋平台的波浪载荷可以使用三维线性波浪理论进行计算［7］，虽然半潜式平台结构左右对称，但是在左右对称2 个浪向下，局部节点处的湿表面压力并不相同;同时相对浪向情况下，对于结构湿表面虽然波浪辐射势和入射势是一样的，但是绕射势存在一定差别，于是以上2 种情况下波浪载荷作用中局部节点的结构应力并不相同，因此需要对全浪向进行计算。计算浪向选定从0° ～330°每30°计算1 次，总共12 个浪向。计算波浪圆频率选定从0.01 ～1.6 rad/s，每0.05 rad/s计算1 次，总共31 个频率，该频率段包含了波浪的主要能量。

在单位波幅规则波下计算得到平台湿表面水动外压力和平台整体惯性力，水动外压力和平台整体惯性力按实部和虚部分别施加到平台整体有限元模型上。因计算平台湿表面水动压力的粗网格与平台外壳有限元模型的细网格不匹配，因此需要编制相应的水动压力载荷转换程序。通过转换程序计算平台湿表面上每个有限元单元的水动压力，然后使用APDL 语言编制相应的ANSYS 程序用于每个工况下的有限元结构应力计算和结构热点应力提取，同时应力选自shell63 单元的上表面。因为有12 个浪向，31 个频率，为了考虑不同部位水动压力相位的影响，响应计算分实部和虚部，取模即为热点应力幅值，所以总共需要进行744 次有限元应力计算。

有限元模型整体采用粗网格，在热点附近细化网格。热点处网格大小取板厚大小，网格尺寸依次向外平滑过渡，最后的有限元网格数约为10 万个。施加到有限元单元上的载荷有湿表面水动压力载荷和平台整体惯性力，然后在远离热点应力的结构上施加边界条件。计算得到的典型节点A 处各个浪向下的热点应力幅值Hs 的传递函数如图2所示。

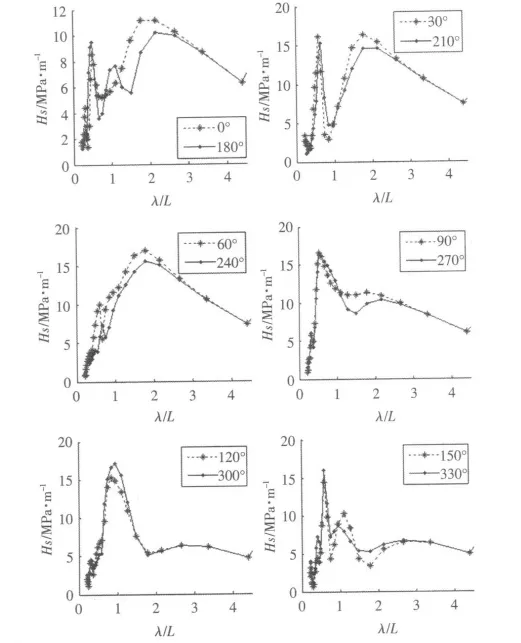
图2 热点应力幅值传递函数Fig.2 Transfer functions of stress amplitude at hot-spots

2 谱方法计算结构疲劳寿命

冯国庆［8］对疲劳强度评估中的谱方法流程进行了详细阐述，而马网扣［9］针对半潜式海洋平台典型节点的疲劳强度进行了谱分析，刘进喜等［10］使用谱分析方法研究了大型LNG 船典型节点疲劳寿命。深水海洋平台承受恶劣的风、浪、流环境载荷以及作业时的动态载荷等的作用，其中海浪的动载荷是引起疲劳的最主要因素，所以一般在海洋结构物疲劳强度研究中主要考虑海浪对疲劳损伤的作用，并且假定各个短期海况下的应力响应范围统计符合Rayleigh 分布，其概率密度函数形式如下:

式中:S 为应力范围;σ 为应力峰值均方差。选取中国南海波浪散布图［11］为该半潜式海洋平台的长期海况资料，海浪谱取JONSWAP 谱，谱峰提升因子取3.3。由波高和波浪周期表示的谱公式为

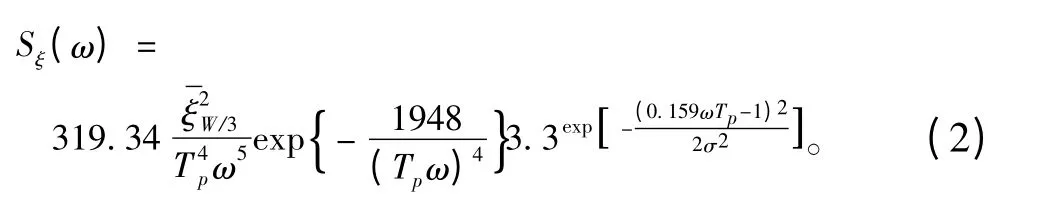
2.1 S－N 曲线计算疲劳寿命

对于特定海区作业的海洋平台，其服役期间所遭遇海况的长期分布可由该海区的波浪散布图确定。根据Miner 法则，总的疲劳应力参数可由各短期海况的疲劳应力参数线性叠加而得。考虑雨流修正和低应力范围修正后，结构疲劳应力参数可表达为［12］

式中:Ωj为某一浪向下的应力参数，总的疲劳应力参数其中q 为总的浪向数，pj为各浪向出现概率;σi为第i 个短期海况中交变应力Rayleigh分布的均方差;Γ 为伽马函数;f0i为各个短期海况的应力响应跨零频率;γi为各个有义波高HS 和过零周期TZ组合(短期海况)出现的概率;k 为波浪散布图中各短期海况总数;εi为带宽系数;λ(m，εi)为雨流修正系数。计算雨流修正系数的经验公式为

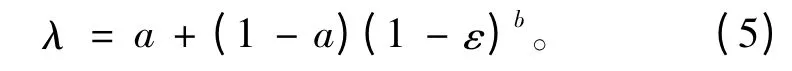
式中:a=0.926－0.033 m;b=1.587 m－2.323;m 为S－N 曲线SmN=A 的参数。Λi为考虑低应力范围的疲劳损伤修正系数［12］。

S－N 曲线方法中的疲劳寿命计算公式为［12］

式中Δ 为疲劳累积损伤因子，一般认为达到1.0 时结构发生了疲劳破坏。

2.2 裂纹扩展模型计算疲劳寿命

在采用裂纹扩展方法计算疲劳寿命时，Paris 模型最为常用。Paris 裂纹扩展公式为

式中:C 和m 为材料的裂纹扩展参数;Y(a)为几何修正系数;a 为裂纹长度;S 为应力范围。

考虑低应力范围的疲劳损伤修正后，结构的疲劳寿命为［12］

其中，与S－N 曲线方法类似有:

低应力范围的门槛值修正系数Λthi与裂纹长度a有关，可表示为

式中:Sth为应力范围门槛值;fs(S)为应力范围分布的概率密度函数即式(1)。

2.3 计算实例

前述半潜式海洋平台结构疲劳分析的参数选定如下:

1)S－N 曲线

选定DNV 规范［5］中的D 曲线参数，lgA=12.116，m=3，m′=5，SQ=52.63 MPa。板厚大于25 mm 时，采用以下应力范围修正公式

式中:S0为实际应力范围;T 为板厚。

2)Paris 公式

选定英国BS－2005 规范［13］中的裂纹扩展参数A=5.21 ×10-13，m=3，ΔKth=2 MPa·m0.5，板厚25 mm，初始裂纹深度为0.1 mm 或0.5 mm，几何修正系数参考文献［14］，即Y(a)=1.0a－0.125。

以上所有参数中，长度单位均为mm，应力单位为MPa。本文假设所有浪向出现概率均等。

计算得到的疲劳寿命结果见表1 和表2，从表1中可以看出2 种评估方法计算得到的疲劳寿命较为接近。该平台的设计寿命为30年，表1 中使用S－N 方法计算得到的结果表明A 点的疲劳寿命大于30年。

表1 初始裂纹深度为0.1 mm 时典型节点疲劳寿命Tab．1 Typical nodal fatigue life with initial crack depth 0.1 mm

表2 初始裂纹深度为0.5 mm 时典型节点疲劳寿命Tab．2 Typical nodal fatigue life with initial crack depth 0.5 mm

从表1 和表2 可以看出，使用断裂力学方法评估结构疲劳寿命时，初始裂纹深度的选取会对疲劳寿命评估结果产生较大影响。原因在于裂纹深度较小时，裂纹扩展速率较低，随着裂纹深度增长，裂纹扩展速率逐渐变大，因此裂纹穿透板厚的时间主要位于裂纹深度较小的扩展阶段。而初始裂纹深度有很大的随机性，与结构的类型、制造工艺、制造厂家和焊接工艺等大量因素有关，一般在0.1 ～1 mm 之间［12］，ABS 规范［4］推荐的初始裂纹在0.10 ～0.25 mm 之间，DNV 规范［5］推荐的为0.5 mm。而S－N曲线方法忽略了结构节点的初始缺陷情况，给出的是基于试验统计的具有一定置信度的疲劳寿命评估结果。综上所述在使用断裂力学方法时确定初始裂纹深度显得尤为重要，同时也说明S－N 曲线方法和断裂力学方法在评估疲劳寿命时没有绝对的可比性。

3 设计波法计算结构疲劳寿命

冯国庆和任慧龙［15］使用设计波法对某滚装船的典型结构进行了疲劳寿命评估，并且给出了使用设计波法计算船体结构疲劳寿命的详细流程，肖桃云等［16］基于设计波法对舰船整体结构进行了有限元分析，得到了全船的应力分布。李依阳［17］使用设计波法对船舶结构疲劳强度进行了评估，分别以船中处垂向波浪弯矩、水平弯矩、垂向剪力和水平剪力为设计波浪载荷对大量关键节点进行了疲劳寿命计算。结构疲劳分析中的设计波法主要源于如下观点:构件的结构应力主要由某种波浪载荷主导。疲劳寿命评估中的设计波法需要选定特征设计波浪载荷类型，然后计算波浪载荷传递函数，选定峰值最大点所对应浪向为设计浪向，对应的频率为设计波浪频率以及根据长期预报极值确定相应的设计波高，因此在载荷计算分析中首先需要计算波浪载荷传递函数。根据ISSC［6］的建议，本文在设计波法中分别以纵垂向弯矩、横垂向弯矩、中纵剖面的横向扭矩和撑杆与立柱节点处水动压力(图1 中A 点)为设计波浪载荷类型来计算结构疲劳寿命，因此需要计算4 种波浪载荷的传递函数。由于该半潜平台线型左右对称且前后基本对称，于是120° ～330°浪向的波浪弯矩或扭矩传递函数和0° ～90°的具有重复性，因此图3、图5 和图6 只给出0° ～90°的波浪弯矩或扭矩传递函数，而水动压力需要给出全浪向的值，计算得到的4 种传递函数如图3 ～图6所示。

一般情况下，使用设计波法计算半潜式海洋平台结构疲劳寿命过程如下:

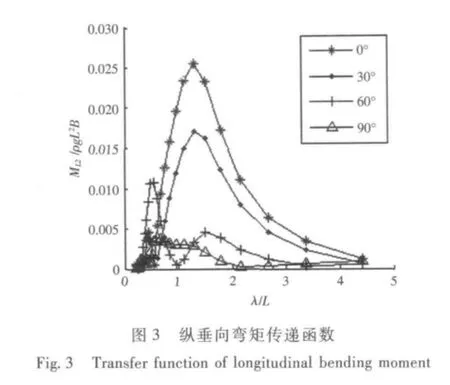
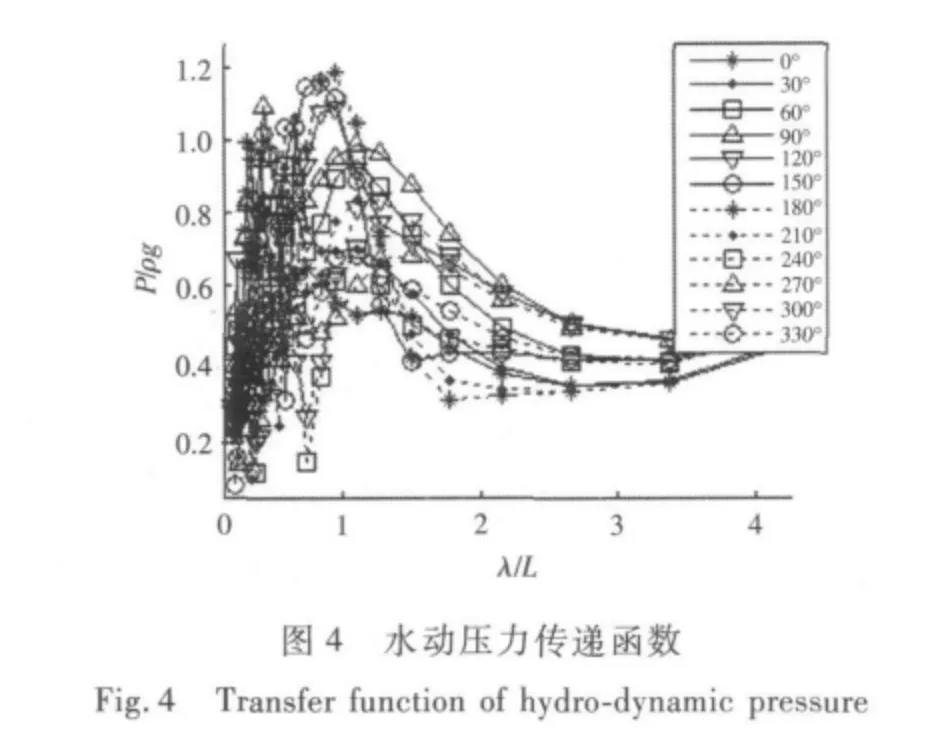
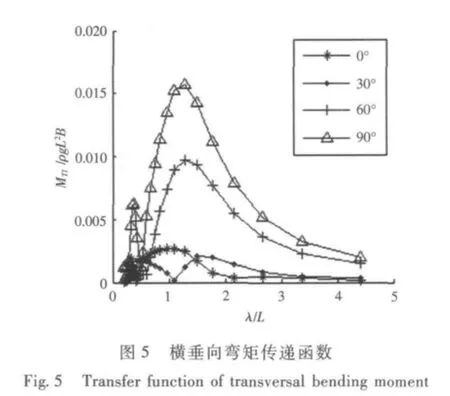
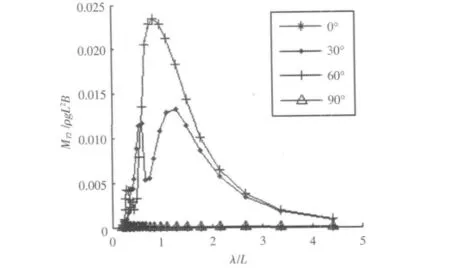
图6 横向扭矩传递函数Fig．6 Transfer function of transversal torsional moment

1)选择典型的海况资料，本文选取中国南海波浪散布图［11］。用三维势流方法计算平台在单位波幅规则波下的运动和波浪载荷传递函数。一般假设波浪载荷的长期分布服从Weibull 分布，然后对波浪载荷进行长期预报，取一定超越概率水平预报值作为设计值。按照ISSC［6］疲劳强度评估方法，这一概率水平取为10－4。油船和散货船共同规范疲劳评估中也推荐取概率水平10－4。目前正在协调的共同规范建议取超越概率为10－2，认为10－2超越概率水平的载荷对结构疲劳损伤的贡献最大，而且此时Weibull形状参数对疲劳寿命评估结果影响较小。但是本文认为对结构疲劳损伤的贡献率最大的超越概率不一定为10－2，这与形状参数和S－N 曲线的反斜率m有关。同时本文不认同10－2超越概率水平下，Weibull 形状参数对疲劳寿命评估结果影响最小的观点。基于以上分析，本文选取的超越概率水平为10－4。

2)设计波的浪向和频率根据设计波浪载荷的传递函数最大值决定。

3)设计波波幅等于设计波浪载荷的长期预报值除以对应传递函数的最大值。

4)对平台施加设计波浪向、频率和单位波幅下的波浪载荷，计算热点应力。

5)同等超越概率水平下的应力范围设计值为设计波波高乘上单位波幅下的热点应力。

6)假设平台结构应力范围长期分布服从Weibull 分布，其形状参数取波浪载荷长期预报结果所服从的Weibull 分布的形状参数。根据热点应力范围设计值和超越概率水平可以得到应力范围长期分布的Weibull 尺度参数，从而平台结构应力范围长期分布完全确定。

7)得到应力范围的长期Weibull 分布后，就可以通过式(13)计算等效应力［12］，然后使用S－N 曲线方法或断裂力学方法进行疲劳寿命评估。

式中:m 为S－N 曲线参数;ξ 为Weibull 分布的形状参数;SL为热点应力范围设计值即步骤5 的计算结果;NL为循环次数。

按照上述步骤计算得到不同设计波载荷类型下的设计波长、浪向、波高和Weibull 形状参数如表3所示，表4 给出了不同设计波参数下的热点应力幅值。

表3 设计波参数Tab．3 Design wave parameters

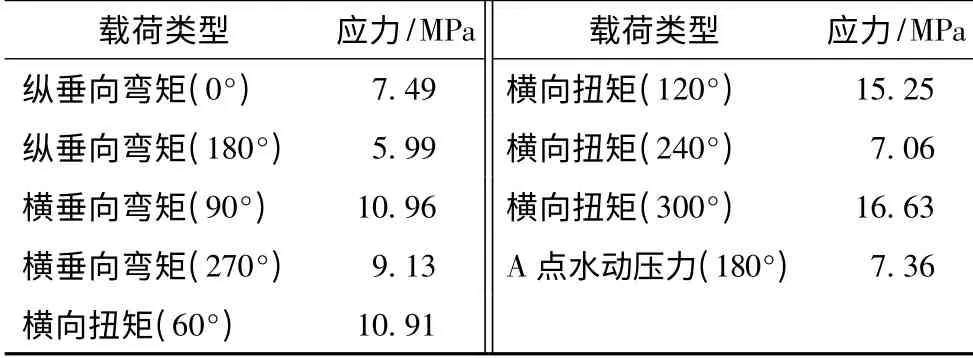
表4 热点应力幅值Tab．4 Stress amplitude in hotspot

根据表3 中的设计波参数，使用S－N 曲线方法分别计算得到节点的疲劳寿命见表5，使用断裂力学的Paris 方法分别计算得到节点的疲劳寿命见表6。从表5 和表6 可以看出以横向扭矩(60°)为设计波浪载荷，计算得到的疲劳寿命和表1 中使用S－N 曲线方法或Paris 方法计算得到的结果较为接近，可能原因在于横向扭矩对A 点的应力影响大。因此本文认为在使用设计波法计算半潜式平台撑杆和立柱交界处节点疲劳寿命时，设计波浪载荷类型应该选用横向扭矩(60°)。从表5 和表6 的计算结果还可以发现，即使对同样的载荷类型，不同浪向下的结构疲劳寿命计算结果也存在很大的差别，这是因为不同浪向下结构关键节点的热点应力响应差别较大(见表4)。例如纵垂向弯矩分别在0°与180°浪向计算得到的疲劳寿命，横垂向弯矩在90°与270°计算得到的疲劳寿命均差别较大。这可从波浪载荷的势流理论上进行解释，即针对平台上某一结构位置来说，相对浪向的波浪入射势和辐射势是相同的，而绕射势不同，这样在该点造成的结构应力也将不同。

从力学角度出发可以发现，横垂向弯矩主要使A 点局部结构产生弯矩应力，而横向扭矩主要使A点产生薄膜应力，对A 点来说横向扭矩导致的薄膜应力会大于横垂向弯矩引起的弯矩应力。虽然纵垂向弯矩也是使A 点局部结构产生总纵薄膜应力，但是由于A 点远离平台中横剖面，因此纵垂向弯矩引起的总纵薄膜应力应该较小。而局部水动压力使该处产生弯矩应力，其引起的弯矩应力较小。

表5 S－N 曲线计算的疲劳寿命Tab．5 Fatigue life in S－N curve method

表6 Paris 公式计算的疲劳寿命(初始裂纹长度0.1 mm)Tab．6 Fatigue life in Paris method with initial crack depth 0.1 mm

4 结 语

为了探讨船舶与海洋工程结构物疲劳强度分析中各种评估分析方法对疲劳寿命的影响，本文从疲劳载荷和疲劳损伤模式两方面对几种主要的疲劳寿命评估方法进行了比较分析。

采用S－N 曲线方法和Paris 断裂力学方法分别计算了某半潜式海洋平台典型节点疲劳寿命，经过比较分析后认为这2 种方法的计算结果较为接近，应用于评估半潜式海洋平台疲劳寿命均是可行的。同时发现裂纹扩展理论中，初始裂纹长度对最终的疲劳寿命评估影响较大。

通过波浪载荷的谱分析方法和设计波法分别进行了半潜式海洋平台撑杆和立柱交界处典型节点的疲劳寿命评估。比较谱分析方法和设计波法的计算结果后，发现设计波法中应以60°浪向的横向扭矩为设计波浪载荷来确定设计波参数。

今后尚需对半潜式海洋平台其他位置处的典型节点进行评估分析，以获得更具普遍性的分析结论。

［1］崔维成，等．船舶结构疲劳强度校核研究现状及我国的发展［J］．船舶力学，1998，2(4):63－81．

CUI Wei-cheng，et al．A state-of-the-art review for the fatigue strength assessment of ship structures［J］．Journal of Ship Mechanics 1998，1(4):63－81．

［2］XU T．Fatigue of ship structure details-technical development and problems［J］．Journal of Ship Research，1997，14(4):318－331．

［3］FRICKE W，CUI W C．Comparative fatigue strength assessment of a structure detail in a containership using various approaches of classification societies［J］．Marine Structures，2002，115:1－13．

［4］ABS．Fatigue assessment of offshore structures［S］．2003．

［5］DNV．Fatigue design of offshore steel structures［S］．2005．

［6］ISSC．Fatigue loading (COMMITTEE VI．1)［C］．Proceedings of 15 th International Ship and Offshore Structures Congress，San Diego，USA．2003．

［7］戴仰山，沈进威，宋竞正．船舶波浪载荷［M］．北京:国防工业出版社，2006．

［8］冯国庆．船舶结构疲劳强度评估方法研究［D］．哈尔滨:哈尔滨工程大学，2006．

［9］马网扣，王志青，张海彬．深水半潜式钻井平台节点疲劳寿命谱分析研究［J］．海洋工程，2008，26(3):1－8．

MA Wang-kou，WANG Zhi-qing，ZHANG Hai-bin．Study on spectrum-based fatigue life direct calculation for spots of deep-water semi-submerged drilling unit［J］．The Ocean Engineering，2008，26(3):1－8．

［10］刘进喜，唐永生，楼丹平，赵耀，叶恒奎．大型LNG 船典型节点疲劳寿命谱分析评估［J］．海洋工程，2010，28(3):86－90．

LIU Jing-xi，TANG Yong-sheng，LOU Dan-ping，ZHAO Yao，YE Heng-kui．Fatigue strength assessment of typical spots in a large LNGC based on spectral method［J］．The Ocean Engineering，2010，28(3):86－90．

［11］HOBGEN N，DACUNBA L F，OLLIVER H N．Global wave statistics(GWS)［M］．Brown Union Pub．，London，1986．

［12］胡毓仁，李典庆，陈伯真．船舶与海洋工程结构疲劳可靠性分析［M］．哈尔滨:哈尔滨工程大学出版社，2010．

［13］BS7910．Guide to methods for assessing the acceptability of flaws in metallic structures［S］．2005:57．

［14］KUNG C J，WIRSCHING P H．Fatigue and fracture reliability and maintainability of TLP tendons［J］．OMAE，Safety and Reliability，ASME 1992，II:15－21．

［15］冯国庆，任慧龙．船体结构疲劳评估的设计波法［J］．哈尔滨工程大学学报，2005，26(4):430－434．

FENG Guo-qing，REN Hui-long．Design wave approach for the fatigue assessment of ship structures［J］．Journal of Harbin Engineering University，2005，26(4):430－434．

［16］肖桃云，樊佳，梅国辉，侯国祥，陈力，张聪，胡奔．基于设计波法的舰船整船有限元强度分析［J］．舰船科学技术，2010，32(6):37－43．

XIAO Tao-yun，FAN Jia，MEI Guo-hui，et al．Strength analysis of overall ship FEM model based on design wave approach［J］．Ship Science and Technology，2010，32(6):14－19．

［17］李依阳．船舶结构疲劳强度评估的设计波法［D］．哈尔滨:哈尔滨工程大学，2010．