水下多智能体群协调控制仿真分析

张卫东，佘莹莹，唐正茂

(1．海军驻葫芦岛431 厂军事代表室，辽宁 葫芦岛125004;2．武汉第二船舶设计研究所，湖北 武汉430064)

0 引 言

随着应用的需要和技术的发展，多智能体系统的协调控制在世界范围内掀起了研究热潮。作为多智能体系统协调控制中的研究热点，一致性问题主要是基于多智能体系统中的智能体相互之间的信息交换，通过设计一致性协议使得所有智能体的状态达到某同一值。文献［1－6］对该问题做了大量的研究。

由于海底环境的复杂多变和无法预知，很多工作都不适合潜水员以及载人潜水器进行。作为海洋资源开发工具，水下智能体(AUV)成为当今各国在海洋工程领域中的研究热点。这主要是由于在实际的水下作业中，AUV 可以自主地运行在远程的、难于接近的、无法预知的或危险的海洋环境中，完成自主导航、自主避障和自主作业等任务。

本文主要研究在AUV 群按照给定规律运动时的稳定性问题。由于大多数一致性问题的研究都是假设最终达到的一致性值是固定不变的常数。在AUV群的运动控制中，要求系统在水中以规定的队列沿着指定的运动方式前行，此时，一致性问题的最终一致性值应随时间而动态变化。这里基于一致性理论的思想，在具有通信约束的情况下，对每个AUV设计1 个分布式控制器，使它们能按照给定的队列进行运动。

1 AUV 运动模型

在一般情况下，AUV 在水中的运动可看作刚体在流体中的空间运动。当AUV 在运动中的航向不变，仅改变深度时，其重心始终保持在同一铅垂平面内;在航向改变，深度不变时，AUV 的重心始终保持在同一水平面内。针对AUV 的运动模型(忽略横滚面的运动)，将AUV 在水中的空间运动进行近似处理，分解为水平面运动和垂直面运动。当AUVi以Vi的航速运动时:

对于其平面运动，用(ξi，ηi)，φi，βi，ri分别表示其重心的坐标、首向角、水动力角(漂角)及回转运动的角速度。可以得到:

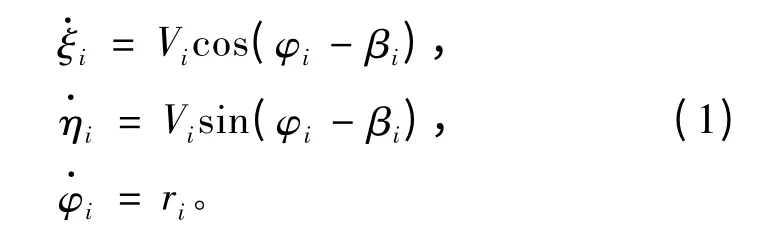
对于其垂直面运动，用(ξi，ζi)，θi，αi，qi分别为其重心的坐标、姿态角、水动力角(冲角)及纵倾运动的角速度。可以得到:

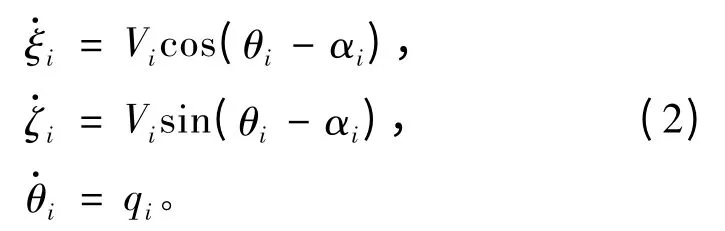
通常情况下，平面运动可以体现AUV 运动的基本特征——深度和航向的控制，而且空间运动的水动力特性也是在平面运动的基础上发展起来的。在本章中，主要研究AUV 平面运动的控制。要求AUV群的平面航速为v0，回转运动的角速度为r0，垂直速度为vζ0，根据式(1)和式(2)可以得到第i 个AUV 的动态模型为:

式中参数α*为正参数。用(ξfi，ηfi)表示AUVi 上与重心(ξi，ηi)相距di的点fi的位置。此时，在对AUV的协调控制中，可用(ξfi，ηfi)替代(ξi，ηi)，以简化协调控制算法的设计。

当系统要求的参数满足

通过变换可以得到:

可以看出，通过设计uξi，uηi和uζi的控制算法就能对AUV 群进行协调控制。在对AUV 群运动控制的分析中，假设每个AUV 都具有唯一的与之对应的编号且每个AUV 都知道自身及与其邻域内的AUV的编号。另外，所有AUV 之间的相互作用都是同步的，即所有AUV 都是在同一时刻更新其状态参数。

2 具有通信约束的AUV 群运动算法

由于AUV 的通信能力较为有限，特别是在水下通信受到很多约束，这里针对具有通信约束的AUV群设计了一类分布式控制器，当AUV 间的通信时滞在一定范围内，所有的AUV 仍然能按照期望速度和队形进行稳定的运动。假设所有AUV 都在给定水深进行运动，即ζi为一给定值。当AUV 间的通信存在时滞时，设计了如下分布式控制器:

式中:控制增益γ ＞0，τij(t)为AUVi 和j 之间通信时滞;fξ(t)，fη(t)为连续可微的函数，表示AUV 的运动速度特性，并且对所有AUV 来说，其运动速度特性的描述都是一样的;和为AUVi 在1 个静态坐标系统中期望队形中的位置，为一时不变的函数。假设任意2 个不同AUV 之间通信允许1 个共同时滞上界τ0，即0 ≤τij(t)≤τ0。在其个体间的通信时滞τij(t)满足:

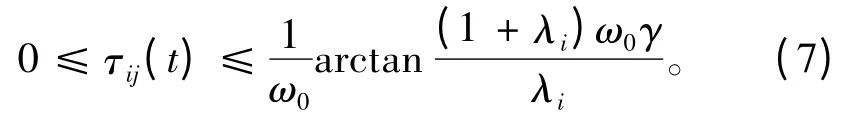
3 仿真分析

假设AUV 群有6 个AUV，其编号分别为1，2，3，4，5，6。其无向连通通信网络拓扑结构图如图1所示，其邻接权重均为1。

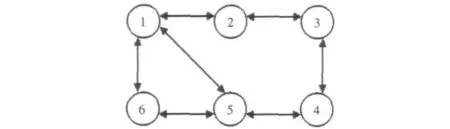
图1 无向连通网络拓扑结构图Fig．1 A undirected connected communication graph

此时图1 对应的Laplacian 矩阵的特征值分别为:λ1=0，λ2=1，λ3=1.585 8，λ4=3，λ5=4，λ6=4.414 2。当系统的控制输入uξi和uηi分别为式(5)和式(6)时，根据式(7)可知系统的时滞上界为τmax(t)=0.37。选取γ=1，AUV 之间的时滞为:τ12(t)=τ21(t)=0.1，τ15(t)=τ51(t)=0.2，τ16(t)=τ61(t)=0，τ23(t)=τ32(t)=0.1，τ56(t)=τ65(t)=0，τ34(t)=τ43(t)=0.2，τ45(t)=τ54(t)=0.1。系统初始状态随机给定。跟随AUV 之间的相对位置满足:δ1。AUV 的运动速度特性为fξ(t)=tsint，fη(t)=cost。图2 ～图5 分别给出了系统在控制输入uξi和uηi下的位置和速度信息。

从图2 和图4 可以看出，所有个体最终能保持稳定的队形，图3 和图5 显示了个体之间最终速度能达到一致，图6 给出了系统平面运动的轨迹。

为了验证理论结果的正确性，对个体间时滞超出定理1 给出的时滞上界时的仿真结果，此时选取所有的个体间的时滞都为0.4。图7 给出了τij=0.4 时系统平面运动的轨迹。

对比图5 和图7 可以得出，只有在个体间时滞小于式(7)给出的时滞容忍上界时，系统才能形成稳定的编队。

4 结 语

本文在具有通信约束的情况下，基于局部信息，对每AUV 设计1 个分布式控制器，使AUV 群能很方便地实现队形控制和群运动控制。给出了一个任意2个AUV 之间进行通信所允许的时滞上界的具体解析表达式，通过计算机数值仿真分析证明了针对AUV群所提出的分布式控制器的有效性。

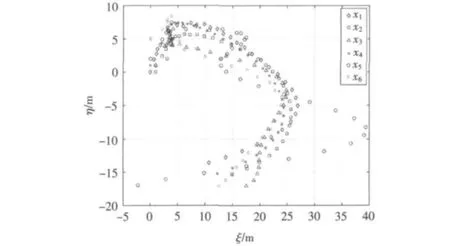
图7 系统平面运动轨迹τij=0.4Fig．7 The plane tracking of the system under τij=0.4

［1］VICSEK T，CZIROK A，et al．Novel type of phase transitions in a system of self-driven particles［J］．Physical Review Letters，1995，75(6):1226－1229．

［2］REN W，et al．Consensus seeking in multi-agent systems under dynamically changing interaction topologies［J］．IEEE Trans．on Automatic Control，2005，50(5):655－661．

［3］XIAO L，et al．Fast linear iterations for distributed averaging［J］．Systems ＆ Control Letters，2004，53(1):65－78．

［4］LIU C L，TIAN Y P．Coordination of multi-agent systems with communication delays［A］．IFAC World Congress［C］．Seoul，2008．10782－10787．

［5］XIE G，WANG L．Consensus control for a class of networks of dynamic agents［J］．International Journal of Robust and Nonlinear Control，2007，17(10－11):941－959．

［6］TANNER H G，et al．Flocking in fixed and switching networks［J］．IEEE Trans．on Automatic Control，2007，52(5):863－868．

［7］施生达．潜艇操纵性［M］．北京:国防工业出版社，1995．