基于熵满意度的多信息协同决策方法
2012-12-02张福光刘士新王新政
单 鑫,张福光,刘士新,王新政
(1.海军航空工程学院,山东 烟台264001;2.中国人民解放军91980 部队,山东 烟台264001)
0 引 言
决策协同是指具有不同知识水平、经验、思维方式的决策人员集中对方案进行评价,一般的做法是根据各决策者或专家的偏好信息判断矩阵采用不同的方法来集成。然而不同专家给出的判断矩阵可能形式不同,因此目标旨在寻找各决策者之间的平衡,科学合理地进行不同形式信息的转化,建立群体综合满意度最大的认知。本文针对区间互反与互补这2 种形式建立相应的满意度函数,并构建以满意度为目标的线性规划模型,结合熵理论解决信息协同的不确定性。
1 模型的建立
1.1 满意度函数
假设备选决策方案集为X={x1,x2,…,xm},现有n 个专家对备选决策方案进行协同决策,专家集合记为Y={y1,y2,yc,yc+1,…,yn},设专家k=1,2,…,c 提供区间数互反判断矩阵形式判断信息,专家k=c+1,c+2,…,n 提供区间数互补判断矩阵形式判断信息,则专家Yk对备选方案给出的判断矩阵形式可表示为
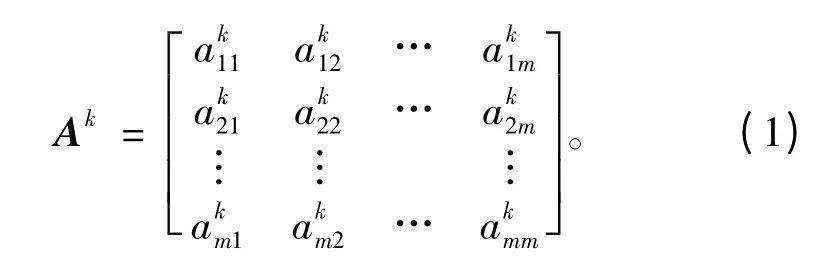
1)区间数互反判断矩阵
定义1[1]:称判断矩阵A=(Aij)m×m为区间数互反判断矩阵,如果它满足①Aii=1;②③Aij=1/Aji。
通常人们假设方案最终排序向量的比值在整个区间内的满意度均相同,但根据Hauser 的研究结论[2],往往这个比值越是接近区间中值专家会觉得满意度越高,这符合人们的思维和认知习惯。因此,在假设专家对区间中值满意度最高的基础上,对于最终排序向量w=(w1,w2,…,wm)T,构造满意度函数为[3]
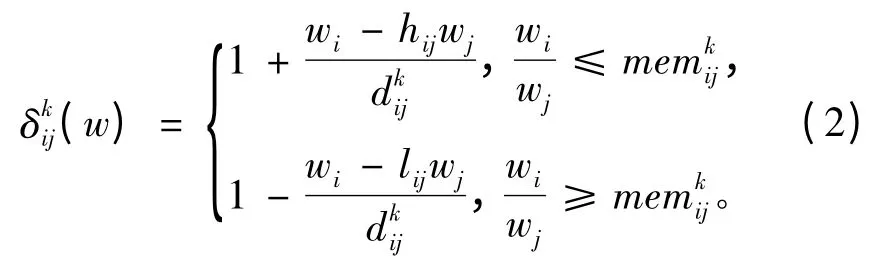

图1 满意度函数图像Fig.1 Graph of satisfaction degree function
2)区间数互补判断矩阵
定义2[1]:称判断矩阵A=(Aij)m×m为区间数互补判断矩阵,如果它满足①Aii=[0.5,0.5];②Aij=1-Aji,i≠j;③。
对于根据区间数互补判断矩阵得出的最终排序向量w=(w1,w2,…,wm)T,构造满意度函数为
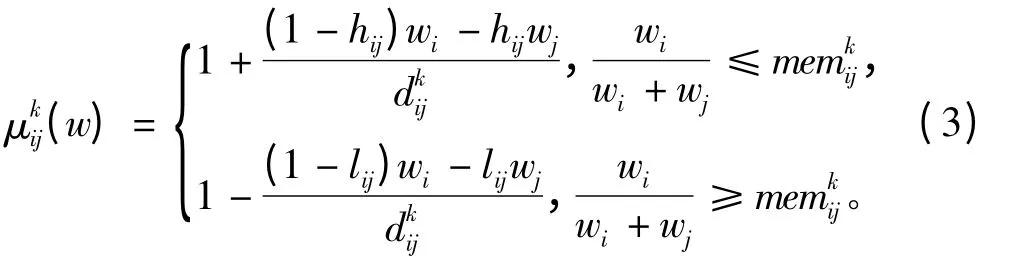
式(3)与式(2)性质相同,限于篇幅,这里不再进行说明。若令hij=0.35,lij=0.55,dij=0.15,则满意度函数的图像如图2所示。

图2 满意度函数图像Fig.2 Graph of satisfaction degree function
1.2 以满意度为目标的线性规划模型
根据上节满意度函数定义,可定义专家yk满意度函数的可行域为[4-5]
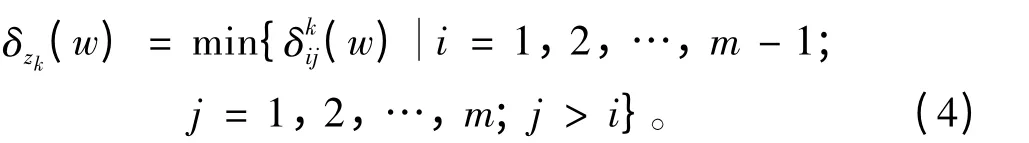
根据给出判断信息的不同,将整个专家全体划分为2 组,称为群体1 与群体2。对于群体1,其可行域可表示为,相应的群体1 满意度函数的可行域为
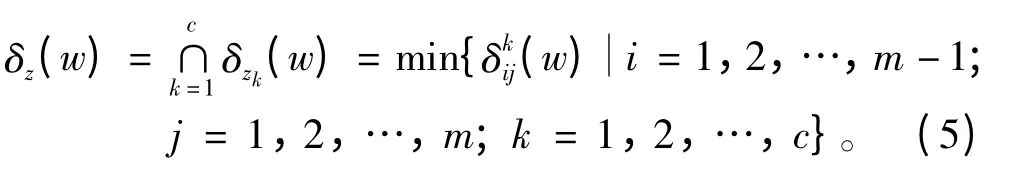
在上述群体1 可行域必存在权向量w=(w1,w2,…,wm)T,使得下式成立:

同理,对于群体2,也存在λ2成立,于是构造群体1 和群体2 的线性规划模型使得各群体的满意度达到最大:

1.3 各群体的综合协同决策
由于参与决策的专家给出的判断矩阵形式不同,而且不同群体重要度等可能并不相同,为了处理存在的这种信息不确定性,采用熵理论来对各群体的决策信息进行综合协同,以得到最优方案。
若设各群体的重要度加权系数η={η1,η2},则η2=1-η1,根据式(7)和式(8)可求得方案的权向量分别为),建立群体1 与群体2 的综合协同决策模型为:
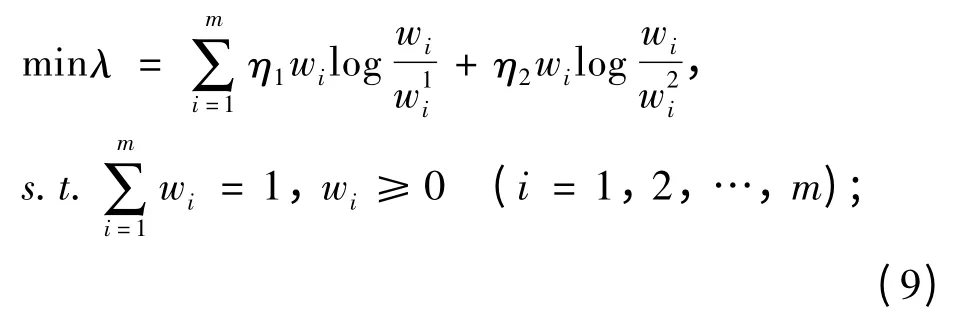
根据文献[6]可知,此模型存在全局最优解

2 实例分析
战时需要选择恰当的装备保障方案以保证整个保障活动的顺利进行,假设现存在4 个备选保障方案为A,B,C,D,有2 名保障领域专家和1 名指挥员根据自己的知识和经验对方案分别进行判断决策,设保障领域专家给出的是区间互反判断矩阵,而指挥员给出的是区间互补判断矩阵,各矩阵信息如表1所示。
w1=(0.559 4,0.084 6,0.241 6,0.114 4)T,λ1=0.888 7;
w2=(0.424 2,0.066 0,0.336 9,0.172 8)T,λ2=1.028 0。
根据式(10)求得最优解为
w*=(0.506 7,0.077 5,0.279 3,0.136 5)T。
因此,保障方案排序关系为A >C >D >B。此外在进行协同决策时,可以通过改变允许判断偏差来反映参加决策的人的知识、背景、经验等差异,若进行综合协同决策后的满意度为负,说明对此结果并不满意,此时需要各决策者进行协商来解决[7]。
3 结 语
本文针对区间互反与互补判断矩阵2 种不同形式的偏好信息的协同决策问题,给出了2 种不同的满意度函数,并将线性规划模型与熵理论进行结合建立了各群体的综合协同决策模型,求得的最优解能最大程度地满足群体满意度目标,可为战时保障指挥决策提供参考。实例表明该方法操作简单,下一步应针对更多形式偏好信息的满意度函数进行研究,以便适应更多决策者的思维判断习惯,使决策更为科学合理。

?
[1]史文雷,吕跃进,徐改丽.区间数互补判断矩阵中元素的运算与排序算法[J].广西科学院学报,2007,23(1):20-22.
[2]HAUSER D,TADIKAMALLA P.The analytic hierarchy process in an uncertain environment:a simulation approach[J].European Journal of Operational Research,1996,91(1):27-37.
[3]MIKHAILOV L.A fuzzy approach to deriving priorities from interval pairwise comparison judgements[J].European Journal of Operational Research,2004,159(3):687-704.
[4]MIKHAILOV L.Group prioritization in the AHP by fuzzy preference programming method[J].Computers &Operations Research,2004,31(2):293-301.
[5]KUMAR M,VRAT P,SHANKAR R.A fuzzy goal programming approach for vendor selection problem in a supply chain[J].Computers & Industrial Engineering,2004,46(1):75-76.
[6]魏存平,邱菀华.群决策问题的REM 集结模型[J].系统工程理论与实践,1998,19(8):38-41.
[7]刘明广,杜纲.基于满意度最大的群决策方法[J].系统工程,2005,23(5):111-114.
