引入加速度的无人机皮托－静压管法测风模型

金永奇，周树道，卫克晶，王迎强

（解放军理工大学气象学院，江苏 南京 211101）

0 引言

气象无人机是在无人机技术和气象探测技术的基础上发展起来的一种新型大气探测设备［1］。由于它具有可重复使用、按指定航线探测、低成本、智能化等特点，近年来得到了迅速的发展，已成为一种新的大气探测平台。当前在进行无人机气象探测中，对于温压湿等物理参数测量已取得了较好的效果，但在测风的使用上，精度还有待提高。

当前无人机测风主要使用的是皮托－静压管法，通过测得的空速、地速来计算出风速。但该方法存在着精度较低的问题，有时甚至误差无法被容忍。为了提高无人机测风的精度，本文对原有测风模型进行重新分析，对产生的误差来源进行寻找，并针对误差来源对模型进行改进。

1 现有测风模型分析

无人机的皮托－静压管测风方法主要是测得空速和地速两个矢量，再通过矢量运算得到风速。图1为地速、空速、风速的矢量关系图。

风速计算公式［2］为：

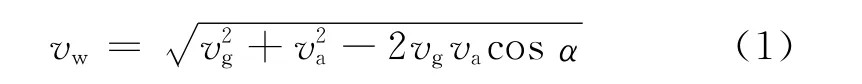
式（1）中，vw为风速；vg为地速；va为空速；α为空速和地速夹角。地速采用读取安装的无人机上的GPS模块输出的数据直接得到，而空速通过测量静压、静温和差压等间接计算得到。

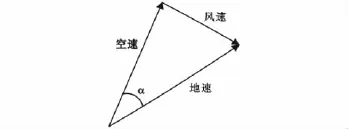
图1 地速、空速和风速矢量图Fig.1 Ground speed，airspeed，and wind speed vector

采用皮托－静压管测量空速的结构［3］如图2。当无人机飞行空速小于400km／h，可以认为空气没有被压缩，其密度不变［4］，在这种情况下，空速计算公式为［5］：

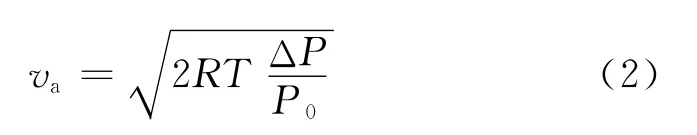
式（2）中，R 为气体常数，对于理想大气R ＝287.052 87m2／（K·s2）［6］；T为静温；ΔP为动压，即总压与静压之差；P0为静压。

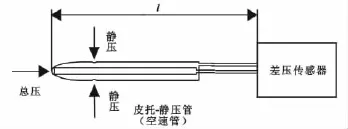
图2 空速测量结构图Fig.2 Airspeed measurement structure diagram

风速误差主要来源于空速和地速。由于速度是矢量，误差包括大小和方向两个方面，而这里仅对空速和地速的大小误差导致的风速误差作一考虑，暂不考虑角度导致的误差。

地速采用GPS测得，GPS的信号有两种码：P码和C／A码，目前民用的为C／A码，其定位误差在29.3～2.93m，测速精度达0.3m／s［7］，对风速的传递误差［8］为：

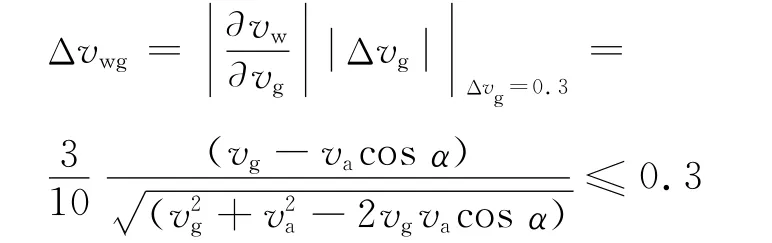
若风速为6m／s（4级风风速）时，地速误差导致的空速误差已很小，故对地速的测量方法不作改动。而空速计算公式建立在无人机匀速飞行的前提条件下，忽略了加速度对空速测量的影响。而实际上无人机在飞行过程中，由于控制算法和外界的干扰等原因，控制器会根据设定的时速不断调节飞行速度，使得无人机在飞行过程中很难达到匀速运动状态。为此，我们需引入加速度，对空速的计算模型进行重新推导并改进。

2 引入飞机加速度的改进模型

当飞机以大小为a，方向沿飞机皮托管纵轴的加速度飞行时，因为静压孔与加速度方向垂直，故加速度对静压大小的测量没有影响，而总压方向上的受力情况将发生改变。在皮托管的动压管中的气体除受到原有的压力外，还将受到一个导致这部分气体产生加速度a的额外作用力。下面对总压管及连接到差压传感器管中的空气进行受力分析。

假设皮托静压管前端口到差压传感器这段空间是一个截面积为S，长为l的圆柱体。加速度a方向在该圆柱体轴向上，设m为该圆柱体内的空气质量。

总压主要来源于两部分：一是静压，其由该位置存在大气压力所导致；二是动压，由于飞机相对于空气存在速度，使得空气对飞机有一个作用力，阻碍两者相对运动，一般情况下其大小与飞机相对速度的平方近似成正比，具体为：

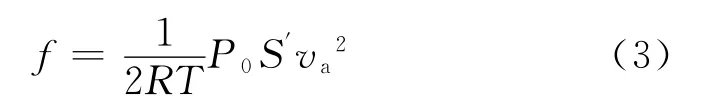
式（3）中，S′为迎风面积（这里S′＝S）；va为相对空气速度（即空速）。加速度对总压没有影响，但由于该圆柱体内的空气相对飞机静止，具有一个与飞机相同的加速度a，故受到了一个额外的力am，图3为皮托静压管前端口到差压传感器这段空间内空气运动方向的受力图。

图3 总压管中空气m在运动方向上的受力分析图Fig.3 Force analysis diagram in direction of motion of air in the total pressure tube

图3中，F1＝am＋P0S＋f为飞机对这部分空气作用的力，F2＝P0S＋f为大气对这部分空气的压力。此时飞机传感器测得的总压不再是F2／S，而是F1／S，差压传感器测得的差压ΔP＝F1／S－P0。则：

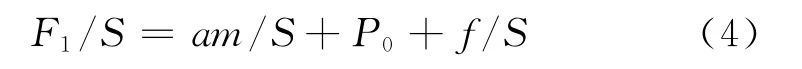
又ΔP＝F1／S－P0，所以得到了引入飞机加速度的空速计算公式：

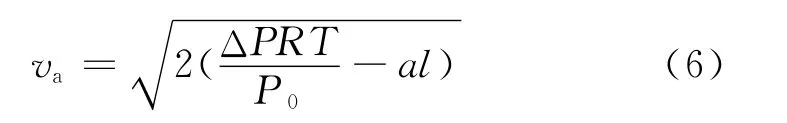
则原空速计算公式导致的误差为：

空速误差对风速的传递误差为：

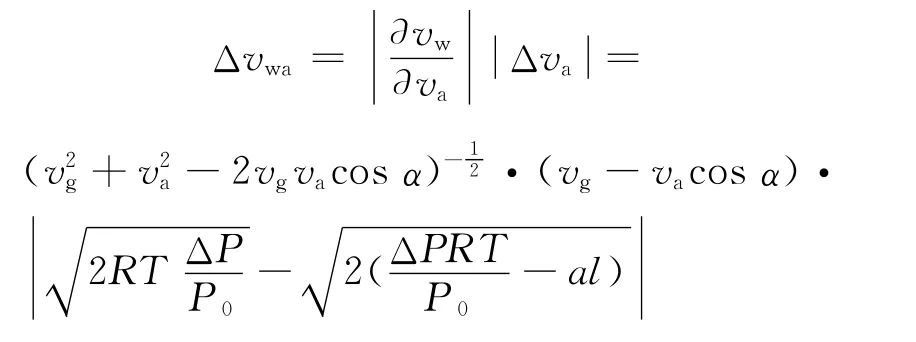
由此可知加速度对于空速测量存在着一定的影响，而现有的空速测量模型忽略了加速度这个物理量，只是一种近似的计算方面，存在着系统误差，而该误差也会传递给风速，最终影响着风速的测量结果。而改进后的模型引入了飞机加速度，消除了该系统误差。

3 定量计算及分析

为了观察不同空速和加速度情况下加速度对风速测量结果的影响，下面根据实际情况取一系列值进行定量计算，显示出各关系图，从而可直观地看出改进模型对减小误差所取得的效果。这里根据小型气象无人机的外形尺寸将l取为5m，又根据无人机的飞行参数，取飞机空速为26～42m／s，加速度为－9.5～10m／s2。分别对不同加速度和空速下的空速误差进行分析，最后得出不同风速下的风速相对误差。

3.1 不同加速度下的误差计算分析

根据无人机一般的巡航速度在120km／h（即33 m／s）左右的特点，这里假设飞机空速为30m／s，计算在不同加速度下的空速误差。得到空速误差与加速度的关系曲线如图4所示。

通过对图4的观察可知，加速度导致的空速误差绝对值随加速度绝对值的增加而增加，其值在3 m／s以内。这个值相对于空速而言较小，甚至可以忽略不计，这也正是在经典的空速表中没有使用加速度对空速修正的一个原因。

图4 空速误差与加速度的关系图Fig.4 The Relationship diagram between airspeed error and acceleration

3.2 不同空速下的误差计算分析

假设飞机加速度值为6m／s2，计算不同空速下的空速误差大小，结果如图5所示。

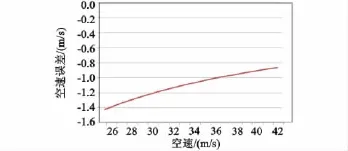
图5 空速误差与空速的关系图Fig.5 The Relationship diagram between airspeed error and airspeed

由图5可知，空速误差随空速的增加而减小，变化区间在－1.42～－0.86m／s。

3.3 不同风速下的相对误差计算分析

从以上两方面的分析，可以发现，虽然加速度导致的空速误差对于空速影响并不大，但是由于风速本身值相对较小，空速的这部分误差对于风速测量结果的影响将会出现不同的结果。根据前面的分析，取空速误差为上述计算中的平均值1.1m／s，当α接近于零时，对不同风速下的风速相对误差进行计算分析，结果如图6所示。

由此可知，忽略加速度而引起的风速测量相对误差比较大，有时甚至可以超高50%，平均误差也达到了22.83%。因此，对于测风而言，不能再使用原有的空速计算公式，而引入加速度从而提高风速测量精度是十分必要的。

图6 各风速下的风速相对误差Fig.6 Relative error of different wind speed

4 结论

本文通过对现有气象无人机测风模型及其误差的分析，找出了误差主要来源。进而针对该误差提出了引入加速度的无人机皮托－静压管法测风的改进模型。定量计算结果表明：改进后的模型可以消除的误差平均为22.83%，最高甚至可达50%，从而表明了改进模型的实际意义，也为提高现有的气象无人机测风设备的测量精度提供了一个很好的改进方向。

［1］沈怀荣，邵琼玲，王盛军.无人机气象探测技术［M］.北京：清华大学出版社，2010.

［2］周伟静，沈怀荣.一种基于小型无人机的风场测量方法［J］.测试技术学报，2009，23（4）：297－302.ZHOU Weijing，SHEN Huairong.A wind measuring method based on a Mini－UAV［J］.Journal of Test and Measurement Technology，2009，23（4）：297－302.

［3］韦良耶夫斯卡娃.航空仪表与自动驾驶仪［M］.张宗汉，王若松，译.北京：国防工业出版社，1957.

［4］王成豪.航空仪表［M］.北京：科学出版社，1992.

［5］樊尚春，乔少杰.检测技术与系统［M］.北京：北京航空航天大学出版社，2005.

［6］黄成功，邵琼玲.小型无人机空速测量系统设计［J］.计算机测量与控制，2009，17（8）：1 512－1 516.HUANG Chenggong，SHAO Qiongling.Design of airspeed measuring system for small unmanned aerial vehicle［J］.Computer Measurement ＆ Control，2009，17（8）：1 512－1 516.

［7］李天文.GPS原理及应用［M］.北京：科学出版社，2003.

［8］康学政.测量误差［M］.北京：中国计量出版社，1990.