基于小波-BP神经网络的风电场短期风速预测

胡晓虎

（铜陵有色金属集团股份有限公司，安徽 铜陵 244000）

由于风能的随机性和不可控性，风电厂出力也在随机的变化。随着风电装机容量的日益加大，风力发电的随机性和波动性必然会对地区电网产生不良影响。对风速的预测可以有效减轻和预防这种不利影响[1]。常见的风速预测方法有时间序列法[2]、人工神经网络法[3]、卡尔曼滤波算法[4]、支持向量机法[5]等。其中，BP神经网络法在风速预测中表现出较好的性能,因此得到了广泛的应用。

小波变换[6，7]是当前数学中一个迅速发展的新领域，它同时具有理论深刻和应用广泛的双重意义。小波变换是一个时间和频率的局域变换，因而能有效地从信号中提取信息，通过伸缩和平移对函数或信号进行多尺度分析。小波分析在许多领域都取得了具有科学意义和应用价值的重要成果。

由于风速时间序列波动较大，采用单一的神经网络模型预测精度较低。将小波技术和神经网络相结合可以有效提高风速预测精度。本文将小波多分辨率分析技术和BP神经网络相结合，提出一种小波-BP神经网络预测模型，即用小波分解技术将风速序列分解成基础分量和细节分量，然后对各分量分别用BP网络进行预测，最后经重构得到原始风速序列的预测值。本文将该方法应用于实际风电场短期风速预测，取得了很好的效果。

1.BP神经网络

BP（Back Propagation）神经网络可以以任意一个精度去逼近所有的非线性映射，适用于比较复杂的非线性系统的模型建立和预测[8]。BP神经网络是基于误差反向传播算法的人工神经网络，包含了输入层、中间层(隐含层)和输出层。BP神经网络学习过程分正向传播和反向传播，即信息的正向传播和误差的反向传播两个过程组成。BP神经网络可以有多层，但以三层最为常见，其结构如图1所示[9]。

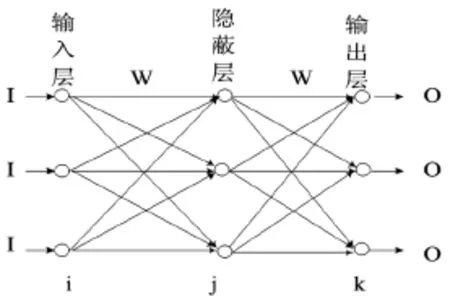
图1 三层BP神经网络示意图

输入层的神经元为i，隐蔽层的神经元为j，输出层的神经元为k。隐蔽层第j个神经元的输入为：

BP学习过程中的误差反向传播过程是通过使一个目标函数（实际输出和希望输出之间的误差平方和）最小化来完成的，采用梯度下降法进行训练。

设第k个神经元的希望输出为tpk，而网络输出为opk，则系统平均误差为：

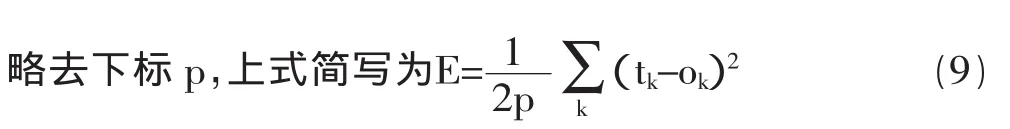
根据梯度下降法，权值的变化项Δwkj与鄣E／鄣wkj成正比，即

式中E为目标函数。

由式（9）和式（10）可知

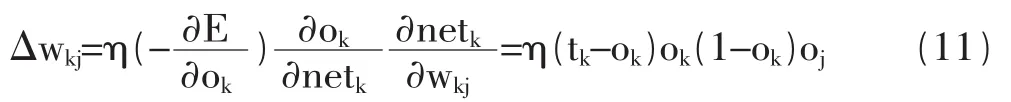
对于隐蔽层神经元，也可以写成

则各个权重系数的调整量为：

2.小波分解与重构

小波分析在时域和频域同时具有良好的局部化性质，对高频成分在时域中采用逐渐精细的分析步长，对低频成分则采用较粗的分析，因此对此类数据能够表现出一定的自适应能力。

设，Ψ（t）∈L2（R），L2（R）表示平方可积的实数空间，即能量有限的信号空间，其Fourier变换为（w）。当（w）满足容许性条件：

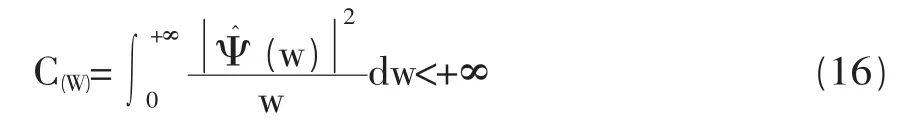
此时，称 Ψ（t）为母小波（Mother Wavelet），因为对Ψ（t）做平移，伸缩可以得到小波函数：

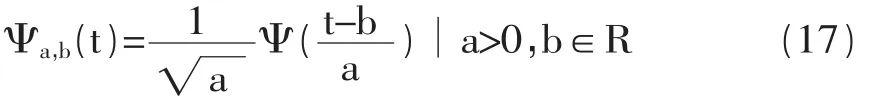
其中，a为伸缩因子或尺度因子，b为平移因子。

连续小波变换(Continuous wavelet transform，CWT)的定义为：

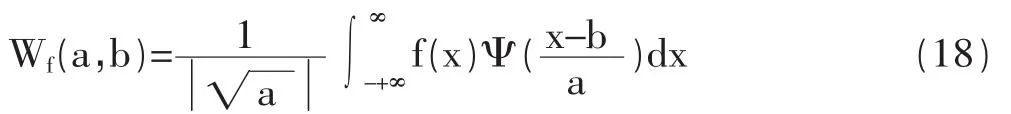
小波多分辨分析(Mu1ti-ResolutionAnalysis，MRA)是小波分析中最重要的概念之一，它从函数空间的高度研究函数的多分辨表示，将一个函数表示为一个低频成分与不同分辨率下的高频成分运用小波多分辨率分析方法对离散序列进行分解与重构，可将信号分解成低频成份 c1（t）和高频成份 d1（t），再将低频成份 c1（t）进一步分解,如此复就可得到任意尺度上的高频成份和低频成份。算法为

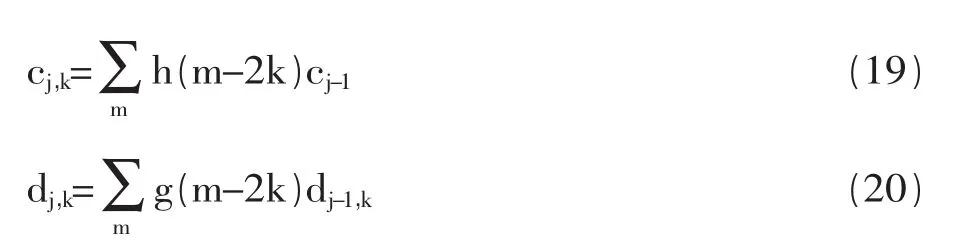
式中 k，m 为平移系数；cj，k为低频系数；dj，k为高频系数；，h（m-2k），g（m-2k）分别为低通滤波器和高通滤波器。利用分解后的小波系数可以重构原始序列，小波系数的重构形式可表示为下式：

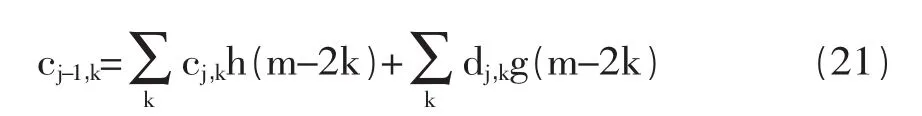
3.小波-BP神经网络（Wavelet-BP）

小波-神经网络从结构形式上看，可以看成是小波变换与常规神经网络的结合，其结构如图2所示，它是以小波分析作为神经网络的前置处理手段，为神经网络提供特征向量。即信号经小波变换后，再输入给BP神经网络完成分类及函数逼近功能[9]。

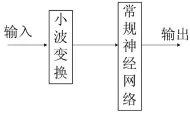
图2 松散型小波神经网络

4.风速预测

本文采用某风电场实测风速数据对所提方法进行验证。将获得的风速历史数据进行采用近似对称、光滑的紧支撑双正交小波db4作为母小波，对风速原始序列a0进行二尺度分解，获得该序列的基础分量a2，和细节分量d1、d2。在基础分量和各高频细节分量中分别提取200个训练样本对和80个测试样本对，并做归一化处理[10]。

对经小波分解得到的三个风速分量分别建立BP网络模型，采用数据滚动方法对模型进行训练和预测，然后将各分量的预测结果通过小波重构算法得到原始风速的最终预测值，仿真结果如图3。

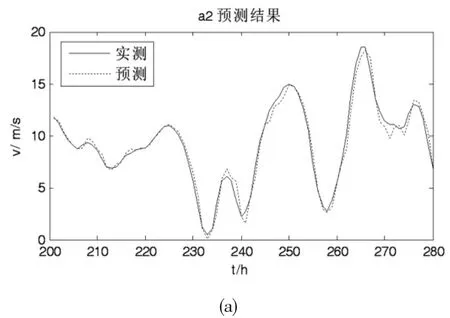
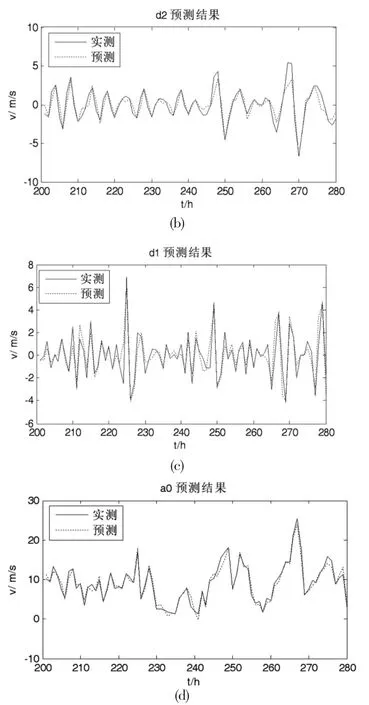
图3 Wavelet-BP法预测结果

图3分别给出了基础分量和细节分量、预测曲线，（d）是经系数重构后原始风速序列的预测曲线。图4是直接采BP神经网络的风速预测结果。可见将小波分解技术作与神经网络相结合的预测方法比单纯的BP网络预测精度要高，这是因为小波分解预测模型提取了反映风速变化的规律，降低了随机成分对确定性成分的干扰，从而提高了预测精度。

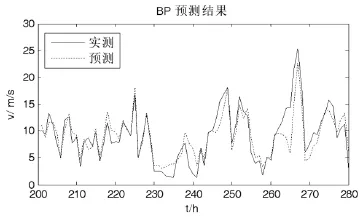
图4 BP法预测结果

4.结论

风速时间序列的变化过程具有连续频谱的特性。针对这一特征，本文提出了基于小波分析和神经网络的风速预测方法，通过小波变换，将各序列分量分别投影到不同的尺度上，并对不同风速分量分别采用相应的BP神经网络模型进行预测。最后通过小波重构，得到完整的风速预测结果。通过对实际预测结果的分析与评价表明，新方法具有较高的预测精度。

[1]肖永山，王维庆，霍晓萍.基于神经网络的风电场风速时间序列预测研究[J].节能技术，2007，25（2）：106-108.

[2]丁明，张立军，吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备，2005，25(8)：32-34.

[3]杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究[J].中国机电工程学报,2005,25(11):1－5.

[4]潘迪夫,刘辉,李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008,28(26):87-91.

[5]杜颖，卢继平，李青，邓颖玲.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(15):62-66.

[6]彭玉华.小波变换与工程应用[M].北京：科学出版社，1999.

[7]张彦宁,康龙云,周世琼,曹秉刚.小波分析应用于风力发电预测控制系统中的风速预测[J].太阳能学报,2008,29(5):520-524.

[8]肖永山，王维庆，霍晓萍.基于神经网络的风电场风速时间序列预测研究[J].节能技术，2007，25(2)：106-108.

[9]田景文，高美娟.人工神经网络算法研究及应用[M].北京：北京理工大学出版社，2006.

[10]储茂得，周松林.基于小波分析与神经网络的风电场短期风速预测[J].安徽科技学院学报，2011，25(1)：35－38.