预测反褶积在压制周期性多次反射波中的应用研究

唐海敏 苗庆库 王 银

(铁道第三勘察设计院集团有限公司，天津 300251)

反褶积也叫反滤波，在反射地震资料处理中已经作为最常用的技术之一。它是通过压缩基本地震子波以提高地震资料时间分辨率的过程。反褶积一般用于叠前，也广泛用于叠后资料。反褶积产生更高时间分辨率的剖面，没有反褶积的叠加剖面上的鸣震性质，即地震波经多次反射形成的干扰，显著地限制了分辨率。预测褶积的理论用于解决反褶积的问题叫做预测反褶积，它既可以用于压制海上资料虚反射之类的多次波，又可用于陆上压制地震信号的层间多次波，现在已经是一种常规的处理步骤。

1969年4月号地球物理杂志发表的Peacock和Treitel的文章中［3］描述了拟定削弱多次波(特别是海上常常遇到的鸣震)的长周期预测反褶积算子的方法。他们描述的预测反褶积算子设计方法致力于保留一次波，而尽力削弱多次波，其程序中的算子是针对削弱一次反射波后一定时间间隔有规则重复出现的周期性多次波而设计的。

本文通过对包含多次反射波的合成地震记录和Tesseral建模地震记录做多道预测反褶积，并尝试使用不同的预测参数(预测步长和预测算子长度)，通过反复对比，取得了较为理想的压制多次波效果。

1 预测反褶积原理

所谓反褶积是一个滤波过程，在地震勘探中这个滤波过程的作用恰好与大地滤波的作用相反，如图1所示。

图1 大地滤波和反褶积的流程对比

地震勘探的基本原理是向地下输入一个短信号，该信号可从地下两个地层单元的界面上反射回来。在此类模型中，脉冲函数并不是简单的速度差而是波阻抗差。由此得出众所周知的反射系数基本公式

式中，ρ是密度，v是波速。

地震道X(t)是由有效波s(t)和干扰波n(t)叠加组成的，具体公式如下

该有效波是一次反射波，对反射地震勘探而言，除一次反射波以外的波一般可视为干扰波。层状介质的一次反射波通常用线性褶积模型表示。

褶积模型公式

式中，w(t)为系统子波，r(t)为反射系数函数，n(t)为干扰波。

一道合成地震记录是震源子波w(t)与一个反射率模型r(t)相褶积的结果。

预测反褶积是用预测的方法，根据地震记录一次反射和干扰的信息预测出纯干扰部分，再从包括一次波和干扰的地震记录中减去纯干扰部分，以压制一次反射后面的多次波干扰，得到压制后的一次反射信号。在预测反滤波问题中，设计一个预测因子c(t)，对输入地震记录x(t)的过去值x(t－m)，x(t－m+1)，…，x(t－1)和现在值x(t)进行预测，所得到的未来的预测值x(t+a)是海上鸣震或陆地多次波干扰，将它从包括一次反射和干扰的地震记录x(t+a)中减去，所得到的预测误差ε(t+a)=x(t+a)－x(t+a)就是压制干扰后的一次反射信号。

1.1 多道多步预测误差滤波器

设有K道地震数据，每道时间采样为M+1，预测步长为L，多步预测滤波器系数个数为N，

则多步向前预测误差定义为

CN，j是K道多步向前预测误差滤波器的K*K阶(1≤K≤K)矩阵系数。

可以整理为矩阵表达形式

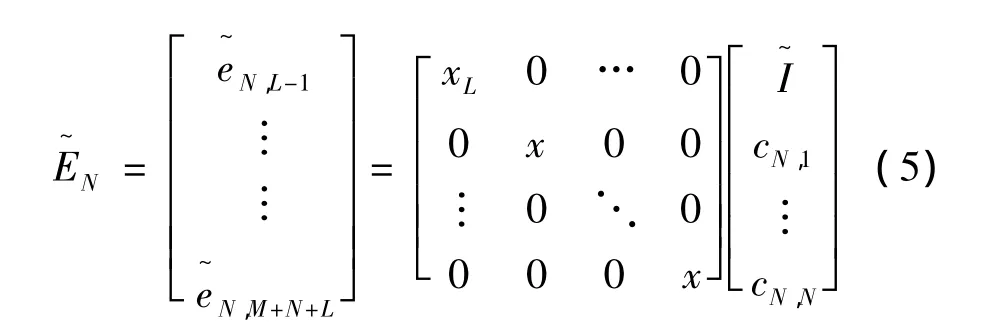
I是K阶的特征矩阵。

将预测误差的平方和最小化得到扩展的多步向前预测误差滤波常态方程

R0是 K*K 阶，RL+i－1，i=1，…，N 是 K*K 阶，R－L－i+1

PN是最小向前多步预测误差协方差矩阵

1.2 预测滤波器的算子长度和预测步长

维纳推导出将输入转换为任意期望输出的滤波器。

一个长度为n的矩阵方程的普遍形式是［8］

式中，ri，ai，及 gi(i=0，1，2，3，…，n －1)分别是输入子波自相关，期望滤波系数及期望输出与输入子波的自相关。

最佳维纳滤波器ai是最佳的，是指它的实际输出与期望输出之间的最小平方误差最小。当期望输出是零延迟尖脉冲(1，0，0…0)时，维纳滤波就与最小平方滤波等同。换句话说，后者是前者的特例。

给定输入X(t)，我们需要预测它在某一将来(t+α)的值，这里α是预测步长。维纳指出，用于估计X(t+α)的滤波器可用如方程(8)的一个矩阵方程的特殊形式来计算［8］。

方程(8)可一般化为一个长度为n的预测滤波器及一个预测步长为α的情况

现在考虑单位预测步长，α=1，n=6的特殊情况，则方程(9)可改写如下

式中，L=r0－r1a0－r2a1－r3a2－r4a3－r5a4

尖脉冲反褶积实际上是单位预测步长预测滤波器的特殊情况。

合成资料的例子展示了多道预测反褶积在削弱在资料中周期性出现的多次反射的有效性。

2 合成地震资料的预测反褶积

设计一个合成地震记录，该记录有10道，每道有1000个采样点，采样时间1 s，共产生三次多重反射波，分别在400 ms，600 ms，800 ms，多次反射波的周期为200 ms，设反射系数c=－0.333，加入随机噪声为+/－0.001，

合成地震记录如图2所示。

图2 合成地震记录

反褶积后如图3所示。

使用的参数为:反褶积一道所用的道数=5，预测步长=200 ms，多重反射周期=200 ms。

图3 反褶积后的合成地震记录

3 Tesseral模型设计及预测反褶积对比研究

新建模型如图4所示，有两个水平层，上层为海水，下层为某岩层，横向宽度为1000m，纵向深度为1000m，炮点放在中间500m处，检波器范围从600m到1000m，道间距取4m，炮点距离最近的检波器长度为100m，地震信号记录时间从0 s开始到2 s结束，采样间隔为2 ms，每道有1000个采样点。

子波设为70 Hz最小相位子波，经计算该子波的波长约为21 ms，试验中预测步长L不能小于21 ms，否则将造成子波的畸变。

第一层:纵波波速1 500m/s，横波波速0.25m/s，密度1 g/cm3;

第二层:纵波波速2 500m/s，横波波速1 450m/s，密度2.2 g/cm3。

根据反射系数计算公式，可得反射系数c=(2 500×2.2－1 500×1)/(2 500×2.2+1 500×1)=0.571 4。

在波阻抗相差较大的情况下，比较容易产生多次反射波。

图4 多次波形成的地质模型

以下是一个多次反射模型的示意，O为震源，R，M1，M2，M3为检波器位置，如图5所示。

图5 全程多次反射波形成示意

选择弹性波模拟，生成的原始含有多次反射波的地震单炮记录，如图6所示。

图6 含多次反射波的地震单炮记录

在程序中涉及到三个参数:

①反褶积一道所使用的相邻道数nc;

②预测算子长度ncf;

③预测步长L。

多次波周期可以近似为(200×2)/1 500=267 ms，归一化后相当于P=135。先固定两个参数nc=5，L=135，取预测算子长度 ncf分别为 30 ms，50 ms，80 ms，100 ms，150 ms，200 ms，可对比得出 150 ms 和 200 ms的预测算子长度后的结果都很好。为了提高计算效率，选定ncf=150 ms为好。

固定nc=5，预测算子长度选择ncf=150 ms，因为再增大算子长度，反褶积的效果保持稳定不变，而大的算子长度会占用比较多的计算时间，影响运行效率。综合考虑算子长度选择150 ms，取预测步长分别为L=8 ms，50 ms，100 ms，110 ms，120 ms，130 ms，160 ms，200 ms，280 ms。

步长的选择出现两端差中间好的现象，即预测步长太小会出现很多噪声和不规则的扰动，步长太大则压制多次波的效果不好。经比较，预测步长选择120比较适宜。

单独考虑nc的选择，即反褶积一道所用的相邻道数，固定好其他两个参数，预测算子长度ncf=150，预测步长固定为L=120，取nc=5和10做对比，二者几乎没有任何效果上的差别，如果选nc=10，计算时间过长，效率低，综合考虑应该选取nc=5。

综上可知，对于本次试验，多道预测反褶积压制周期性地震多次波干扰的三个参数最佳值应是:

反褶积一道选取相邻道数nc=5;预测算子长度ncf=150 ms;预测步长L=120 ms

4 结论

关于预测反褶积的参数选择，预测步长以取最远道的自相关极值为佳，并通过试验确定最佳预测步长。预测算子长度应该大于多次波的周期长度，如果算子长度取小了，就会使预测结果带进假的能量，使预测反褶积波形尾部出现波动，但算子长度也不能太大，长度太大不仅增加计算量，而且会增加相邻反射及噪声的影响。预测反褶积程序的执行效率较高，宜通过对比试验综合确定最佳参数。

［1］［美］渥．伊尔马滋．地震数据处理［M］．黄绪德，译．北京:石油工业出版社，1994:71-135．

［2］大港油田科技丛书编委会．地震勘探资料处理和解释技术［M］．北京:石油工业出版社，1999

［3］Peacock K L， Treitel S．Predictive deconvolution Theory and practices．Geophysics，1969，34(2):155-169

［4］陆邦干，范伟粹．地球物理资料数字处理［M］．北京:石油工业出版社，1987:80-102

［5］黄绪德．反褶积与地震道反演［M］．北京:石油工业出版社，1992:1-10，45-69

［6］N．S．奈德尔，等．褶积模型［M］．牛毓荃，译．北京:石油工业出版社，1986．:51-54，126-165

［7］牟永光．地震数据处理方法［M］．北京:石油工业出版社，2007:80-90

［8］Robinson，E．A．，and Treitel，S．．Geophysical signal and analysis．Prentice-Hall，Inc．1980