光滑粒子流体动力学的一种并行数值计算方案

周 浩，汤文辉，冉宪文，陈 华

（国防科学技术大学 理学院 工程物理研究所，长沙 410073）

0 引言

随着航天科技的迅速发展以及航天发射任务的急剧增加，大量的空间碎片散布在近地轨道上，形成了复杂的空间碎片环境，对航天器的安全构成了极大的威胁。如何确保航天器的飞行安全，成为当前航天器设计中一个十分重要的问题。对超高速碰撞问题进行理论研究非常困难，而现有的试验技术又很难达到超高速碰撞所需要的速度条件，因此数值模拟是一种重要的研究手段。有限元方法作为当前计算力学领域主要的数值计算方法，经过多年的发展，日渐成熟和完善，被广泛应用于解决工程问题。但是在面对超高速碰撞等涉及到大变形的问题时，应用有限元方法经常会产生网格畸变，严重影响计算精度，甚至导致计算终止。

光滑粒子流体动力学（smoothed particle hydrodynamics，简称SPH）方法[1-3]是近年来比较热门的一种无网格流体动力学算法，它既保留了拉氏计算描述物质界面准确的优势，又具备欧拉方法的长处，而且逻辑简单，统一地处理不同维数的问题，能够避免有限元方法中的网格缠绕和扭曲等问题，因而特别适合计算多物质的大变形问题。在SPH方法中，物质被离散为一系列“粒子”，每个粒子携带如密度、压力、速度、内能等属性，通过质量、动量、能量三个守恒方程，利用附近粒子相应物理量插值得到各个粒子物理量的随体导数，使拉氏流体力学偏微分方程组变成差分方程组，从而易于数值求解。SPH中的一个主要问题是计算量比较大，耗时较长，所以开展并行计算研究十分必要。

1 SPH方法并行计算方案

并行编程比较复杂，面临着执行结果的不确定、如何在各个进程间合理地划分任务、如何减少通信，以及对于不同进程数（即不同数量的核）具有伸缩性等问题[4-6]。本文从实际需要出发，采用基于MPI（Message Passing Interface）的信息传递并行程序设计平台和粒子分割算法。每个进程中都有array1和array2两个数组，分别用来存储所有粒子信息和所有粒子随体导数信息。在信息处理中，只需维护每个进程中互不重叠的一部分信息。虽然这样处理每个进程会降低程序编写复杂度（特别是在递归搜索粒子对以及计算各个粒子随体导数时），但仍存在一些冗余信息。

1.1 近邻粒子搜索的并行方案

SPH计算最耗时的部分是近邻粒子搜索，而并行的 SPH方法对近邻粒子采用了并行搜索算法，可有效减少计算时间。目前主要的并行搜索算法有全配对搜索、链表搜索和树搜索3种，其中：全配对搜索算法最简单直接，但是计算量为 N2，只适合于极少数粒子的情况；链表搜索算法效率比较高，但是对于可变光滑长度缺乏自适应能力；而树搜索算法效率相对较高，且对于可变光滑长度具有良好的自适应能力。因此，本文采用了树搜索算法。

近邻粒子树搜索算法是 Hernquist和 Katz于1989年在TreeSPH方法研究中提出来的。它首先通过递归的方法构造一棵树，树的每个节点代表一块空间。树的根节点代表整个计算空间，子节点代表父节点空间的子空间。如果某个子节点包含的粒子数大于1，则继续划分此节点，直到所有子节点只包含一个粒子。对于任意粒子i，以两倍的光滑长度为边长构造一个立方体，使i粒子位于立方体的中心。检验该立方体与树的根节点所代表的空间是否有重合，如果有，则遍历此树节点的所有子节点，直到当前树节点所代表的空间处仅有一个粒子为止。然后判断该粒子是否在粒子i的影响域内，如果是，则该粒子为i粒子的近邻粒子；如果不是，则停止在此节点及其所有子节点的搜索。对于二维情况，树搜索算法如图1所示[7]。

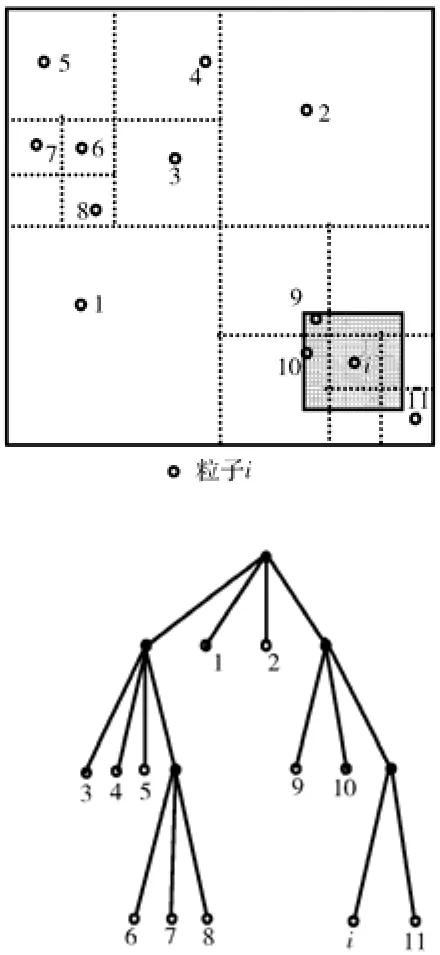
图1 树搜索算法示意图Fig. 1 Tree search algorithm in two-dimensional space

假设参与计算的进程总数为np且为奇数，于是令np=2m+1。首先把所有粒子大概平均分为np组，每个进程维护一组粒子。设第i组和第j组之间的邻域粒子对表示为(i, j)，其中 i=1, 2, ……, np，j=i,i+1, ……, np，于是所有的邻域粒子对被分成了np(np+1)/2类，即将一个大任务分成为np(np+1)/2个小任务，而每个进程将承担(np+1)/2=m+1个小任务。

为了简便，下面以np=5为例展开讨论。此时，所有邻域粒子对被分为如下 15类：(1, 1)、(1,2)、……、(1, 5)，(2, 2)、……、(2, 5)，(3, 3)、……、(3, 5)、……、(5, 5)。每个进程承担3类，各个子任务在每个进程上面的分配如表1所示。

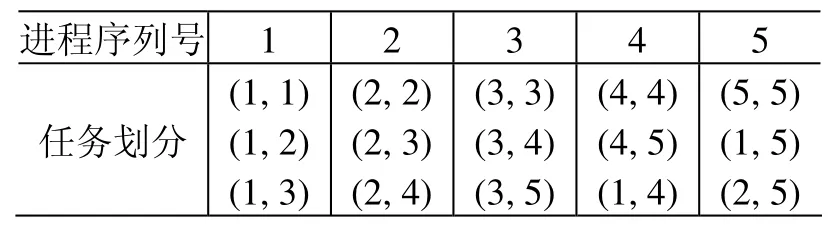
表1 在5个进程上的任务划分Table 1 Task partition of five processors

在进程1上用第1组粒子造一棵树，则第1、2、3组粒子在这棵树上搜索，找到近邻粒子对(1,1)、(1, 2)、(1, 3)；在进程2上用第2组粒子造一棵树，则第2、3、4组粒子在这棵树上搜索，找到近邻粒子对(2, 2)、(2, 3)、(2, 4)；……；在进程5上用第5组粒子造一棵树，第5、1、2组粒子在这棵树上搜索，找到近邻粒子对(5, 5)、(1, 5)、(2, 5)。由此可以看到：在每个进程上用某组粒子构造一棵树时需要3组粒子的信息，而在一步搜索中需在这棵树上搜索3组粒子。

在搜索的同时，每个进程上如果发现粒子i、j是近邻粒子，那么立刻计算有关i、j粒子的核函数及其导数，并且在array2(i)和array2(j)上面各加上一项。这样，进程1就计算了第1、2、3组粒子随体导数的部分信息，进程2计算了第2、3、4组粒子随体导数的部分信息，……，进程5计算了第5、1、2组粒子随体导数的部分信息，如此处理就不需要一个超大数组来存储所有粒子对信息。

1.2 每一次循环的计算步骤

在循环之前先建立2m+1个通信子，每个通信子包含的进程对应于表2中每行的所有进程，如通信子1包含进程1、m+2、m+3、……、2m+1，通信子 2包含进程 2、m+3、m+4、……、2m+1、1等等。计算中每一次循环包括以下四个步骤。

第一步：粒子信息交换。对于np=5的情形（如表1所示），进程1上面存储了第1组信息，而进程4、5为了维护第4、5组粒子信息，需要知道第1组粒子信息，所以进程1需要将第1组粒子信息传递给进程4和5。同理，进程5需要将第5组粒子信息传递给进程3和4。这一步信息流动方向如表2所示。

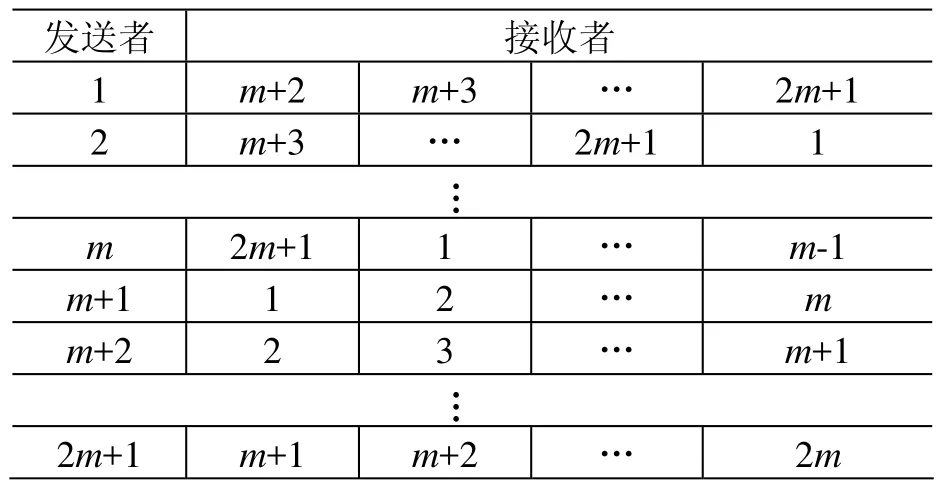
表2 第一步中的信息流动方向Table 2 Information flow in step one

可以看出，这一步中只需要每个进程在循环之前创建的通信子中调用若干次广播函数。

第二步：粒子搜索与随体导数更新。每个进程用自己维护的那部分粒子造一棵树，然后找到所有分配给自己的粒子对，并更新相应粒子的随体导数。对应于表1，进程1用第1组粒子造一棵树，找出粒子对(1, 1)、(1, 2)、(1, 3)并更新第1、2、3组粒子的随体导数；……；进程5用第5组粒子造一棵树，找出粒子对(5, 5)、(5, 1)、(5, 2)并更新第5、1、2组粒子的随体导数。每一次搜索完成之后要编一个递归子程序销毁之前造的树，否则计算一段时间之后会因为虚拟内存不足而导致计算停止。这一步是 SPH并行计算的主要步骤，占了整个计算时间的绝大部分。

第三步：交换粒子随体导数信息。对应于表1，进程4和5有部分关于第1组粒子随体导数的信息需要传递给进程1，进程5和1有部分关于第2组粒子随体导数的信息需要传递给进程2等等。这一步的信息流动方向与第一步刚好相反，所以只需要每个进程在循环之前创建的通信子中调用若干次求和归约函数。这一步结束后，每个进程就在array2中相应位置保存了自己维护的那部分粒子的随体导数。

第四步：每个进程利用粒子随体导数信息和时间步长更新自己维护的那部分粒子的信息。

为了测试以上4步的时间消耗情况，我们设置了1 825 600个粒子，分别申请不同数量的进程，得到的结果如图2所示。

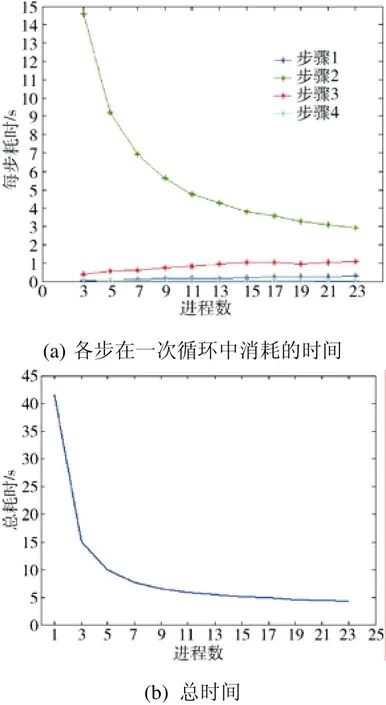
图2 不同进程数的时间消耗对比Fig. 2 Running time with different numbers of processors

图2(a)中，第1、3步属于通信，运算时间随着进程数的增加而增加；而第2、4步属于计算，运算时间随着进程数的增加而减少。

图2(b)表示对于大约182万个粒子，在23个进程内，计算时间随着进程数的增加而减少。在用23个核并行计算时，一次循环中4步计算加起来总共需要4.34 s，而在“银河”机上串行计算需要41.5 s，所以加速比为9.56，并行效率为41.57%。但是如果进程数继续增加到一定数量，则粒度将继续减小，通信时间的增加将超过每个进程上因任务减少而减少的计算时间，因而计算时间将增加。于是对于任意固定的粒子数，总是存在一个最优的进程数。由于权限之故，本文只考虑了进程数在 24个以内的情况。

2 计算实例

实例为圆柱形锌弹丸正面碰撞锌板。弹丸直径为3.98 mm，长14.15 mm；锌板厚0.965 mm；粒子之间的初始距离为0.1 mm，弹丸设置176 080个粒子，靶板设置1 243 770个粒子，总粒子数为1 419 850；弹丸速度为4.97 km/s。在“银河”5万亿次计算机上申请23个核并行计算。采取变时间步长，模拟10.5 µs需要3 160步，耗时3.25 h；而串行计算则需要36.7 h，因此加速比大约为11.3，并行效率为49.1%。试验结果[8]与计算结果对比如图3所示。

图3 锌杆弹丸撞击锌板试验与模拟对比Fig. 3 Comparison between the experiment and calculation for the impact of zinc rod on zinc slab (10.5 µs after impact )

由图3可以看到，计算结果和试验结果基本吻合。试验测量的碎片云长度为55.4 mm，而计算结果为55.1 mm。

第二个例子为铜盘正面碰撞铝板。铜盘弹丸重3 g，其速度为5.55 km/s；直径11.18 mm，厚3.45 mm，设置343 105个粒子。铝板厚为2.87 mm，设置2 562 005个粒子。模拟6.4 µs需要1 737步，耗时3.95 h；而串行计算则需47.1 h，因此加速比约为11.9，并行效率为51.8%。试验结果[8]与计算结果对比如图4所示。

图4 铜盘撞击铝板试验与模拟对比Fig. 4 Comparison between the test and calculation for copper disk impacting on aluminum plane(6.4 µs after impact)

由图4可以看到，碎片云的计算结果和试验结果基本吻合。

3 结束语

SPH方法计算三维超高速碰撞很有优势，但运算量很大。针对这个情况，我们设计了一种并行计算方案并且实现了数值模拟。这种方案简单直接，易于编程，整个并行三维SPH程序只有1 000多行，而且和并行相关的只有主程序中的200多行，从几万到几百万个粒子规模以内能够提供大约10的加速比，即并行计算时间为串行计算的1/10，显著减少了SPH方法的计算时间。

（References）

[1]Liu G R, Liu M B. Smoothed particle hydrodynamics[M].Singapore: World Scientific, 2003

[2]Monaghan J J. Particle methods for hydrodynamics[J].Computer Physics Report, 1985(3): 71-124

[3]李宝宝. 超高速碰撞下相变效应的数值模拟研究[D].长沙: 国防科学技术大学硕士学位论文, 2010

[4]陈国良. 并行计算——结构、算法、编程[M]. 北京: 高等教育出版社, 2003

[5]都志辉. 高性能计算之并行编程技术——MPI并行程序设计[M]. 北京: 清华大学出版社, 2001

[6]张武生, 薛魏, 李建江, 等. MPI并行程序设计实例教程[M]. 北京: 清华大学出版社, 2009

[7]徐金中. 空间碎片超高速碰撞特性及其防护结构优化设计的SPH研究[D]. 长沙: 国防科学技术大学博士学位论文, 2008

[8]Mullin S A, Littlefield D L, Anderson C E, et al. An examination of velocity scaling[J]. Ibid, 1995, 17:571-581