制动闸片结构特征的表征方法研究＊

孙 超，高 飞，符 蓉，农万华

（大连交通大学 连续挤压教育部工程研究中心，辽宁大连116028）

盘形制动是现阶段高速列车广泛使用的一种制动方式，它利用闸片和制动盘的摩擦将动能转化为热能，再通过热交换的方式将热量散发出去。由于高速列车制动过程中产生的热负荷相当大，因此，制动盘处于强烈的热应力环境条件下，从而导致热疲劳［1-2］失效成为制约制动盘寿命的主要原因。影响制动盘热疲劳寿命的因素有很多，如材料性能［3-4］、制动盘结构［5］、表面压力分布、制动工况［6］、摩擦副的匹配型式等，在这些影响因素中，一个重要的因素是闸片的结构型式，闸片结构型式的不同，直接导致制动盘表面各点摩擦接触的时间不同，同时，结合各点的摩擦速度的差异，造成盘面各点的摩擦功及摩擦功率处于不均匀的分布状态，这均导致盘面温度场处于一个不均匀的分布状态，从而形成相当大的热应力，加剧了热疲劳程度。因此，研究闸片结构型式与制动盘温度场的关系是一个有意义的课题。实际应用中，各闸片制造企业根据企业的条件和技术水平，制造的闸片型式多种多样，评价这些闸片对制动盘温度场的影响，往往借助于数值模拟计算的方法，但这种方法的局限性在于模拟条件难于确切，而且需要相当长的计算时间。显然，如果通过闸片的几何结构参数，找到一种能评价闸片对制动盘温度场影响程度的特征值，将对设计高性能闸片和提高制动盘热疲劳寿命是有积极意义的。

从盘形制动闸片的结构差异与制动盘温度场及应力场的关系出发，针对摩擦块的形状为三角形、六边形、圆形的典型结构，运用摩擦功率与摩擦周向接触长度的关系，探讨制动闸片的表征方法，并通过有限元分析软件ABAQUS模拟计算进行了验证。

1 闸片结构的表征方式

图1 圆形、六连形、三角形排布的12种结构形式的闸片

图1是分别由圆形、六边形、三角形3种形状摩擦块组成的12种具有不同型式的闸片。可见，摩擦块的几何形状、排布方式的不同，可导致闸片表面积的分布型式有差异。闸片表面积及位置的差异，在摩擦中，对应盘面的位置不同，形成的摩擦区域有所差别，导致制动盘摩擦接触面积发生相应的变化，从而影响摩擦热在制动盘上的分布形态，形成不同的温度场。因此，摩擦块形状、排布方式与制动盘温度场特征密切相关。显然，闸片结构对盘面温度分布的影响，就是一个闸片结构表征方式的问题。闸片结构的表征在于能够建立摩擦块空间分布与摩擦热关系。

基于盘面各点的摩擦热依赖于摩擦接触面积、作用时间和作用速度的角度，考虑到制动盘的摩擦面是二维空间，因此，可从径向和周向两方向上研究摩擦块空间布局对制动盘温度的影响。

1.1 摩擦块的径向结构因子

制动中，在不考虑散热的情况下，假设摩擦产生的能量沿制动盘周向均匀分布，闸片与制动盘组成的摩擦副在制动过程中产生的热源相对于制动盘运动，所以进入制动盘的任意一微分弧块的热流密度应为进入制动盘总热量与微分弧块在制动盘扫过面积的比值，则作用于制动盘位置点为r处的热流密度［7］如下：

式中A为闸片总面积，m2；F为对闸片施加的压力，N；R为车轮半径，m；μ为制动盘与闸片的摩擦系数；ω为制动盘角速度，rad／s；η为流入制动盘的热效率；vt为列车制动速度，m／s。

如图2示意图所示，将制动盘的摩擦区域划分为n个半径不同的摩擦环，在任意摩擦环上具有不同的摩擦副有效摩擦面积。

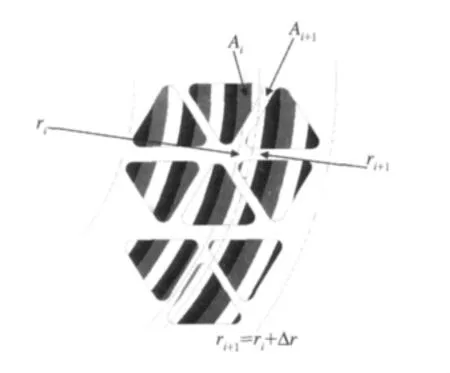
图2 盘面各摩擦环摩擦面积示意图

单位时间内通过半径为ri的任意摩擦环上的摩擦接触面积Ai的能量：

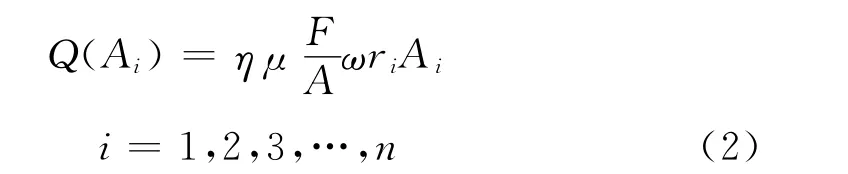
单位时间内整个接触面积上的总热量：

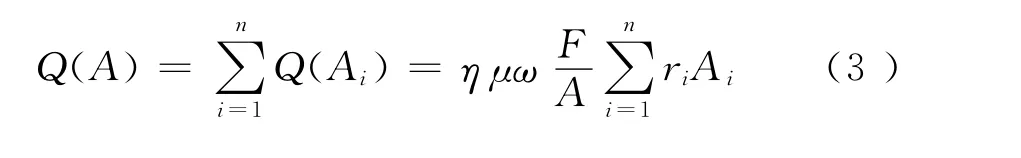
闸片在半径方向的分布差异反映在随半径不同，摩擦副的接触面积大小不同。从式（2）知，任意摩擦环上的热流密度与摩擦半径呈正比，而摩擦产生的热量与摩擦面积成正比，同样摩擦热与热流密度也成正比，所以，摩擦热与摩擦半径、摩擦面积呈正比关系。

由此可见，任意接触半径上单位时间内上所产生的能量占总能量的百分比将反映闸片的结构特点，这个比值可定义为径向结构因子fi：

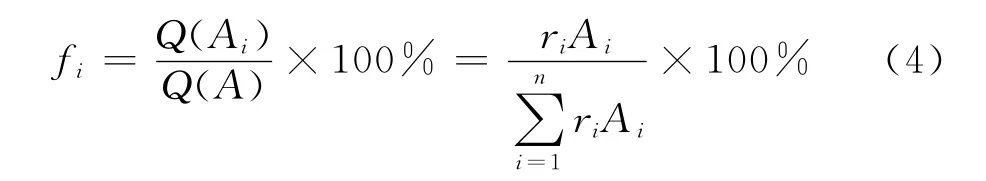
由（4）式可知，f与摩擦半径r及摩擦面积A均呈正比，因此，从能量分配的角度，f可以表征闸片结构径向分布的差异。任意摩擦环上的径向结构因子越大，此处产生的能量越多、温度越高。

基于公式（4），针对图1中3种形状摩擦块组成的12种结构的闸片，分别计算了其径向结构因子，计算结果如图3所示，可见，3种形状的闸片，随排列方式的不同，径向结构因子随半径变化均具有不同程度的波动，这个变化反映了摩擦块本身的几何形状、空间排列方式。由于径向结构因子分布直接反映了制动盘上的热量沿径向的分布，制动盘上最大结构因子位置对应热量最大位置。3种形状的摩擦块相比，圆形摩擦块的径向结构因子变化幅度略小。

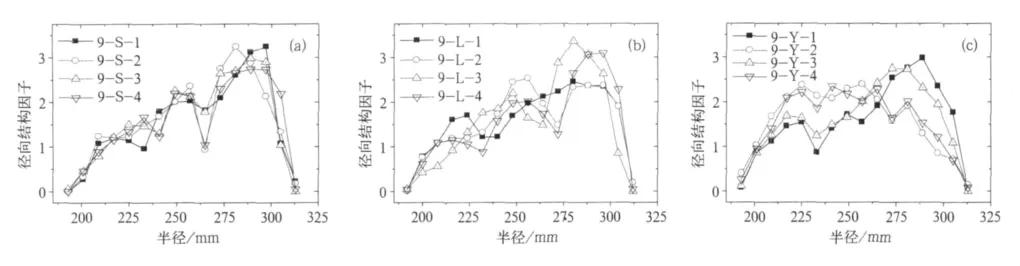
图3 结构因子与半径的关系

径向结构因子可以反映闸片摩擦块的排布和形状特征，但由于各曲线的波动性较复杂，直观很难判断波动性，因此，引入一个判断曲线波动性的波动系数Cmax。C为曲线波峰值与其波谷值之差与曲线所取点纵坐标之和平均值的比值。公式如下：

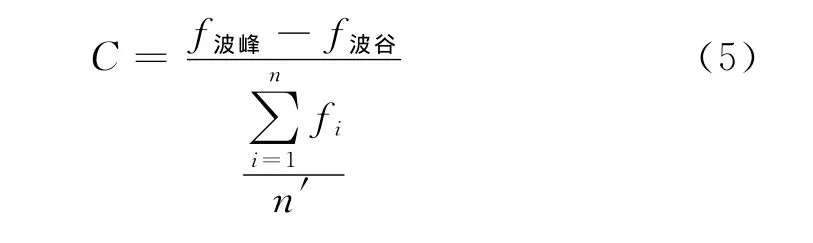
式中f波峰为曲线的波峰值；f波谷为曲线波峰相邻的波谷值，n′为曲线上所取点的个数；Cmax为计算出C值的最大值，Cmax可以表征曲线的波动性，其值越小，曲线的局部突变波动性越小。为判断各曲线的波动性，计算了各曲线的波动系数Cmax，具体数值如表1。

表1 径向结构因子曲线的波动系数Cmax

由表1数据可知，数量为9个的三角形、六边形、圆形摩擦块组成的12种方案中，S-3、S-4、L-2、Y-4的Cmax值，相对同形状闸片的其他排布方式，具有较小值。由此可判断，曲线的局部和整体波动性较小，摩擦块的排列方式比较合理。根据径向结构因子的物理意义，可以判定这几种闸片结构所对应的制动盘，其摩擦产生的热量分布较均匀。

1.2 摩擦块的周向结构因子

闸片的径向结构因子，可以反映闸片的结构对摩擦热沿径向的分布特点。同理，闸片的结构不同，也应该沿周向的分布上有所区别，这可通过周向结构因子来表征，其表达定义为在同一摩擦环上，摩擦块间空隙的面积S空与摩擦块摩擦接触面积的总和S总之比再乘以此摩擦环上摩擦块的个数n，即：

周向结构因子越大，闸片的径向分散程度越大。

图4是能反映周向结构因子的热源模型，基于这个模型，制动过程制动闸片和制动盘的关系，可看作为一个无限大平板与移动的面热源的关系。以一个无限大平板上具有3个总面积相等的面热源模型为例。热模型中散热系数不随温度变化是一个定值。热流密度定义为q，a中的面热源的面积为A0，b热源是有两个面积大小均为A1的面热源组成，其中A0=2A1，c热源由3个均匀分布的面积大小为A2的面热源组成，其中A0=3A2。分别可以代表大尺寸、中尺寸和小尺寸的摩擦块与制动盘组成的摩擦副，它们的周向分散度分别为：εa=0、εb=2／3、εc=1。

假设此3种面热源以一定的速度移动，则无限大平板的温度最大值应该出现在热源末端边界对称点上［8］。

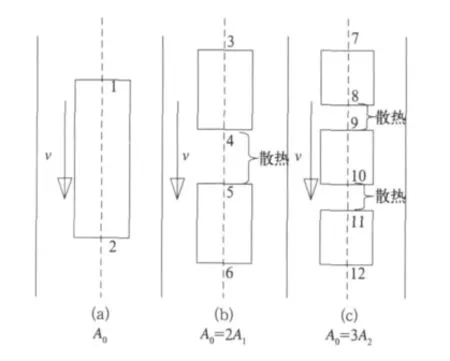
图4 无限大平板上的3个移动的面热源模型

热源由点1移动到点2过程中平板所吸收的能量：Qa=Q1→2

热源由点3移动到点6过程中平板所吸收的能量：Qb=Q3→4+Q4→5+Q5→6

热源由点7移动到点12过程中平板所吸收的能量：Qc=Q7→8+Q8→9+Q9→10+Q10→11+Q11→12

其中Q1→2=q·A0；Q3→4=q·A1；Q5→6=q·A1；Q7→8=q·A2；Q9→10=q·A2；Q11→12=q·A2；Q4→5＜0；Q8→9＜0；Q10→11＜0。

则：Qa=q·A0；Qb=Qa+Q4→5；Qc=Qa+Q8→9+Q10→11

可以推断：Qa＞Qb；Qa＞Qc。

由于热源引起的温度最大值与所吸收的能量呈正比关系，所以，由以上计算过程可以推测3个热源引起的温度最大值Tamax、Tbmax、Tcmax呈现以下关系：

由此可以推断，闸片的周向结构因子越大，制动盘表面最高温度越低。或者说，摩擦块尺寸越小，盘面最高温度越低。

2 摩擦块结构因子与制动盘温度分布的关系

2.1 数值模拟模型及模拟条件

图5是闸片与制动盘关系的数值模拟模型。模拟计算中，忽略散热的作用，模拟的速度为恒速80km／h、制动压力p=0.224MPa、制动时间5s，模拟采用有限元软件ABAQUS，模拟方法为摩擦副热力耦合［9］。以S-2、S-4、L-1、L-4及Y-1、Y-4闸片结构为模拟对象，计算闸片结构对制动盘温度场及应力场的影响。

图5 闸片与制动盘相互关系模型

2.2 计算结果与讨论

图6是模拟计算得到的6种结构闸片对偶盘表面的温度场分布结果。观察图6可见，6种闸片结构对应的制动盘表面的温度场均呈高低温带交替分布，形成3个高温带。但最高温度所在的高温带的位置略有不同，Y-2的最高温度位于制动盘的中部，其他闸片结构对应的制动盘的最高温度所在的高温带位于制动盘的外侧。由闸片的温度场分布可以直观的看出，最高温度带出现在摩擦接触面积最大的摩擦环上。

表2列出了最高温度摩擦环处的最高温度值、周向结构因子以及径向结构因子值。由数据可知，周向结构因子越大，制动表面最高温度越低；径向结构因子越大制动盘表面最高温度越高。此结论验证了以上对径向与周向结构因子的作用推测。

表2 最高温度摩擦环处的最高温度、周向结构因子、径向结构因子

图7为制动盘温度与径向结构因子沿制动盘半径方向的变化情况，可见，节点温度曲线与结构因子分布曲线均具有一定的一致性，均呈波浪式分布且存在3个波峰，波峰的位置基本一致，都处于摩擦接触面积最大的位置附近。说明制动盘的表面节点温度与结构因子沿半径方向具有相同的变化趋势，其两者存在对应关系。

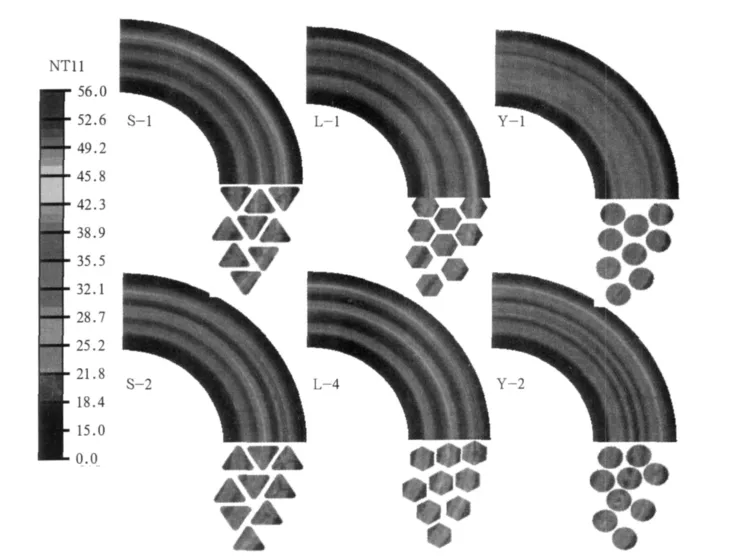
图6 制动盘与对应闸片的温度场分布

图7 节点温度及径向结构因子与半径的关系

由以上的分析可见，采用径向和周向结构因子表征闸片的结构是合理的；径向结构因子可以反映出制动盘的温度场分布；径向结构因子越大，盘面最高温度越高；周向结构因子越大，盘面最高温度越低。

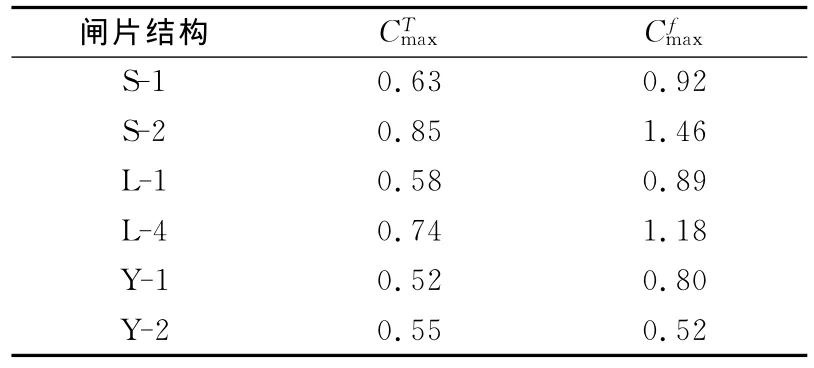
表3 温度曲线和径向结构因子曲线的波动系数Cmax

3 结论

（1）在闸片结构特征表征方面，引入了径向结构因子和周向结构因子的概念。径向结构因子反映了摩擦功率沿制动盘径向的分布规律；周向结构因子反映出摩擦功率在制动盘周向方面的分布规律，通过这两个参数，较客观地描述了闸片的结构特点，并可用于评价制动闸片对制动盘热应力分布的影响程度。

（2）径向结构因子随摩擦半径的增加，波动程度越小，盘面温度分布越均匀。周向结构因子越小，盘面的最高温度越低。这就要求在闸片设计中，尽可能使闸片周向弧长沿径向均匀分布，且每个摩擦块的尺寸小、数量多。这将有利于降低制动盘表面的最高温度，提高制动盘使用寿命。

［1］赵文清.高速列车“中华之星”制动盘温度场及热应力［J］.兵工学报，2006，27（1）：132-136.

［2］Gérard Degallaix，Philippe Dufrénoy，Jonathan Wong，et al.Failure Mechanisms of TGV Brake Discs［J］.Switzerland：ehavior of Materials X，2007，345-346：697-700.

［3］松宝韫，高 飞，陈吉光，于庆军，Yves.Berthier.高速列车制动盘材料的研究进展［J］.中国铁道科学，2004，25（4）：11-17.

［4］王文静，谢基龙，李 强，韩建民.铁路列车制动盘常用材料的热疲劳性能研究［J］.机械工程材料，2009，29（2）：40-41.

［5］Y.YILDIZ，M.DUZGUN.Stress analysis of ventilated brake discs using the finite element method［J］.International Journal of Automotive Technology.2010，133-13.

［6］顾磊磊，左建勇，朱剑月，吴萌岭.基于有限元法的动车组制动盘制动能力分析［J］.机车电传动，2009，（5）：7-9.

［7］罗继华，杨美传.动车组拖车制动盘有限元热分析［J］.铁道车辆，2009，47（4）：22-24.

［8］郑林庆.摩擦学原理［M］.北京：高等教育出版社，1994：253-255.

［9］王 皓.闸片结构对制动盘温度场及热应力场的影响［J］.铁道机车车辆，2010，30（4）：29-32.