基于预报偏差的LEO航天器轨道异常检测

张涛涛 白显宗 郝嘉 陈磊

（国防科学技术大学航天与材料工程学院，长沙410073）

1 引言

当航天器受到轨道机动、空间天气突变、解体或者极端情况下的碰撞等因素影响时，航天器的轨道会发生突变，此时，轨道异常事件检测信息可以为航天器所有者和操作者采取正确的措施提供依据。国内外学者针对航天器轨道异常问题，提出了多种检测方法。Patera提出了一种基于移动窗口曲线拟合 （Moving Window Curve Fit，MWCF）技术的空间事件检测方法，该方法在一定长度的时间窗口内对数据进行拟合，利用编目值和拟合值相减得到偏差，通过窗口的移动得到偏差数据序列，最后通过统计偏差数据的标准差设定检测门限进行异常检测［1］。Kelecy、Swartz等人基于Patera的曲线拟合技术对轨道异常检测方法进行了改进［2-3］。基于曲线拟合的检测方法存在移动窗口的长度和拟合曲线的阶次设定比较困难的不足。此外，董云峰等人提出了一种基于小波分析的轨道机动检测方法［4］。杨旭等人提出了单个卫星相邻根数时间差控制加综合判据的卫星轨道异常分析方法［5］。上述检测方法基本上从数据处理入手，利用数学方法直接分析轨道数据，不利于分析航天器轨道变化的物理规律。本文将航天器轨道预报与数学检测方法相结合进行航天器轨道异常的分析。

北美防空司令部（NORAD）发布的两行轨道要素（Two Line Elements，TLE）是目前最完整的空间目标编目数据，其对应的SGP4（Simplified General Perturbation 4）轨道预报模型是解析模型。作为例子，本文对航天器历史TLE数据进行分析，使用SGP4模型的长期项部分预报轨道根数的长期变化并基于马氏距离对航天器轨道异常进行判定。此外，本文所提出的方法同样适用于其他类型的轨道数据以及相应预报模型。

2 特征轨道要素长期变化预报模型

（1）特征轨道要素的选择

特征轨道要素是一个或多个可以表征航天器轨道异常的轨道要素或导出参数，选取合适的特征轨道要素是进行轨道异常检测的基础。航天器轨道异常主要可以分为两类：一类是轨道平面内轨道形状和大小发生突变，主要表现为半长轴、偏心率等参数的变化；另一类是轨道面的空间位置发生突变，主要表现在倾角、升交点赤经等参数的变化。为能够充分地表征这两类异常，本文选择轨道半长轴a和轨道倾角i作为特征轨道要素。

（2）基于SGP4模型的轨道要素长期变化预报

SGP4是一种考虑了地球非球形摄动、大气阻力摄动、第三体引力摄动等因素综合影响的轨道传播计算模型，其可以配合NORAD发布的TLE平根数进行航天器轨道预报［6-9］。

TLE数据包括空间目标的轨道要素以及其他相关信息，如目标编号、国际编号、大气阻力系数等。其中用于SGP4模型预报的参数包括：

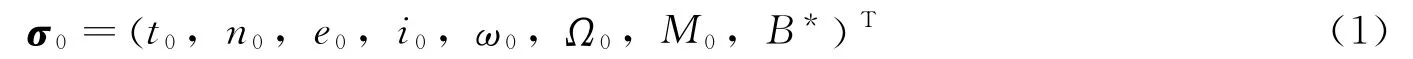
式中t0为历元时刻；n0为历元时刻的平均运动角速度 （转／天）；e0为历元时刻的平均轨道偏心率；i0为历元时刻的平均轨道倾角；ω0为历元时刻的平均近地点角距；Ω0为历元时刻的平均升交点赤经；M0为历元时刻的平均平近点角；B＊为大气阻力系数；这些轨道要素中的下标 “0”表示历元时刻的值。由TLE数据直接得到的n0是Kozai格式，需要转化为Brouwer格式平均角速度才可以使用SGP4模型进行轨道预报［9］：

对于LEO航天器，地球非球形摄动J2项对于半长轴的长期影响为零，同时由于其轨道高度较低，第三体引力、太阳光压等对半长轴的长期摄动可以忽略。影响LEO航天器半长轴长期变化的主要因素是大气阻力。尽管在这样的高度大气已经极为稀薄，但是由于航天器的飞行速度大、持续时间长，并且大气阻力不是保守力而是耗散力，因此航天器半长轴将缓慢减小。在大气阻力摄动影响下，半长轴长期变化可由下式描述［9］：

式中t-t0为预报时间间隔；C1，D2，D3，D4为相关的系数，详见参考文献［9］。

对于LEO航天器所处轨道中的非太阳同步轨道，其倾角受地球非球形摄动、大气阻力摄动、第三体引力摄动影响产生的长期变化量很小，可以近似为零。对于太阳同步轨道上的航天器，由于其轨道升交点赤经的进动角速度同地球公转角速度相同，太阳与轨道面的相对位置不变，因此太阳引力会导致轨道倾角的长期变化，可以表示为［10］

式中ns为地球绕太阳运动的平均角速度；n为航天器运动角速度；is为黄赤夹角；us为太阳在赤道上的平经度；Ω为航天器升交点赤经。

3 偏差数据生成

（1）轨道预报

轨道预报的基本方法如下：利用tk-1时刻的TLE编目轨道要素σk-1，通过SGP4模型长期项预报得到tk时刻轨道要素长期变化的预期值σk／（k-1），同时利用tk时刻的编目根数σk得到ak和ik，如图1。其中，下标“k／（k-1）”表示由tk-1历元时刻预报得到的tk历元时刻的预报值，下标“k”表示tk历元时刻的编目值。

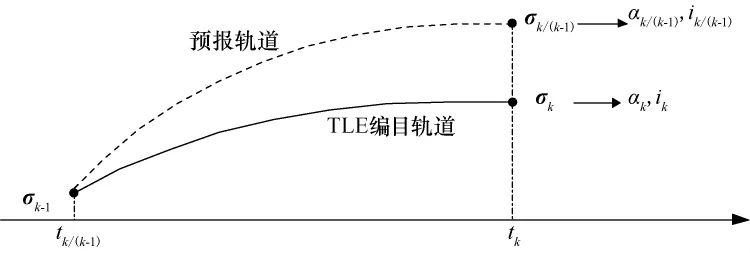
图1 基于SGP4长期项模型的轨道预报示意Fig.1 Orbit prediction based on SGP4model secular term

（2）数据平滑及偏差生成

TLE作为一种有效的空间目标编目数据，被广泛用于空间目标监视领域，例如航天器机动检测、碰撞交会分析、校核大气密度模型等［3］。由于测量、定轨以及模型精度 （例如地球模型、大气模型、预报模型）等因素影响，在得到的编目和预报数据中包含了一定的误差，上述误差会造成编目值和预报值在真值周围抖动，如图2。

图2 特征参数的抖动Fig.2 Dithering of characteristic parameters

这种抖动可能导致正常情况下偏差数据增大从而造成虚警，为了消除该小抖动并尽可能的保持原特征参数的变化，使用三次样条曲线对数据进行平滑处理。建立拟合目标函数如式（2），其中第一项代表拟合偏差，第二项代表拟合的平滑程度。

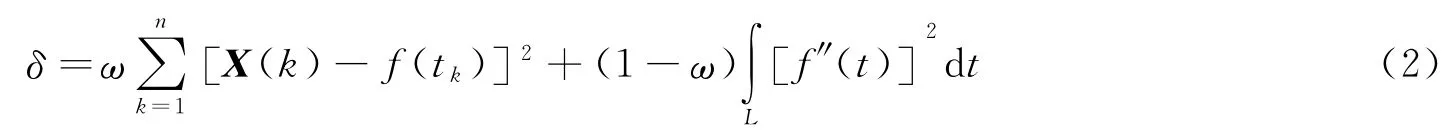
式中X为待平滑处理的数据序列；f为平滑得到的函数；L为所有历元时刻间隔中最小的时间段。

ω为决定数据拟合效果的权系数，取值范围为［0，1］。ω越大，拟合误差越小，但是拟合平滑效果越差；反之，ω越小，拟合得到的曲线越光滑，但是拟合偏差越大。为了在保持较小拟合误差的前提下获取较好的拟合效果，可以根据轨道情况的不同变化选取合适的ω，一般情况下，对于瞬时变化比较剧烈的情况，应该首要考虑控制拟合偏差，即选择较大的ω对于轨道参数变化较平缓的情况，可以适当的选择较小的ω，以便获得较好的拟合效果。本文中对二者进行了综合考虑，利用以下经验公式确定ω：

式中tj为第j个时间间隔；为所有历元时刻间隔的平均值。

依据目标函数，在Matlab中使用三次样条曲线对轨道半长轴和倾角的编目值和预报值进行平滑处理可得偏差数据序列：

式中

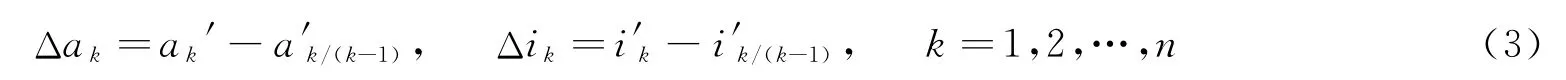
4 异常检测

偏差数据中包含半长轴和倾角两个参数，此时的检测可视为多维数据异常检测。在多维异常检测中，当各维分量代表不同质的量或者各分量的差异很大时 （如本方法中两个特征参数偏差量级相差较大），利用普通的欧氏距离计算会出现 “大数吃小数”的情况。马氏距离是对各维数据经过加权处理后描述两个数据点之间接近程度的量，可以有效避免该问题的发生。设总体均值为μ，协方差阵为Σ，ri为一个样本矢量，则样本ri到总体的马氏距离为［11］

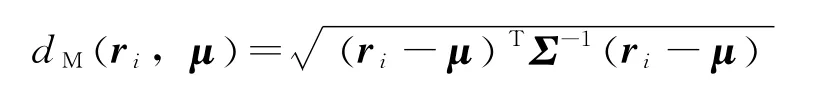
本文进行偏差数据异常分析时，总体的均值μ与协方差矩阵Σ均是未知的，可用它们的无偏估计即样本均值和样本协方差阵C代替，此时数据点ri到总体的马氏距离为

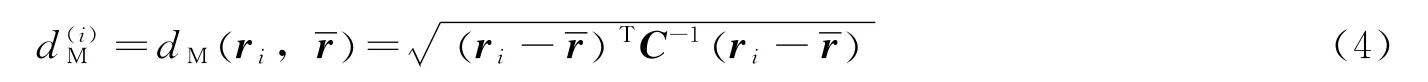
马氏距离实质上描述了考虑概率分布的数据点与分布中心偏离程度，样本值到总体的马氏距离越大表示产生此样本的概率越小，反之，马氏距离越小表示产生此样本的概率越大。

异常检测的偏差门限值dT可以依据检测精度选取，dT越大则误警率越低，但是漏警率越高；dT越小则漏警率越低，但是误警率越高。一般情况下可取为3～5。如果某样本值到总体的马氏距离大于给定的门限值dT，则认为该样本值为异常值。综上可得具体的算法流程如图3所示。

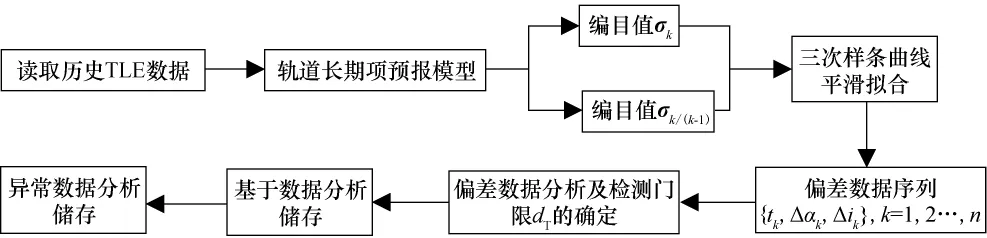
图3 基于预报偏差的轨道异常检测流程Fig.3 Flow chart of the detection method based on prediction dispersion

5 算例

Terra卫星是一颗美国的太阳同步轨道卫星，其装载的5种传感器能同时采集地球大气、陆地、海洋和太阳能量平衡的信息从而实现对地球的观测。下面以其为例，用本文所提出的方法进行轨道异常检测分析。表1为已知的Terra卫星2010年的轨道机动历史数据［12］。

表1 Terra卫星2010年轨道机动事件Tab.1 Maneuver history of Terra in 2010

对Terra卫星，利用NORAD发布的2010年的TLE数据［13］，进行分析可得到其2010年半长轴和倾角的变化情况如图4，图中竖线表示Terra卫星2010年的机动历史。

图4 Terra卫星2010年半长轴、倾角变化以及机动历史Fig.4 Semi-major axis，inclination history and recorded maneuvers of Terra in 2010

通过本文第3节所建立的轨道预报模型对Terra卫星的2010年轨道数据进行处理，可以得到其特征轨道要素的预报值，使用数据平滑处理方法对编目值和预报值进行处理可以得到平滑值。为便于说明问题，下面仅就Terra在2010年的第222天至228天之间的半长轴数据处理情况进行详细说明（见图5），轨道倾角的处理与此类似。

对Terra卫星的半长轴和轨道倾角进行预报、平滑处理后根据公式（3）可以得到其偏差数据，利用公式（4）可以得到每个历元时刻的马氏距离，并选取检测门限值为5对马氏距离数据进行异常分析，检测结果如图6和图7，图6中的①～⑥是检测到的6次轨道异常。

由计算结果可以看出，Terra卫星在2010年的异常值集中在6个时间点附近。分析原因可知：

1）轨道维持机动往往不是一次调整完成，而是在一段时间内不断的调整和测量达到设定值。

2）TLE定轨数据受到历史数据的影响，当发生轨道异常时不可能一次完成精确的定轨，而是利用多组新的轨道数据才能进行稳定的定轨。

综上可以判断Terra卫星在2010发生了6次轨道异常。检测结果的次数和时间均与已知的轨道机动历史相符。此外通过分析可知第1、3、4次为轨道高度维持，第2、5、6次为轨道倾角机动，而且其在倾角机动的同时对轨道高度进行了提升。

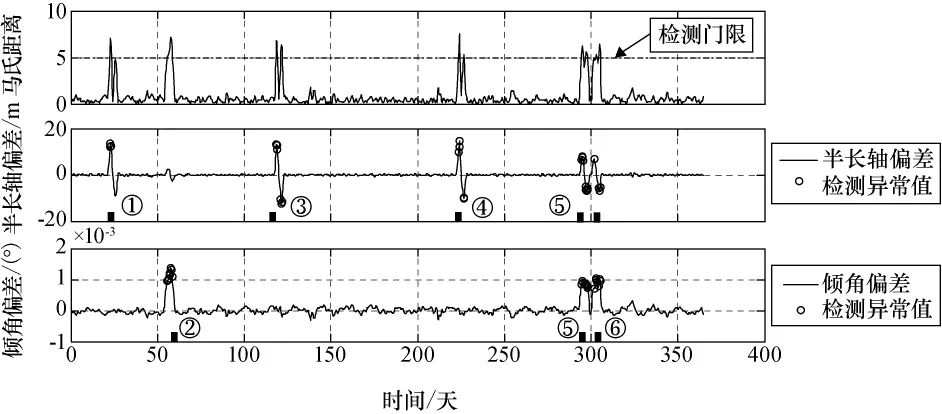
图6 Terra卫星2010年机动检测结果Fig.6 Maneuver detection results of Terra in 2010

图7 Terra卫星2010年半长轴、倾角偏差分布图Fig.7 Semi-major axis dispersion and inclination dispersion distributing of Terra in 2010

6 结束语

本文研究轨道异常检测问题，通过TLE数据分析了特征轨道要素的变化情况，在此基础上，利用轨道预报模型得到特征轨道要素的预报值，通过三次样条曲线拟合方法对编目值和预报值中的小扰动进行平滑处理后得到偏差数据，基于马氏距离对多维偏差数据进行异常检测，最后以Terra卫星2010年的机动事件检测为例进行了分析。

在以上研究的基础上，得出了如下结论：

1）本文所提出的方法能够确定轨道异常的次数、时间，选择轨道半长轴和轨道倾角作为特征轨道要素能够确定轨道的异常类型 （共面或异面）。

2）通过对TLE编目数据和预报数据进行平滑处理，可以有效地抑制了各种小扰动造成虚警。但是由于TLE数据本身精度和SGP4模型的预报精度有限，因此其不适合分析量级变化较小的机动，对于变化量级更小的轨道异常事件，使用更加精密的轨道预报模型和相应的数据进行检测将是下一步工作的重点。

［1］PATERA R P.Space event detection method ［J］.Journal of Spacecraft and Rockets，2008，45（3）：554-559.

［2］KELECY T，HALL D，HAMADA K，et al.Satellite maneuver detection using Two-line Element（TLE）data ［C］.Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference，Maui，Hawaii，September，2007.

［3］SWARTZ R L JR，COGGI J，et al.A Swift SIFT for Satellite Event Detection ［C］.AIAA／AAS Astrodynamic Specialist Conference，Toronto，Ontario Canada，August 2-5，2010.

［4］董云峰，苏建敏.利用小波分析识别空间目标的轨道机动 ［J］.宇航学报，2004，25（2）：213-218.DONG YUNFENG，SU JIANMIN.Detection of space target orbit maneuver by wavelet analysis ［J］.Journal of Astronautics，2004，25（2）：213-218.

［5］杨旭，刘静，吴相彬，等.利用TLE数据分析LEO卫星轨道异常的新方法——综合判据法 ［J］.空间科学学报，2011，31（2）：223-228.YANG XU，LIU JING，WU XIANGBIN，et al.New method to analyze the orbital abnormal of LEO satellite using TLE data——compositive criterion［J］.Chinese Journal of Space Science，2011，31（2）：223-228.

［6］HOOTS F R，ROEHRICH R L.Space Track Report No.3：Models for Propagation of NORAD Element sets［R］.Peterson：Aerospace Defense Command，United States Air Force，1980.

［7］VALLADO D A，CRAWFORD P，HUJSAK R，et al.Revisiting Spacetrack Report＃3 ［C］.AIAA／AAS Astrodynamics Specialist Conference and Exhibit，Keystone，Colorado，August 21-24，2006.

［8］VALLADO D A，CRAWFORD P.SGP4Orbit Determination ［C］.AIAA／AAS Astrodynamics Specialist Conference and Exhibit，Honolulu，Hawaii，August 18-21，2008.

［9］HOOTS F R，SCHUMACHER R W，GLOVER R A.History of analytical orbit modeling in the U.S.space surveillance system ［J］.Journal of Guidance，Control，and Dynamics，2004，27（2）：174-185.

［10］杨嘉墀.航天器轨道动力学与控制.［M］.北京：宇航出版社，2001.

［11］吴翊，李永乐，胡庆军.应用数理统计 ［M］.长沙：国防科技大学出版社，1995.

［12］UNITED STATES STRATEGIC COMMAND（USSTRATCOM）.Space-Track-Catalog Number Query Results.［EB／OL］.［2012-04-16］.http：∥www.space-track.org／perl／id＿query.pl.

［13］ATMOSPHERIC SCIENCE DATA CENTER.Terra Spacecraft Loss of Accurate Orbit Data Record［EB／OL］.［2012-04-16］.http：∥eosweb.larc.nasa.gov∥PRODOCS／misr／terra＿maneuvers.html.