基于人工免疫算法的地球-火星小推力转移轨道优化

彭坤 徐世杰 果琳丽 王平

（1中国空间技术研究院载人航天总体部，北京100094）（2北京航空航天大学宇航学院，北京100191）

1 引言

目前，小推力轨道的优化方法可分为间接法和直接法两大类。对于间接法，文献［1］中应用主矢量理论求解最优推力方向；文献［2］中分别用多点打靶法和最小边界条件法求解了近地小推力轨道优化问题。文献［3］中用多重打靶软件BNDSCO求解了多种燃料最省的小推力地火转移轨道。但间接法对初值敏感，难以收敛。直接法的初值均有物理意义，容易猜测，同时其通用性强。直接法的不足是寻优结果的最优性不能严格保证；寻优精度越高，计算量越大。在直接法研究中，文献［4］通过直接转录法求解最省燃料的地月小推力转移轨道。文献［5］中用序列二次规划（Sequential Quadric Programming，SQP）方法求解了地球到火星的燃料最省小推力转移轨道。但是SQP会遇到病态梯度、初始点敏感和局部收敛问题。文献［6］中利用退火遗传算法求解了定常推力地球-木星小推力轨道转移问题，有效避免了病态梯度、初始点敏感问题，但遗传算法本身容易陷入早熟收敛。

本文依据直接法的思想，将小推力轨道优化问题转化为非线性规划（Nonlinear Programming，NLP）问题，采用一种新兴的优化算法——人工免疫算法（Artificial Immune Algorithm，AIA）求解NLP。该算法具有个体多样性好的特点，能有效避免早熟收敛。同时，对基本型AIA进行改进，在算法中加入引导因子以提高算法的局部寻优能力，得到引导型人工免疫算法（Guiding Artificial Immune Algorithm，GAIA），将其用于求解地球到火星的燃料最省小推力转移轨道。最后将GAIA寻优结果与间接法最优解进行对比，验证其最优性。

2 地球-火星小推力轨道转移问题

2.1 系统模型

地球到火星的小推力轨道转移过程可分3个阶段：地球逃逸段，星际巡航段和火星捕获段。在地球逃逸段和火星捕获段，最优推力方向可以用切向推力来近似，因此研究重点可放在星际巡航段的燃料消耗上。在星际巡航过程中，地球引力主导段主要位于巡航初期，约占整个过程的0.32%；火星引力主导段主要位于巡航末期，约占星际巡航过程的0.17%。故飞行器在星际巡航段大部分时间主要受太阳引力作用，可将地球和火星的引力摄动忽略。同时，地球轨道和火星轨道的偏心率均小于0.1，两轨道平面夹角小于2°，可将地球轨道和火星轨道简化为同平面的圆轨道。因此，可建立二维极坐标系（如图1所示）描述飞行器的运动，选择太阳为极点O，定义由太阳指向地球初始位置的射线为极轴Ox。飞行器的运动可由二维极坐标系下的位置速度摄动方程来描述，其形式如下：

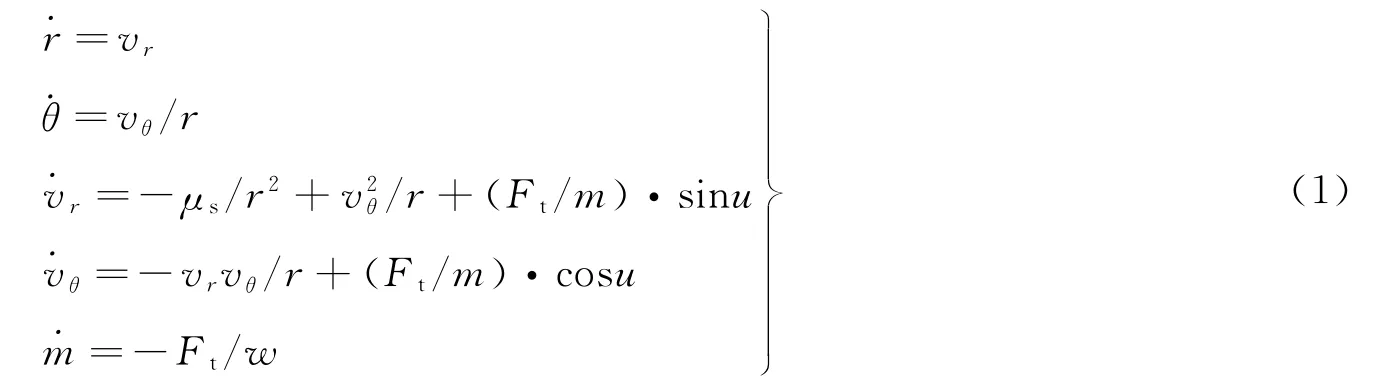
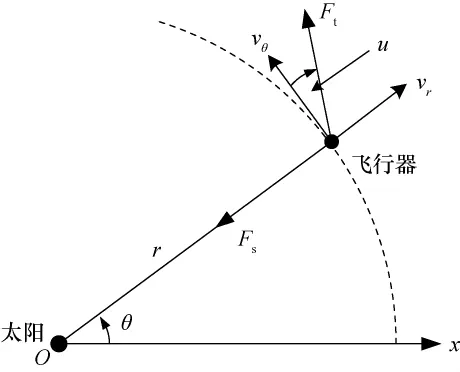
图1 地球-火星轨道转移极坐标系Fig.1 Polar coordinate system for Earth-Mars orbit transfer

式中r、θ、vr、vθ和m分别是飞行器的极半径 （日心距）、极角、径向速度、横向速度和质量；μs为太阳引力常数；Ft为发动机推力，其幅值假设为常数；u为推力方向角；w为排气速度。由于忽略地球和火星的引力，飞行器只受太阳引力Fs和小推力发动机推力Ft的作用。

巡航段中地球到火星的轨道转移可设为从地球轨道到火星轨道。初始条件为飞行器在地球轨道上运动，终端约束为飞行器到达火星轨道。令变轨初始时刻为t0＝0，终端时刻tf自由，相应的边界条件为

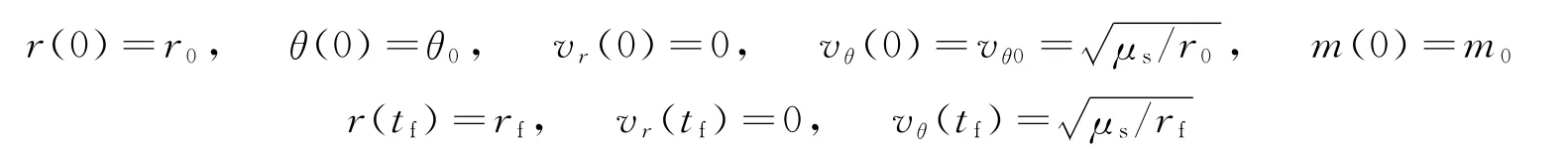
式中r0为地球轨道的日心距；θ0为飞行器在地球轨道上的逃逸点极角；m0为飞行器的初始质量；rf为火星轨道的日心距。

2.2 模型归一化

在小推力轨道优化过程中，由于各个状态变量的量级相差较大，寻优过程可能会丢失有效位数而难以收敛。为此，可将系统模型进行归一化处理。

1）首先定义两个参考变量r＊和m＊［2］，其表达式为r＊＝r0，m＊＝m0。

2）然后定义相关的归一化变量为

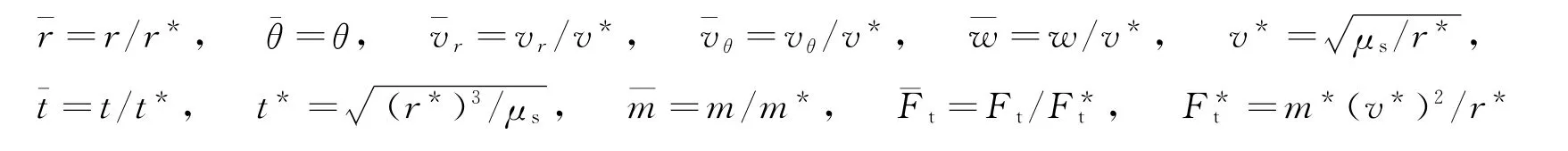
所有变量归一化后均为量纲为1的变量，且几乎处于同一数量级上。极角本身是量纲为1的变量，不进行归一化处理。

3）相应的状态方程变为

由式（2）可知，极角在状态方程中是解耦的，可先不考虑的状态变化。

4）相应的边界条件为

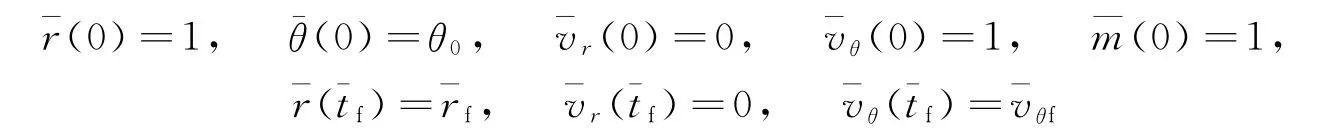
地球到火星的小推力转移轨道有很多条，为尽可能增加有效载荷的质量，需要设计一条燃料消耗最省的转移轨道，即要求以下性能指标达到最大：

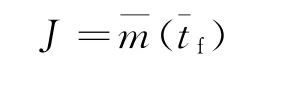
3 参数化及约束处理

3.1 控制函数参数化

在小推力轨道优化问题中，控制函数的搜索空间是一个泛函空间，不能直接应用优化方法进行求解，必须先将控制函数参数化。目前主要有3种参数化方法［7］：直接离散法、多段参数插值方法和函数逼近方法。这3种方法各有优缺点，本文采用一种新的方法——插值函数逼近法，其步骤如下：

1）采用函数逼近方法逼近控制变量函数。由维尔斯特拉斯 （Weierstrass）逼近定理可知，对在闭区间内连续的任何函数，都可用多项式级数一致逼近。本文的控制变量函数为闭区间内连续的函数，故可采用多项式函数进行逼近，其形式如下：

式中p＝1，2，…，N；N为幂函数的个数。

2）采用插值拟合的方法确定多项式函数的系数。

3）确定插值的特征点位置。采用直接离散方法，将最优控制问题的积分区间等分为M-1段，将M个时间节点上的控制向量设为特征点。

这种插值函数逼近方法的待优化变量少，具有明确的物理意义，容易猜测取值范围，同时计算速度快，函数逼近的精度高。

3.2 约束处理

小推力轨道优化问题是具有终端状态约束的最优控制问题，如何处理约束关系到直接法求解小推力轨道优化问题的成败。目前处理约束的方法主要有修复不可行解法和罚函数法。对于求解小推力轨道优化这类高维的非线性优化问题，罚函数法的应用效果更好。本文采用罚函数的形式定义评价函数faff（X）：

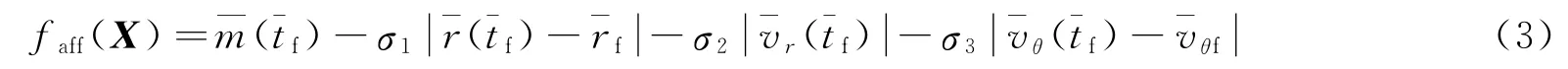
式中X为待优化量；σ1，σ2，σ3分别为3个惩罚项的权重系数。如果权重系数太小，起不到惩罚的作用，而权重系数太大又会影响全局寻优。因此，在寻优初期应放宽约束的惩罚，得到尽可能多的可行解以便寻找最优解；而在寻优后期应加大约束的惩罚，使不满足约束的可行解被淘汰，从而得到满足约束的最优解。为此，可吸取模拟退火算法的思想对权重系数进行自适应调整，其自适应调整规则如下：

式中λ＝1，2，3；β为温度下降系数，决定了权重系数的变化率，β∈［0，1］；Tλ为与σλ对应的初始温度，决定了权重系数最终值；g为当前迭代代数；gmax为最大迭代代数。为保证权重系数在寻优初期不会因数值太小而失去约束功能，将退火曲线值与常数1取最大值作为权重系数。

4 人工免疫算法

经过参数化和约束处理，小推力轨道优化问题转化为高维非线性规划问题。目前，非线性规划算法应用最多的是SQP。但SQP在求解优化问题时会出现病态梯度、初始点敏感和局部收敛问题。近年来，遗传算法（Genetic Algorithm，GA）由于不依赖梯度信息而在轨迹优化上得到广泛应用，但遗传算法容易陷入早熟收敛，局部搜索能力较差。本文采用AIA求解非线性规划问题，该算法具有寻优成功率高、个体多样性好的特点，不易陷入局部最优。

4.1 人工免疫算法原理

人工免疫算法模拟生物免疫系统，将待优化的问题对应抗原，可行解对应抗体，可行解的质量对应抗体与抗原的亲和度，将寻优过程与生物免疫系统识别抗原并实现抗体进化的过程对应起来，形成一种智能优化算法。

4.2 人工免疫算法设计

按照人工免疫算法原理，设计适合小推力轨道优化问题的人工免疫算法：

1）计算亲和度：由于AIA求解的是最优问题的最大值，因此可将亲和度取为式（3）所示的形式。这里，X为待优化抗体，在本文的小推力轨道优化问题中X＝［u1，u2，…，uM，］T。

2）计算浓度和激励度：在寻优过程中，AIA优化算法对浓度过高的抗体进行抑制以保持个体的多样性。抗体浓度fden（XI）计算方法为

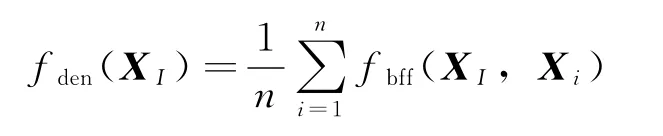
式中n为种群中抗体个数；XI为种群中的第I个抗体；fbff（XI，Xi）为抗体XI与抗体Xi的相似度，其表达式如下：

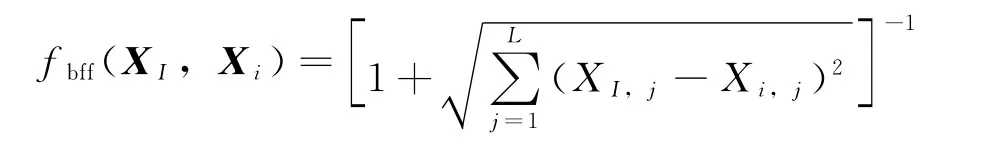
式中XI，j和Xi，j分别是抗体XI和抗体Xi的第j个变量；L为抗体个体的变量个数。

激励度计算方法［8］为

式中faff（XI）为抗体XI的评价函数，即亲和度；fden（XI）为抗体XI的浓度；a为计算参数，可根据实际情况确定。激励度是对抗体质量的最终评价结果，它综合考虑了抗体的亲和度和浓度。个体的亲和度越大，浓度越小，激励度越大。

3）免疫操作：首先根据激励度进行免疫选择，然后进行m次克隆、变异操作，实现局部搜索。变异操作采用如下规则：

式中XI，j，k是抗体XI的第k个克隆体的第j个变量；δ为定义的邻域范围；Pr是0和1之间的随机数；Pm为变异概率。最后进行克隆抑制，找出变异后的抗体及源抗体中亲和度最高的抗体AI替代源抗体XI，使得种群中抗体个数不变。

4）种群刷新：对激励度低的抗体，AIA将进行删除并随机生成新抗体Bi进行替代。

4.3 引导型局部搜索策略

基本型AIA的局部搜索机制可简单描述为克隆→变异→克隆抑制，盲目性较大，没有信息交换，导致AIA的局部搜索能力不强。本文将当前群体搜索到的最优解引入局部搜索中，得到了引导型人工免疫算法GAIA。相对基本型AIA，其变异算子改写为

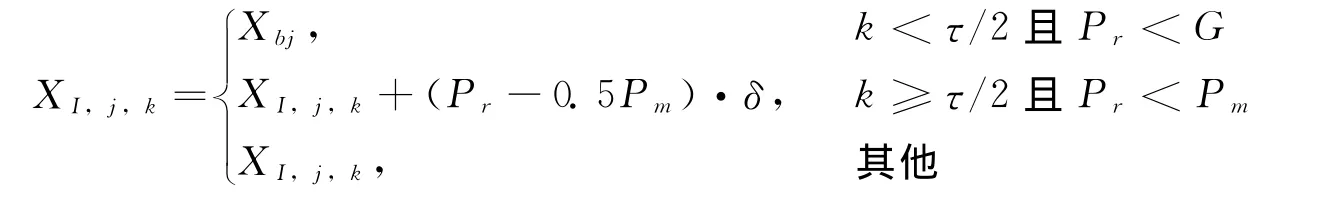
式中Xbj为当前种群的最优解Xb的第j个变量；τ为克隆数目；G为引导因子，取值为［0，1］，表示Xb对克隆体的引导强度。优化过程初期应取较小的引导因子，有利于全局搜索；优化过程末期应取较大的引导因子，有利于局部搜索。为此，定义引导因子的自适应调整公式如下：

式中b为调整参数；fb为当前种群最优抗体的亲和度；f0是引导因子G的跳变阈值。当fb接近f0时，引导因子G从较小值跳变到较大值，参数b可调整引导因子G跳变处曲线的变化趋势。优化前期f0取为1.01fb，优化后期f0取为0.99fb。若种群最优抗体的亲和度fb不再增大，则f0维持不变。

5 仿真及分析

地球轨道的日心距r0＝1AU（AU 为天文单位，1AU＝1.496×1011m）；太阳引力常数μs＝1.327 15×1020m3／s2；火星轨道的日心距为rf＝2.279 4×1011m；设飞行器在地球轨道的逃逸点极角为θ0＝-10°，初始质量为m0＝800kg，发动机推力为Ft＝0.5N，排气速度为w＝3.726 527×104m／s。在参数化方法中，取M＝10，N＝6。在罚函数法中，取β＝0.005，Tλ＝0.1 （λ＝1，2，3）。

由地球-火星小推力轨道转移的优化经验可知，推力角的前5个特征值在 ［0，π］内，后5个特征值在［π，2π］内。转移时间一般在200天以上，可设f取值范围为［3.5，4］。

人工免疫算法中，种群规模n＝100，最大迭代代数gmax＝100，克隆规模τ＝20，变异概率Pm＝0.8，激励度计算参数a＝2，引导因子G调整参数b＝150。由于GAIA是一种随机搜索算法，本文进行10次寻优仿真，并与自适应遗传算法 （Adaptive Genetic Algorithm，AGA）的寻优结果进行对比，如表1所示。将GAIA得到的最优归一化数据还原到真实模型，可得燃料最省的地球-火星小推力转移轨道，如图2和图3所示。

图2为GAIA求得的最优地球-火星小推力转移轨道的飞行轨迹。为验证GAIA寻优结果的最优性，将其与Pontryagin极大值原理 （间接法）求得的结果进行对比，如图3所示。由图3可知，采用这两种算法得到的小推力轨道转移结果基本相同。其中日心距和极角的变化曲线几乎重合，而径向速度和横向速度稍有差异但变化趋势相同，说明GAIA的优化精度高。GAIA求得的最优燃料消耗仅比间接法的结果多1.55%，其原因是多项式函数对最优控制函数的拟合存在一定误差 （如图4所示）。

图5为GAIA寻优过程中最大亲和度随迭代代数变化的曲线。由图5可知，GAIA在第10代就搜索到最优值附近，第40代完全搜寻到最优值。这说明GAIA的收敛速度比较快，同时局部寻优能力比较强，能够有效跳出局部最优点。

表1 GAIA和AGA的寻优结果Tab.1 Optimization results obtained by GAIA and AGA

图2 地球-火星小推力轨道转移最优轨迹Fig.2 Optimal Earth-Mars low-thrust trajectory

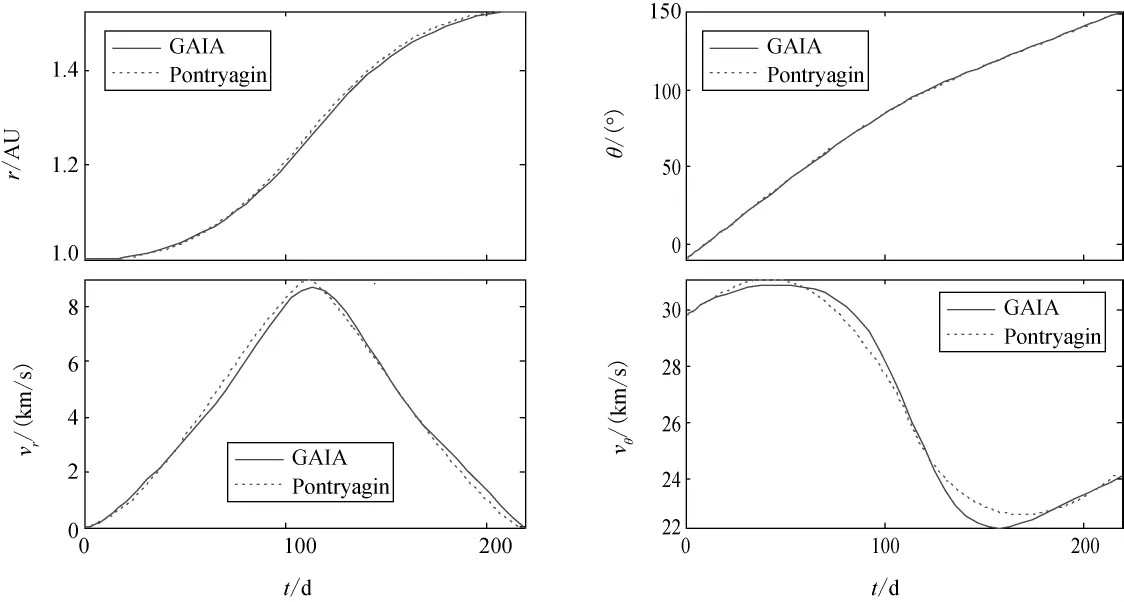
图3 状态变量变化曲线Fig.3 Time history of state variables

图4 推力方向角变化曲线Fig.4 Time history of direction angle of the thrust

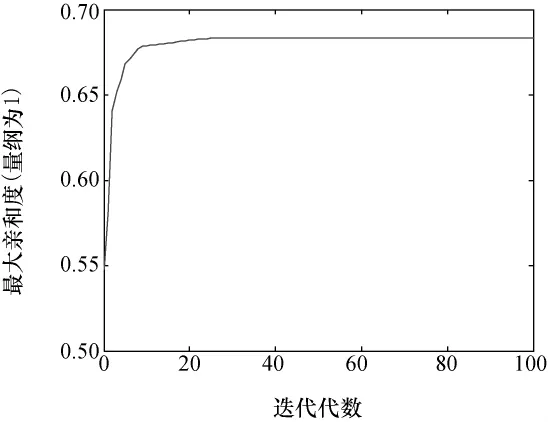
图5 最大亲和度随迭代代数变化的曲线Fig.5 Maximum affinity value of every generation

6 结束语

本文首先通过插值函数逼近法和自适应权重罚函数，将地火小推力转移轨道优化问题转化为NLP；然后在基本型AIA算法中加入引导因子以提高局部收敛能力，得到GAIA，并将其应用到地球-火星小推力转移轨道优化中。仿真结果证明，与AGA相比，GAIA能搜索到满足终端状态约束的最优地球-火星小推力转移轨道，局部寻优能力强；同时，该算法求得的最优轨道与间接法求得的结果近似，寻优精度高，且其求解难度比间接法小，不需要猜测初值，易于编程实现，鲁棒性好。通过仿真，证明了GAIA具有良好的全局和局部搜索能力，为其他优化问题提供了一种新的优化方法。

［1］REDDING D，BREAKWELL J V.Optimal Low-Thrust Transfers to Synchronous Orbit［J］.Journal of Guidance，Control，and Dynamics，1984，7（2）：148-155.

［2］CHUANG C H，GOODSON T D，HANSON J.Computation of Optimal Low-and Medium-Thrust Orbit Transfer［C］.AIAA Guidance，Navigation and Control Conference，Monterey，CA，Aug.9-11，1993：1391-1402.

［3］OBERLE H J，TAUBERT K.Existence and Multiple Solution of the Minimum-Fuel Orbit Transfer Problem ［J］.Journal of Optimization Theory and Applications，1997，95（2）：243-262.

［4］BETTS J T，ERB S O.Optimal Low Thrust Trajectories to the Moon ［J］.SIAM Journal of Applied Dynamical Systems，2003，2（2）：144-170.

［5］尚海滨，崔平远，栾恩杰.地球-火星的燃料最省小推力转移轨道的设计与优化 ［J］.宇航学报，2006，27（6）：1168-1173.SHANG HAIBIN，CUI PINGYUAN，LUAN ENJIE.Design and Optimization of Earth-Mars Optimal-Fuel Low-Thrust Trajectory ［J］.Journal of Astronautics，2006，27（6）：1168-1173.

［6］任远，崔平远，栾恩杰.基于退火遗传算法的小推力轨道优化问题研究 ［J］.宇航学报，2007，28（1）：162-166.REN YUAN，CUI PINGYUAN，LUAN ENJIE.Low-Thrust Trajectory Optimization Based on Annealing-Genetic Algorithm ［J］.Journal of Astronautics，2007，28（1）：162-166.

［7］陈刚，万自明，徐敏，等.飞行器轨迹优化应用遗传算法的参数化与约束处理方法研究 ［J］.系统仿真学报，2005，17（11）：2737-2740.CHEN GANG，WAN ZIMING，XU MIN，et al.Parameterization Method and Constraints TransformationMethod for RLV Reentry Trajectory Optimization Using Genetic Algorithm ［J］.Journal of System Simulation，2005，17（11）：2737-2740.

［8］孙宁.人工免疫优化算法及其应用研究 ［D］.哈尔滨：哈尔滨工业大学，2006.SUN NING.Artificial immune optimization algorithm and applications［D］.Harbin：Harbin Institute of Technology，2006.