交流伺服系统Ziegler-Nichols PI滑模并行复合控制*

张 营，吴文江，郭亚军

(1.济宁学院 物理与信息工程系，山东 曲阜 273155;2.中科院沈阳计算技术研究所，沈阳 110171;3.南京理工大学机械工程学院，南京 210094）

0 引言

永磁同步电机是机床传动的主要执行机构，但是由于控制模型中含有众多非线性因素，所以传统的PI控制方法对于机床这种变负载、多干扰系统只能整定出一组固定的PI参数，往往会出现超调量过大、过渡过程时间长，系统鲁棒性不强的缺点。

近年，虽然许多研究者将神经网络［1］、自适应控制［2-3］、模糊控制［4-6］、遗传算法［7-8］及专家系统等引入到PI参数整定中，克服了常规PI控制器的不足，但是由于智能及先进算法存在结构复杂、收敛速度慢和初值选定较难等［9］缺点，推广应用还存在较多问题。

国外学者 Rajani K.Mudi及 Chanchal Dey等人［10］根据误差的变化趋势，通过设定调节因子，对经典控制器的比例积分参数进行实时调节，从而达到改善系统控制特性的目的。因此本文根据伺服系统静动态指标，将这种控制策略应用到交流伺服系统的位置控制中，通过仿真实验，验证了该控制器实施的可行性。

1 并行复合控制器设计

并行复合控制主要是根据切换控制理论，通过设定误差值，使两种算法在系统中进行切换使系统达到最佳状态，由此分别设计滑模控制器和Ziegler-Nichols PI控制器，在此基础上得到并行复合控制结构。

1.1 位置环滑模控制器设计

由于速度环响应远比位置响应快，即位置环截止频率远小于速度环各时间常数的倒数。

在推导控制率时，可将速度环等效为一阶惯性环节。

令e2=，考虑位置给定为阶跃信号情况下可得状态方程为:

取位置滑模线性切换函数为:

式中，c3为正常数。

令位置环滑模变结构控制器输出为:

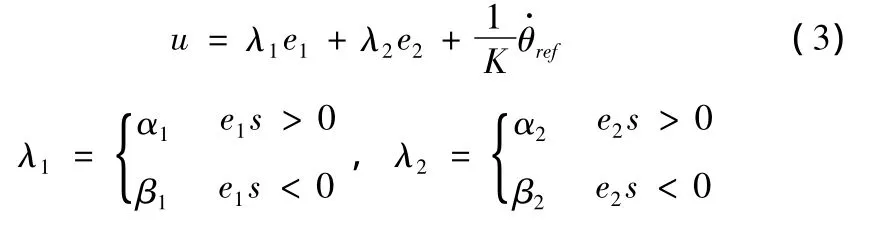
由滑模到达条件可得位置环滑模变结构控制器参数为:

1.2 Ziegler-Nichols PI控制器设计

Ziegler-Nichols PI控制器的基本组成为调节因子、误差函数、误差变化率函数及调节速率等，控制器结构原理如图1所示。图1中α为调节因子，ΔeN为归一化后的误差变化率，eN归一化后的误差，k为反馈系数。其中ΔeN及eN可分别表示为:

式中，ωref为给定值，ωf为反馈值，ωref-max为给定值的最大值，e(k）为误差。

图1 控制器结构框图

由式(5）～(7）可推出调节因子α为:

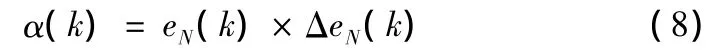
经典数字PI控制算式通常为:

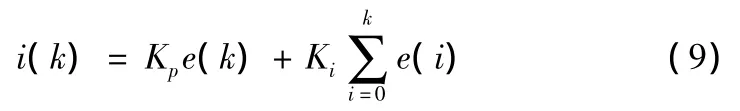
式中，i(k）为控制输出，Kp为比例系数，Ki为积分系数。

将(8）式代入以下调节函数可得:

式中，k1为比例调节速率，k2为积分调节速率为修正后的比例系数为修正后的积分系数。

根据式(8）与式(10）可得到调节因子α在闭环系统中始终处在范围-1～1之间，由以上分析得出Ziegler-Nichols PI控制算式为:

式中，i*为控制器输出。

由以上的分析可推出复合控制简化原理图如图2所示。

2 基于电流解耦控制的永磁同步电动机线性化数学模型

假设:①不考虑饱和效应;②电动机的气隙磁场为均匀分布，且感应反电动势为正弦波状;③不计磁滞与涡流损耗;④励磁电流没有动态响应;⑤转子无励磁绕组;⑥采用转子磁极位置定向矢量控制定子电流励磁分量Id=0。

根据如上假设，可写出转子坐标系即dq坐标系下系统的线性化数学模型。

式中，ud，uq为dq坐标系上的电枢电压分量;iq，id为dq坐标系上的电枢电流分量;L为dq坐标系上的等效电枢电感(L=Ld=Lq）;R，ωr为电枢绕组电阻和dq坐标系的电角速度;Ψf，pn为永久磁铁对应的转子磁链和电机极对数。

3 仿真及实验

根据数学模型分别设计滑模控制器和Ziegler-Nichols PI复合控制器。主要参数如下:电机及负载转动惯量经折算后为J=2.627×10-3kg·m2;摩擦力矩经折算后为4.86N·m;系统外部干扰力矩及未建模动态折算后为10N·m，电磁转矩系数Kt=1.11N·m/A;阻尼系数B=1.43×10-4N·m·s;定子电阻Ra=2.6Ω;绕组电感Ld=Lq=50×10-3H;额定电流Ie=6.4A;容许最大电流Imax=12.8A;磁极对数Pn=4。滑模控制器参数取:c3=47，α1=11，β1=-14，α2=0.02，β2=-0.005。Ziegler-Nichols PI控制器仿真参数取:Kp=10，Ki=1.2，k1=1.5，k2=2.4，α=0.5。复合控制器误差设定值为0.08。PI控制器位置环参数取kp1=10，kI1=0.01。

图2 并行复合控制结构

(1）常值负载干扰

假设仿真在第1s时加入一个阶跃扰动10N·m，系统在PI控制和滑模Ziegler-Nichols PI复合控制下位置输出响应曲线如图3及图4所示。从图中可以看出，采用传统PI算法具有较快的上升时间，当负载出现扰动时，位置响应出现较大的偏移，并且需要较长时间才能恢复到平稳位置。而采用滑模Ziegler-Nichols PI复合控制时，系统具有较强的抗干扰能力，受外界作用力较小，并且短时间内能达到平衡状态。

图3 施加负载扰动时的传统控制响应曲线

图4 施加负载扰动时的复合控制响应曲线

(2）系统参数摄动

为了验证伺服系统参数发生摄动时的控制效果，假设系统转动惯量由J=2.627×10-3kg·m2变为J=5.254×10-3kg·m2，分别对系统采用以上两种控制方案，得到位置响应曲线如图5及图6所示。从图中可以看出，采用PI控制时，系统出现了较大超调，之后又趋于平稳。而采用滑模Ziegler-Nichols PI复合控制时，系统响应超调较小，调节时间短。

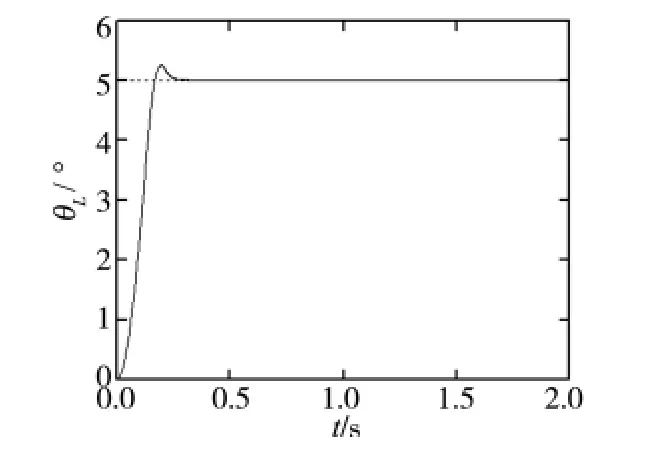
图5 转动惯量变化时的经典控制响应曲线

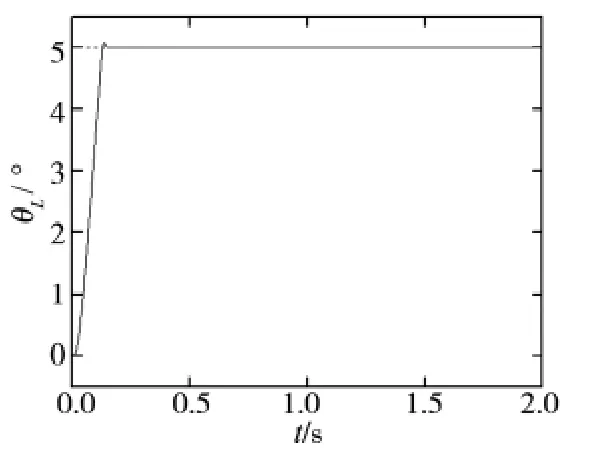
图6 转动惯量变化时的复合控制响应曲线

(3）正弦跟踪实验

系统的跟踪目标函数为:65sin(0.7166t），其跟踪误差曲线如图7和图8所示。从图中可以看出，复合控制相对于传统PI控制有好的跟踪特性，误差较小。

图7 传统控制误差曲线

图8 复合控制误差曲线

4 结束语

本文针对交流伺服系统的位置控制，结合滑模变结构控制理论和Ziegler-Nichols PI控制理论的优点，提出了一种并行复合控制策略。通过对系统位置环的分析，建立了滑模变结构位置环控制器和Ziegler-Nichols PI控制器。仿真结果表明，当系统的参数摄动及受外部扰动时，该控制方案能实现系统的鲁棒控制。滑模控制在较强鲁棒性的前提下，保证了系统跟踪的位置误差。Ziegler-Nichols PI控制实时调节系统控制器参数，减少了控制效果对人为因素的依赖。同时可以看出，算法的推导较为简单，曲线响应满足系统要求，初值选定只需要简单调节既能使动态响应符合要求。

［1］赵希梅，郭庆鼎.PMSM伺服系统的转动惯量辨识和控制器参数优化［J］.组合机床与自动化加工技术，2009(11）:75-77.

［2］Yu Jinpeng，Chen Bing，Yu Haisheng.Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping［J］.Nonlinear A-nalysis:Real World Applications，2011，12(1）:671-681.

［3］Jun Lu，Hai Xin Zou，Lie Shen，et al.Application of Adaptive Fuzzy-PID Control in Servo Spindle Rigid Tapping［J］.Advanced materials Research，2011，301-303:1477-1481.

［4］Kong Xiaohong，Zhang Baojian，Mao Xinhua.Design and Application of Self-Tuning PI Controller［J］.Applied Mechanics and Materials，2010，43:160-164.

［5］叶汉民，朱伟.基于滑模变结构及模糊控制的异步电机调速系统的研究［J］.组合机床与自动化加工技术，2011(6）:74-77.

［6］孙夏娜，俞群明，周兵，等.主动悬架单神经元模糊PID控制策略与仿真［J］.系统仿真学报，2009，21(8）:2165-2168.

［7］Jan Rong-Maw，Tseng Chung-Shi，Liu Ren-Jun.Robust PID control design for permanent magnet synchronous motor:A genetic approach ［J］.Electric power systems research，2008，78:1161-1168.

［8］郝齐，关立文，王立平.基于遗传算法并联机床电机伺服系统控制参数整定［J］.清华大学学报，2011，50(11）:1801-1806.

［9］彭继慎，王强，刘栋良，等.永磁同步电动机的速度自适应反推控制［J］. 煤炭学报，2006，31(4）:540-544.

［10］Rajani K.Mudi，Chanchal Dey，Tsu-Tian Lee.An improved auto-tuning scheme for PID controllers［J］.ISATransactions，2009，48:396-409.