金属平片冷表面湿空气凝水过程热质传递特性的数值模型
2012-11-23胡海涛庄大伟韩维哲熊伟丁国良
胡海涛, 庄大伟,韩维哲,熊伟,丁国良
(上海交通大学 制冷与低温工程研究所,上海 200240)
0 引言
翅片管换热器应用范围广泛,换热器翅片侧在蒸发工况下普遍存在凝水现象,从而对翅片冷表面的热质传递特性产生影响[1]。研究空气凝水过程中的热质传递特性,对于翅片结构的优化设计和提高换热器空气侧传热性能有重要意义[1]。文献中已有大量关于析湿工况下翅片侧空气的流动和换热特性研究,但是目前大多数研究都是基于实验方法,如Wang等人[2,3]的研究着重于实验研究各种翅片形式在湿工况下的传热特性分析,而湿工况下空气侧热质传递方面的数值仿真研究则很少,尤其对于翅片管换热器的研究缺乏相关的研究报道。
Comini等人[4-6]进行了湿工况翅片表面热质传递的数值研究。他们在研究中假设一旦水蒸气凝结,其生成的液态水将立刻从固体表面去除[6],即忽略了固体表面已经冷凝下来的水滴或水膜的影响。其他研究人员,如Yang等人[7],采用CFD方法对湿工况下翅片管换热器进行了模拟,同样忽略了冷凝水滴或水膜带来的影响。目前已有的数值模型模型假设冷凝过程仅发生在空气和翅片的分界面上,仅考虑了气相和液相之间的传质。但是,实际析湿凝水过程中,除了相间传质外,当水蒸气分压力达到饱和时,如果空气温度进一步降低则水蒸气可直接析出,此时冷凝过程属于核态冷凝。
因此,为了从机理上更准确地对翅片管式换热器中的热质传递过程进行描述,有必要建立一个新的热质传递数值模型,能够同时对以上两种传质现象进行模拟。
1 湿空气凝水过程热质传递特性的数值模型
1.1 湿空气凝水过程分析及模型假设
如图1(a)显示了翅片管换热器的示意图,所研究的翅片形式为平片且翅片间距相等,换热管呈交错排列。在实际工况中,翅片不仅和换热管之间存在热传导,并且和来流空气之间也存在对流换热,因此对于换热的计算涉及到热传导和对流换热共轭问题的求解;另外,由于析湿现象的存在,湿空气中的水蒸气凝结后也会带来相变所引起的能量传递。因此,能量方程的求解不仅需要包括流体区域而且需要涵盖部分固体区域(翅片及换热管壁),如图1(b)中的灰色区域所示。

图1 翅片管换热器示意图
模型假设:湿空气仅由干空气和一定质量的水蒸气组成,当水蒸气发生凝结后,液态水会立刻从翅片表面流走[6]。因此,本文中的计算不考虑液态水滴或水膜在翅片表面的滞留以及由此而带来的对温度场和空气流场的影响。
当翅片表面温度低于来流空气的露点温度 Tdew时,水蒸气开始凝结。假设在翅片表面已有冷凝水,则水蒸气冷凝过程,包括气液相间传质、直接冷凝两种传质方式,如图2所示。

图2 翅片表面传质过程示意图
凝水过程中,气液相间传质与直接冷凝两种传质过程的分析如下所述。
1)相间传质:指的是空气中的水蒸气和已冷凝的液态水之间的质量传递,仅发生在相分界面上。假设其驱动力是由相间的浓度差所引起的,水分子的不规则运动造成了质量从高浓度往低浓度的净转移,传质的方向则决定于各相之间的浓度差。
2)直接冷凝:当某控制容积的温度低于 Tdew时且所含水蒸气分压力已达到饱和,空气中的水蒸气可直接析出为液态水滴或水雾,这样的质量传递并不一定需要发生在气液分界面上,可采用经典成核理论进行求解。成核现象通常发生在气体或液体接触面的成核点上,悬浮颗粒或气泡同样也能成为成核点,这样的成核为非均匀成核;而均匀成核则不需要成核点,它是一种自发和无规则的现象,需要一定的过热度或过冷度[8]。
1.2 数学模型的建立
由于能量方程的求解中仍然会考虑到相变带来的潜热传递,潜热的产生会影响到翅片表面的温度分布,而翅片温度又会影响到界面上的水蒸气的质量分数,因此对于湿工况下空气侧的计算,实际上就是对于在边界层中的温度场和水蒸气的浓度场耦合方程的求解。
如图1(b)中虚线所示的部分为数值模拟的控制单元,该控制单元的数学模型除了包括质量、动量和能量守恒方程外,还应包括组分守恒方程。
质量、动量方程、能量方程分别为:

其中,∆M为析湿总量,hfg为水的比潜热;两者的乘积反映了由于水的冷凝而造成的潜热传递,作为源项添加在能量方程中,用以反映析湿过程中的潜热传递。
由于是一个多组分多相问题的求解,控制方程中还需要添加一个组分守恒方程,如下所示:
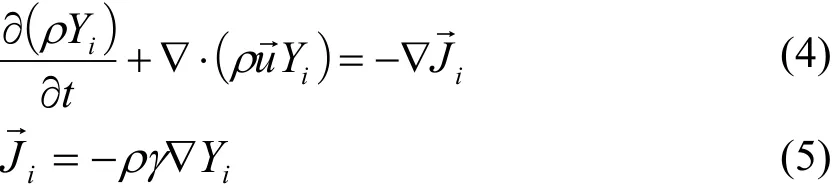
式中,Yi为第i种组分的质量分数;Ji为第i种组分的扩散通量,γ为质量扩散系数。
模型开发的关键,是得出数学模型中的析湿总量 ∆M。按照前面分析得出的析湿过程,析湿总量∆M 为气液相间传质的析湿量、直接冷凝析湿量之和。
下面分别介绍气液相间传质析湿量与直接冷凝析湿量的数学模型。
1.3 相间传质模型的开发
图3(a)显示了翅片管换热器示意图,假设在翅片表面上有冷凝水存在,如图3(b)所示,冷凝水上则被湿空气所包围。定义湿空气为主相,与之接触的冷凝水为邻相。如果假设T-T表面为在邻相中靠近相分界面的一个有限距离的表面,则在T-T表面上不存在有浓度或温度的梯度场;另外假设0-0表面是主相中离相分界面无限近距离的一个表面,即在边界层中,那么0-0表面上的水蒸气达到饱和状态,其含湿量为饱和含湿量Ws。∞-∞表面为主流湿空气。

图3 相间传质过程示意图
基于以上假设,如果考虑这样一个控制容积,这个控制容积包含了相分界面,上下表面分别为0-0表面和T-T表面,那么对于某单独组分可以列出相应的守恒方程如下:

移项可以得到传质速率m˙":

其中,mj为 j组分的摩尔浓度或质量浓度;γj为 j组分的质量扩散系数;下标0和T分别代表0-0和T-T表面的值;n为相分界面的法向矢量。
对于本文中的气态水和液态水之间的传质,公式(7)可以写成:

0-0表面和T-T表面上的边界条件如下:

将公式(9)带入式(8)中可以得到相间的传质速率为:

上式中,D为二元混合物的扩散率;w为含湿量;s代表饱和状态。
1.4 直接冷凝模型的开发
根据经典成核理论,水蒸气的成核速率I决定于临界团聚体的数目 n*和分子与团聚体之间的扩散率β,其计算公式为:

式中,N为单位容积内潜在的成核点;kB为波尔兹曼常数(1.38065×1023J/K)。∆G*为临界自由能改变量,对于均匀成核来说,其计算公式为:

而非均匀成核的冷凝过程更易发生,非均匀成核的临界自由能改变量计算如下[9]:

其中,下标heter和hom分别表示非均匀成核和均匀成核;f(m,x)为水滴接触角θ和外来粒子的半径Rs的函数,计算方法如下:

1.5 数学模型的求解
为了能够正确地计算析湿过程中的凝水量,通过UDF将1.3节和1.4节中开发的传质模型加入1.2节的控制方程中,并采用CFD软件(FLUENT)对控制方程同时进行求解,可以获得空气侧的传热系数hc和传质系数hm;与之对应的无量纲参数j因子分别为:

式中,Gmax为流过翅片间最窄处的空气质量流速,kg/m2·s;Cp,a为空气侧比容,J/kg·K;Sc为施密特数。
2 数学模型的实验验证
为了验证空气侧热值传递数值模型的准确性,本文对数值模型的计算结果与文献中实验数据[10-13]进行对比了对比。
图4给出不同空气入口相对湿度情况下,数值仿真结果和实验数据之间的对比。
由图4可以看出,jh和jm的数值解随雷诺数的增大而不断下降,其变化趋势和实验数据完全一致。对于空气侧对流换热来说,jh的数值仿真结果和实验数据吻合的较好,两者的平均相对误差为6.93%,数值模型对于 96%的实验数据预测误差在±15%以内。
从图4(a)和(c)中可以看出,对于两种不同入口相对湿度,数值解普遍过高地预测了空气侧对流换热系数,这是由于本文模型假设换热器排水性能良好,翅片表面没有粘附液态水滴,而在实验中,翅片表面往往存在液态水滴或水膜造成了空气侧和翅片表面之间的热阻,从而降低了对流换热量。另一方面,对于空气侧传质来说,jm的计算结果和实验数据之间的误差随着雷诺数的增加而降低,两者的平均相对误差为12.1%,数值模型对于91%的实验数据点的预测误差在±20%以内。当空气侧入口相对湿度RH = 50%且雷诺数Re > 4000时,实验传质系数突然增加,而数值模型并没有这个现象,这是由于当主流空气的流速增大时,原来粘滞在翅片上的冷凝水被空气吹离或者随着主流空气被夹带出换热器,因而在翅片表面留下更多的空间使得更多的水蒸气得以冷凝,因而造成了传质系数的增加[11];而本文模型不考虑冷凝水被空气吹走或夹带,故计算得出的传质系数会小于实验数值。
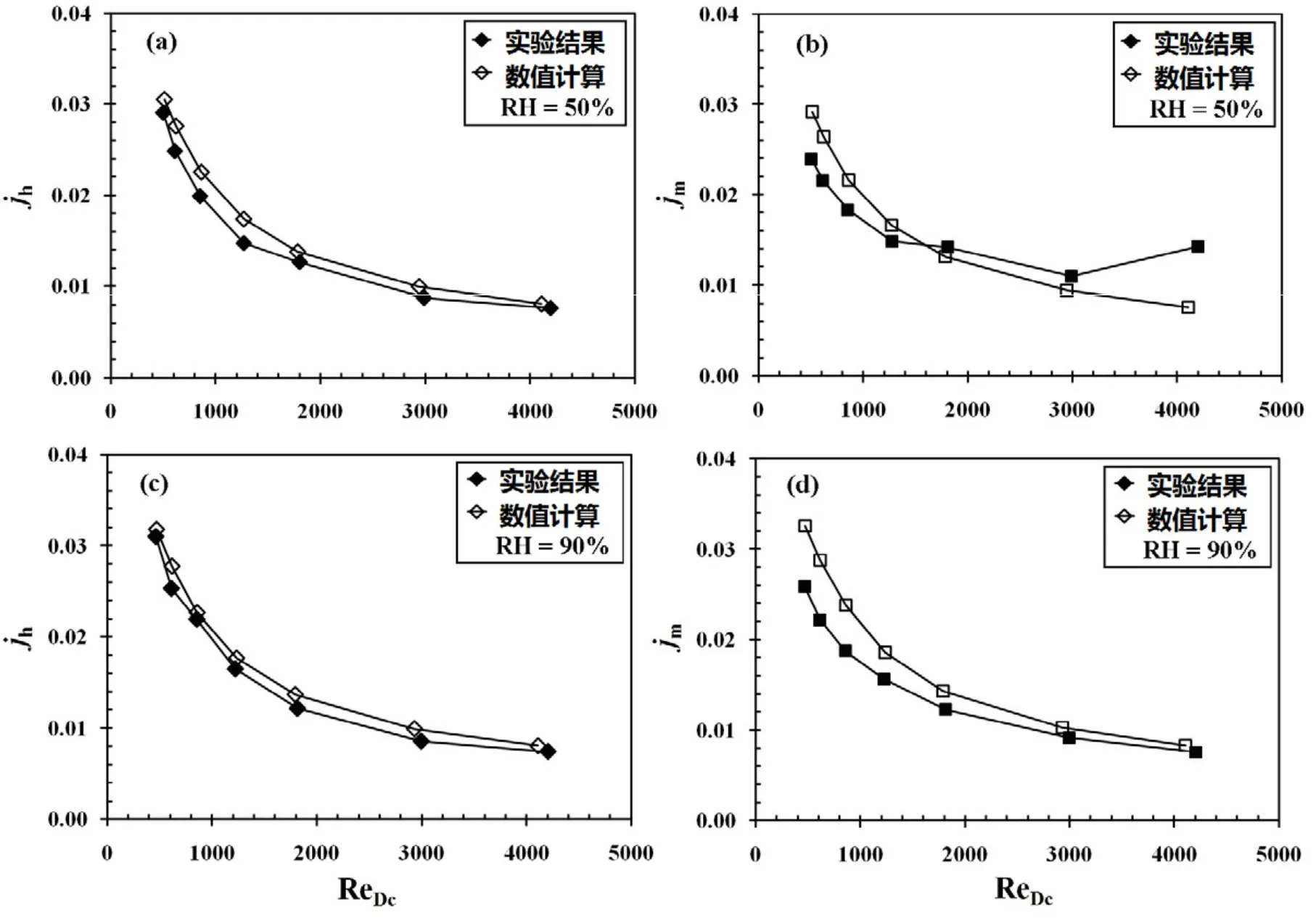
图4 jh和jm的数值仿真结果和实验数据之间的对比
3 结论
(1) 建立了湿工况下翅片管换热器空气侧热质传递的数值模型,模型包括了气液相间传质过程和水蒸气的直接冷凝模型,从而使模型能够反映析湿过程的机理。
(2) 通过对模型的验证表明,新模型的精度较好,对于传热来说,96%的模型预测结果和实验数据的误差在±15%以内,平均相对误差为6.93%;对于传质来说,91%的模型预测结果和实验数据的误差在±20%以内,平均相对误差为12.1%。
[1] R M Manglik, J Zhang, A Muley. Low Reynolds number forced convection in three dimensional wavy-plate-fin compact channels: fin density effects [J]. International Journal of Heat and Mass Transfer, 2005, 48: 1439-1449.
[2] C C Wang, Y T Lin, C J Lee. An airside correlation for plain fin-and-tube heat exchangers in wet conditions [J].International Journal of Heat and Mass Transfer, 2000, 43:1869-1872.
[3] C C Wang, W S Lee, W J Sheu, et al. A comparison of the airside performance of the fin-and-tube heat exchangers in wet conditions: with and without hydrophilic coating[J]. Applied Thermal Engineering, 2002, 22: 267-278.
[4] G Comini, G Croce. Convective heat transfer and mass transfer in tube-fin-exchangers under dehumidifying conditions [J]. Numerical Heat Transfer, Part A, 2001, 40:579-599.
[5] G Comini, C Nonino, S Savino. Convective heat and mass transfer in wavy finned-tube exchangers [J].International Journal of Numerical Methods for heat &fluid flow, 2002, 12(6): 735-755.
[6] G Comini, C Nonino, S Savino. Numerical evaluation of fin performance under dehumidifying conditions [J].Journal of heat transfer, 2007, 129: 1395-1402.
[7] B Yang, S C Sekhar. Numerical algorithm study of CFD modeling for a compartmented cooling coil under dehumidifying conditions [J]. Numerical Heat Transfer,Part A, 2007, 52: 737-755.
[8] Y Viisanen, R Strey, H Reiss. Homogeneous nucleation rates for water [J]. Journal of Chemical Physics, 1993,99(6): 4680-4692.
[9] M Yang, H L Dai. Heterogeneous nucleation and wetting of water thin films on a metal surface: A study by optical second harmonic generation [J]. Journal of Chemical Physics, 2003, 118(11): 5106-5114.
[10] W Pirpmpugd, S Wongwises, C C Wang. A tube-by-tube reduction method for simultaneous heat and mass transfer characteristics for plain fin-and-tube heat exchangers in dehumidifying conditions [J]. Heat Mass Transfer, 2005,41: 756-765.
[11] W Pirpmpugd, C C Wang, S Wongwises. Finite circular fin method for heat and mass transfer characteristics for plain fin-and-tube heat exchangers under fully and partially wet surface conditions [J]. International Journal of Heat and Mass Transfer, 2007, 50: 552-565.
[12] W Pirpmpugd, C C Wang, S Wongwises. A fully wet and fully dry tiny circular fin method for heat and mass transfer characteristics for plain fin-and-tube heat exchangers under dehumidifying conditions [J]. Journal of Heat Transfer, 2007, 129: 1256-1267.
[13] W Pirpmpugd, C C Wang, S Wongwises. Heat and mass transfer characteristics for finned tube heat exchangers with humidification [J]. Journal of Thermophysics and Heat Transfer, 2007, 21(2): 361-371.
