基于菱形阵列的弹丸落点定位模型研究

刘新爱，狄长安，孔德仁

(南京理工大学 机械工程学院,江苏 南京 210094)

在靶场试验中，精确定位弹丸的落点是测试并判定弹丸性能和威力的必要前提，根据弹丸落点提供的参考信息，可以对炮弹的运行轨道进行分析及回收炮弹引信等装置进行检测。目前，定位技术主要分为有源定位和无源定位两类，其中无源定位是通过获取目标自身的光、热、声、电等信号实现定位，具有定位精度高、安全性好等优点。弹丸落地产生的振动信号分别在空气和地质层中进行传播，即形成声波和地震波。以往检测弹丸落点大多利用爆炸声波进行定位，声波传输时易受介质温度、风速、灰尘等影响，特别是当炮弹落地未发生爆炸时，声波信号很微弱，声学法定位的精度明显降低。而地震波信号直接体现了弹丸落地时的冲击特性，可利用弹丸落地的地震波信号实现落点的定位，地震动探测具有探测距离远、抗电磁能力强、隐蔽性好等优点。

由于靶场场地范围大，单一传感器的定位误差较大，可以采用多传感器融合技术[1]，在某些特殊情况下，弹丸落点的区域可能比较大。因此，笔者提出了一种传感器布阵方法，在3 km×3 km的靶场范围内，具有较好的适用性，为弹丸的落点检测提供了有力的参考。

1 定位基本原理

弹丸落地时对地面产生强烈的冲击，引起地质层发生变形，该变形以地震波的形式传播出去[2]。地震波的传播波形主要有P波(纵向压缩波)、N波(纵向稀疏波)、S波(横波)和R波(瑞雷波)，其中P波传播最快，频率较高，R波传播最慢。瑞雷波大约占地震波总能量的2/3,因此，一般选取R波作为检测地震波的有效信号[3-4]。

阵列模型中的传感器阵元检测到地震波信号(如图1)，通过分析采集的地震波信号，选取地震波波形中第1个峰值作为特征点，得到信号到达各个传感器之间的时间差，再结合传感器的布阵模型和数学算法得到弹丸的落点坐标(x,y)。

2 传感器布阵和数学模型

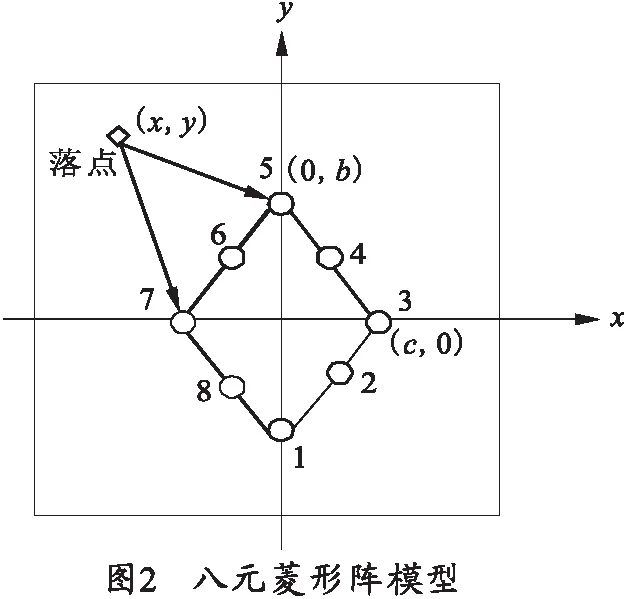
传感器的布阵方法是采用菱形阵列，该阵列模型可对整个靶场区域的地震波信号进行检测，并且可以结合菱形的几何特征，调整菱形对角线的取值，以达到提高数学模型定位精度的目的。以靶场的中心为坐标原点，建立如图2所示的数学模型，图中共8个传感器，等间距地分布在菱形的四条边上，分别编号为1,2,…,8，其中b和c是模型参数，分别对应菱形长、短对角线的一半。设弹丸落点坐标为(x,y)，传感器坐标为(xi,yi)(i=1,2,…,8)。假设地震波在地表介质中匀速直线运动且每个传感阵元均能检测到地震波信号，由于各个传感器在Oxy坐标平面内位置不同，所以当地震波以速度v0传播到各个传感器时所需的时间不同，利用地震波信号传播的时间差Δt和s=v0×t联立，可得到相邻两传感器满足如下的数学关系式：

(ti-ti-1)·v0(i=1,2,…,8)

(1)

式中:ti表示地震波到达第i个传感器所用的时间，根据数学模型可以建立28个方程，在上式中有x，y，v03个变量，理论上方程组中有3个方程即可求得解，但是为了提高解的精度，需多个方程联立，利用最小二乘迭代的方法求坐标点(x,y)。

3 数学模型仿真分析

用MATLAB对定位模型进行仿真和误差分析，判断菱形布阵的适用性。考虑到靶场布阵时的易操作性、安全性和模型稳定性，在距靶场中心25 m×25 m范围内集中布阵。为了保证在3 km×3 km的靶场范围内定位的准确性，满足误差不超过5 m的定位要求，将靶场分为几个区域[5](如图3所示)，分别对各区域边界进行仿真分析。

图3中由下至上沿-1 500,-1 100,-700,-300,-100,100,300,700,1 100,1 500 m进行区域划分。因为菱形关于x轴对称，所以只需讨论x轴正半轴5个区域的定位精度，如果定位模型的仿真误差在允许范围内，那么对于整个靶场该定位模型同样适用。

参数b、c的取值直接决定菱形布阵模型的定位精度，在25 m×25 m布阵范围内，为了方便讨论，设定参数c=12 m，b取不同的值，分析5个区域边界的定位误差，讨论b值对定位精度的影响。通过分析可以确定b、c的一组最佳值，得到理想的菱形布阵模型[6-7]。仿真过程如下：(仿真图中x轴表示每个仿真区域的点序列，y轴表示定位误差)

1)b=8 m时，仿真结果如图4所示。

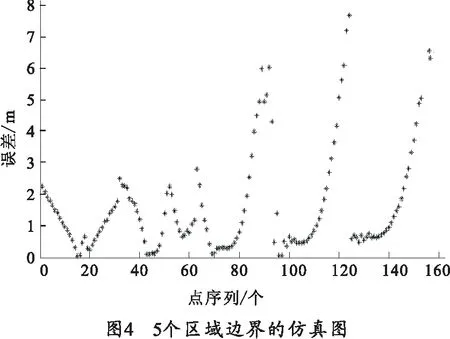
由上述仿真图分析可得：b=8 m时，模型的定位精度比较差，虽然靠近靶心300 m的区域内，其测量误差小于3 m，但是随着检测范围的增大，定位误差也逐渐增大，特别是靶场边界附近，某些区域的定位误差已经超过7 m，不能满足定位精度的要求。增大b的值，观察定位精度的变化。

2)b=12 m时，仿真结果如图5所示。

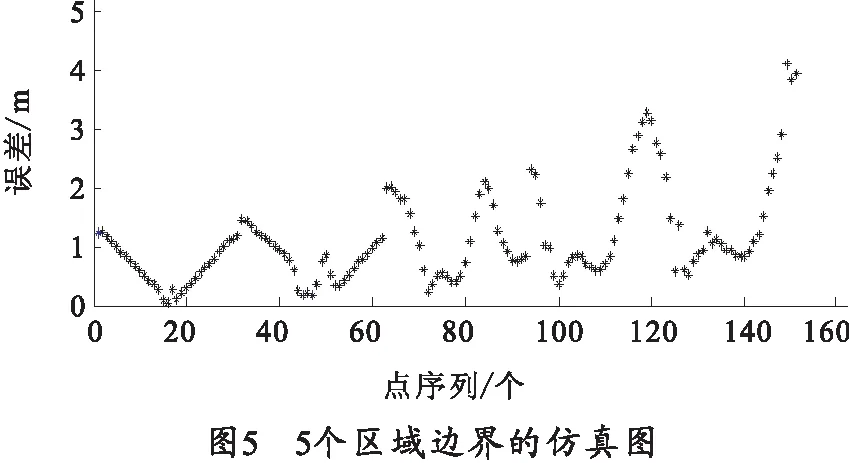
由图5可得，随着b值的增大，5个区域边界的定位误差明显减小，定位精度有了很大提高。靠近靶心的区域，定位误差已经在1.5 m以下，远离靶心的边界区域误差均已在5 m以下，有效测量范围增大，已经基本满足定位要求。于是，推测b值增大，定位精度提高。下面再增大b，观察误差的变化情况。

3)b=14 m时，仿真结果如图6所示。

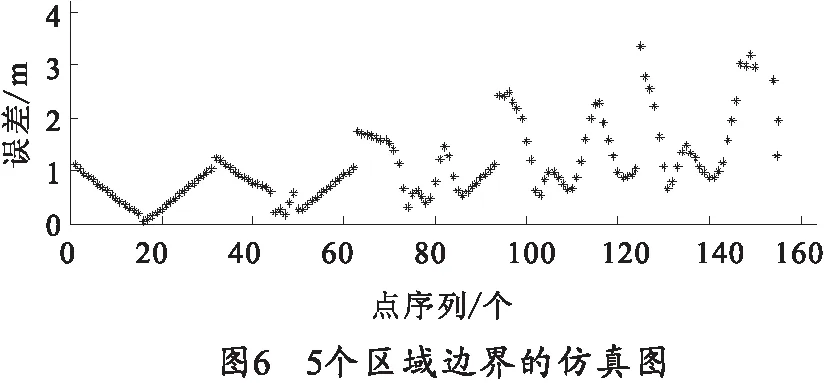
4)b=18 m时，仿真结果如图7所示。

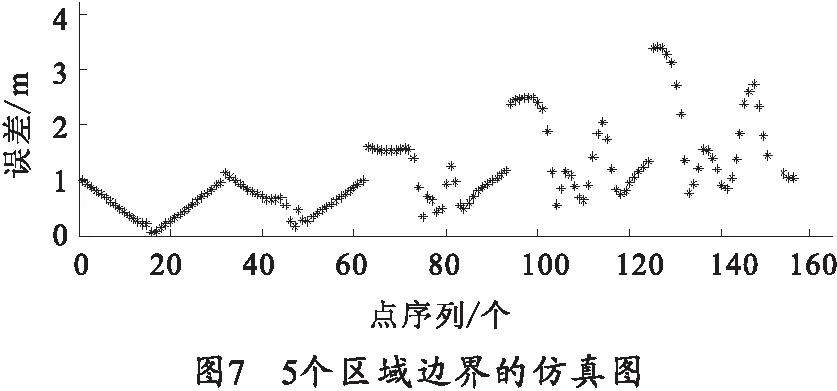
综合3)、4)两种情况的仿真图可得，模型的定位精度较情况2)有所提高，5个区域边界的定位误差都在3 m以下，特别是情况3)的仿真结果，定位精度更理想。可见，b值增大，定位精度提高。此外，相比图6的仿真结果，图7表明，靠近靶心的区域，定位精度均能满足要求，但是在远离靶心的区域，定位精度有所下降。由此可得，b值不能无限增大。

5)b=22 m时，仿真结果如图8所示。

情况5)的仿真结果表明，b值再继续增大时，远离靶心区域的定位精度不仅降低，而且在靶场有效测量范围内，系统稳定性降低。由此可得，在允许布阵范围内，b/c的比值要满足一定的关系，才能保证在有效测量范围内模型的定位误差最小。

4 结 论

经过对b不同取值的定位误差分析可得，合理地选取参数b、c的值，菱形布阵模型能够满足定位精度的要求，误差达到3 m以内。各个仿真结果表明，在c值固定的情况下，当1

[1] 彭冬亮，文成林，薛安克.多传感器多源信息融合理论及应用[M].北京:科学出版社，2010:5-30.

PENG Dong-liang,WEN Cheng-lin,XUE An-ke.Multi-sensor and multi-source information fusion theory and application[M].Beijing:Science Press，2010:5-30.(in Chinese)

[2] 胡广新，赵向阳.基于弹头落地的地震波测量落点坐标[J].装备指挥技术学院学报，2006，17(2)：116-120.

HU Guang-xin，ZHAO Xiang-yang.Measuring the target coordinates according to the target geodetic coordinates with seismic[J].Journal of the Academy of Equipment Command & Technology，2006，17(2)：116-120. (in Chinese)

[3] 蒋萍，狄长安，孔德仁，等.基于声学立靶的传感器阵列模型研究[J].火炮发射与控制学报，2011(4)：38-40.

JIANG Ping, DI Chang-an, KONG De-ren, et al.Research for sensors array model based on the acoustic target[J]. Journal of Gun Launch & Control，2011(4)：38-40. (in Chinese)

[4] 何樵登.地震勘探原理和方法[M].北京：地质出版社，1986.

HE Jiao-deng.Principles and method of seismic exploration[M]. Beijing: Geological Publishing House，1986. (in Chinese)

[5] 周博，谢东来，张宪海，等. MATLAB科学计算[M].北京:机械工业出版社,2010.

ZHOU Bo，XIE Dong-lai，ZHANG Xian-hai，et al. MATLAB scientific calculating[M].Beijing: Mechanical Industry Press,2010.(in Chinese)

[6] 曹务祥.检波器组合问题分析[J].石油物探，2008， 47(5):505-510.

CAO Wu-xiang.Detector combination analysis[J].Oil Exploration，2008，47(5):505-510. (in Chinese)

[7] 付彬.地面运动目标地震动信号的模拟技术研究[D].南京：南京理工大学，2004.

FU Bin. Research on the simulation technology of ground moving target vibration signal[D].Nanjing:Nanjing University of Technology and Engineering，2004. (in Chinese)