固体电枢轨道炮非理想电接触的热效应分析

巩 飞，翁春生

(南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094)

在固体电枢轨道炮的发射系统中，电枢与导轨保持滑动电接触，电接触提供电连接，允许输入电流连续地通过接触界面。为了方便数值模拟，大多数的轨道炮发射模拟均假设滑动电接触面为理想接触面，而实际上，固体表面的电接触形式为离散的斑点接触，电流流经接触斑点时产生的收缩效应会导致接触面局部产生额外的温升[1]。因此，不论是在电枢静态或者动态的情况下，接触面的热效应对非理想电接触有着重要的影响作用。

电接触面过高的温升会造成电枢局部烧蚀，电接触由金属-金属接触转变为电弧接触，引起接触转捩。转捩现象对电枢、导轨产生极大的电弧烧蚀，并使接触面受力失去平衡而破坏发射部件在炮膛内的稳定性[2]。为了保持良好的滑动电接触，避免接触转捩的发生，固体接触表面的电接触问题成为近年来研究的热点[3-4]。B. K. Kim等人[5-6]建立了非理想电接触面的三维有限元模型，采用有限元编码EMAP3D，对非理想表面的电扩散及热效应进行了数值模拟。M. Coffo等人[7]通过实验测量给出了接触电阻的经验值，采用有限元编码ANSYS模拟了非理想接触表面的电流分布及热效应。K. T. Hiseh等人[8]建立了两种计算模型，接触表面热通量模型(在B. K. Kim的模型基础上考虑了接触面压力的分布)和接触电阻层模型，通过有限元编码EMAP3D进行模拟，分析了接触表面压力对非理想接触面电流密度及温度分布的影响。国内对于固体电枢轨道炮的数值模拟多采用假设理想电接触面的简化模型，关于非理想电接触面的研究还比较少[9-12]。

本文建立了静态二维非理想电接触的数值计算模型，与之前国外学者均使用有限元编码进行模拟不同，采用有限差分法编写程序，模拟出非理想电接触表面的温升过程，并分析接触电阻层厚度以及材料电导参数随温度变化特性对接触表面热效应的影响作用。

1 研究对象

图1为轨道炮二维几何结构示意图，其中虚线部分为计算区域。假设电枢处于静止状态，电流由一侧导轨流入，经过电接触面、 电枢，从另一侧导轨流出。导轨与电枢材料均选择铜，导轨宽5 mm，电枢为块状电枢，长10 mm、宽10 mm。由于几何结构的对称性，模拟时选取一半区域作为研究对象。

图2(a)表示电枢-导轨电接触面的真实接触形式。实际电接触表面以离散的斑点接触，形成接触区域，实际接触面积远小于名义上的接触面积。当电流流经接触斑点时会产生电流收缩效应，导致接触区域的电阻高于金属主体的电阻，在接触面处产生接触电阻热。图2(b)表示数值模拟的电接触形式。由于接触斑点的随机分布特性及其几何结构的复杂性给数值模拟带来了很大的困难，因此，假设接触区域为一连续的接触表面，通过给出该接触表面产生的额外的热源，模拟出非理想接触面的热作用。

2 计算方法

2.1 控制方程

考虑材料电导率随温度的变化，通过麦克斯韦方程组可得到静态条件下的磁扩散方程[13]：

(1)

式中:B为磁感应强度；σ为电导率；μ0为真空磁导率；T为温度。如果设电导率为常数，方程右侧第2和第3项为0。

给出电导率随温度变化公式如下：

(2)

式中:σ0为初始温度下的电导率；α为电阻温度系数；T0为初始温度。

静态电枢以及导轨中的热传导方程如下：

(3)

式中:k为热导率；ρ为材料密度；c为比热。

磁扩散方程与热传导方程均为抛物型偏微分方程，选用Peaceman-Rachford(P-R)有限差分格式进行计算[9]。该格式为交替方向隐格式，分两步计算，无条件稳定，具有二阶精度，每步需要采用追赶法求解三对角矩阵。

考虑电枢-导轨非理想电接触，根据直流接触电阻的定义可以计算出接触电阻如下：

(4)

式中:Rc为接触电阻；ρa为接触表面两侧材料的平均电阻率；lc为接触电阻层厚度；Ac为实际接触面积。

由接触电阻可以计算出其产生的热流密度qc如下：

qc=ρaJ2lc

(5)

2.2 定解条件

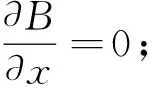
3 计算结果及分析

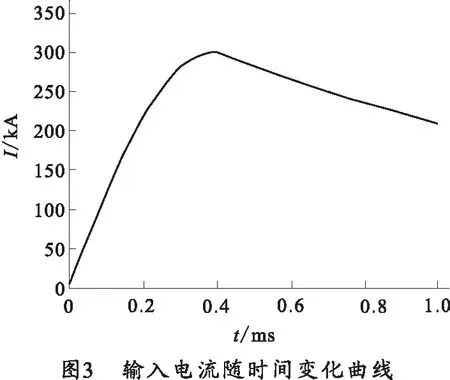
图3给出了外部输入电流随时间变化曲线。在初始阶段，电流迅速增大，0.4 ms内迅速升高到峰值300 kA，随后电流开始缓慢下降，1 ms时衰减到209 kA。

首先，假设电导率为常数，忽略其随温度的变化特性，模拟非理想电接触面的表面温升过程。图4为电接触面温度峰值随时间的变化曲线。计算采用了3种不同的接触电阻层厚度，分别为60、80、100 μm，图中lc=0的曲线表示理想接触面。计算结果表明，非理想接触的表面温升明显高于理想接触，接触电阻层厚度越大，接触面温度峰值越高。由于接触电阻层厚度与接触面压力成反比，因此，提供足够的接触面压力能减小接触电阻热效应。将非理想与理想接触面温度峰值的差值定义为温差。图5为不同接触电阻层厚度下的瞬态温差曲线。从图中可以看出，在0.4 ms时(即输入电流达到峰值时)温差达到最大。结合图4分析，在0.4 ms时理想接触面温度峰值为434.8 K，与理想接触相比非理想接触面(接触电阻层厚度分别为60、80、100 μm条件下)温度峰值分别提高了16.5、21.2、25.9 ℃，提高比率分别达到3.7%、4.8%、5.9%。

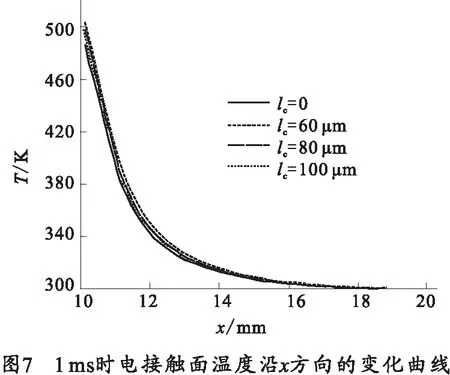
图6为1 ms时轨道炮温度分布图，其中图6(a)为非理想接触，接触电阻层厚度为100 μm，图6(b)为理想接触。计算结果表明，不同接触条件下温度峰值均出现在电枢与导轨接触的尾部区域，且在电枢及导轨内部以水波状向四周递减。在非理想与理想接触下，电枢内部温度峰值分别为476.4、462.5 K，温度提高了3.0%；导轨内部温度峰值分别为483.5、477.2 K，温度提高了1.3%。由于导轨温度峰值出现在临近接触面尾部的区域而非接触面处，因此，其温升作用没有电枢明显。图7为1 ms时电接触面温度沿x方向的变化曲线。从图中可以看出，非理想接触主要对接触面尾部区域的温度影响较大，远离该区域的温度无明显差异。这是由于在电流趋肤效应的作用下，电流向金属表面集中，在计算时间内电流趋肤深度有限，电流主要集中在接触面的尾部区域。图中3种接触电阻层厚度的计算曲线较为接近，在尾部端点处彼此间的温差在3℃左右。

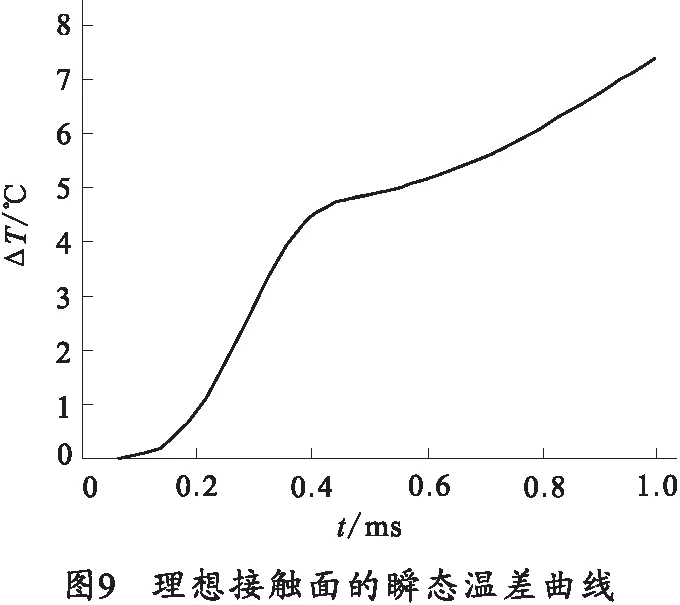
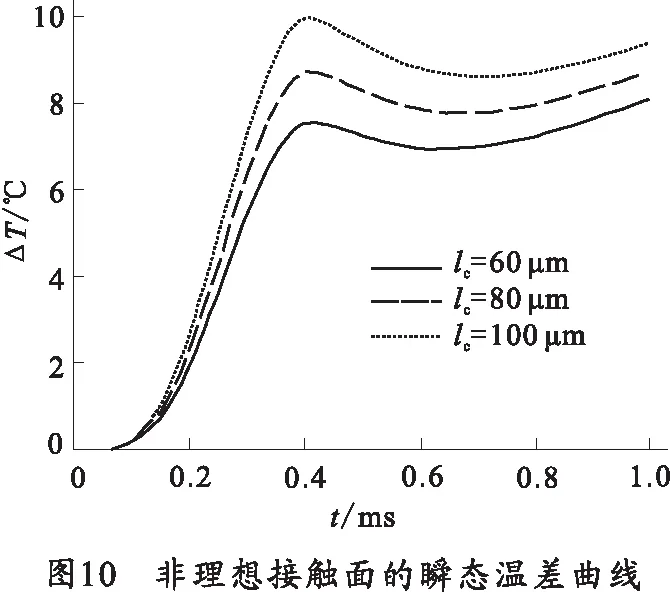
其次，考虑材料电导率随温度变化的特性，分析电导参数变化引起的额外温升。图8为计算中采用的铜的电导率随温度变化曲线。将考虑非定常与定常电导率计算的温度峰值的差值定义为温差。图9为理想接触面的瞬态温差曲线。计算结果表明，电导参数降低会提高电接触面的温度峰值。在初始阶段，由于输入电流较低，接触面温度变化很小，温差接近零；随着输入电流的增大，温差迅速上升，0.4 ms时达到4.6℃，随后受输入电流下降的影响，温差上升变缓；在后期阶段，温差稳定增长，1 ms时达到7.5℃，电接触面温度峰值提高了1.6%。图10为非理想接触面的瞬态温差曲线。从图中可以看出，初始阶段温差变化规律与理想接触相似，0.4 ms时不同接触电阻层厚度(60、80、100 μm)的温差分别为7.3、8.4、9.6 ℃；0.4 ms后，在输入电流降低的作用下，温差出现下降，且随着接触电阻层厚度的增大，下降持续时间越长，1 ms时温差分别达到7.8、8.4、9.1℃，电接触面温度峰值分别提高了1.6%、1.7%和1.9%。

4 结 论

建立了包含接触电阻的二维固体电枢轨道炮热效应的计算模型，采用有限差分P-R算法对静态块状电枢及导轨的电磁场、温度场进行耦合计算，得到了电接触表面温升的变化特性，分析了接触电阻层厚度及材料电导参数的变化对接触表面温升作用的影响。研究结果表明：

1) 接触电阻的存在会在接触表面产生接触电阻热，该效应将导致接触表面温升高于理想接触面，温度提高比率(lc=60、80、100 μm条件下)达到4%～6%左右。

2) 接触电阻层厚度越大，表面温升越快，由于该厚度值由接触面压力决定且与压力成反比，因此预期提高接触面压力，降低接触电阻层厚度，可以减小非理想接触引起的额外温升作用。

3) 在电流趋肤效应的作用下，电流向金属表面集中，计算结果显示，非理想电接触的影响范围主要集中在接触面的尾部区域，接触面头部区域无明显温升作用。

4) 考虑材料电导率随温度的变化特性，电导率的降低会提高单位时间电接触面的焦耳热密度，从而在接触表面处引起额外的温升作用，理想接触表面温度峰值提高比率为1.6%，非理想接触提高比率接近2%。

综合考虑非理想电接触以及材料参数的温度变化特性，可以更加准确的模拟轨道炮在发射过程电接触面的温升过程，为预测接触转捩现象的发生、提高发射效率提供了理论依据。

[1] TIMSIT R S. Electrical conduction through small contact spots[J]. IEEE Transactions on Components and Packaging Technologies, 2006, 29 (4): 727-734.

[2] STEFANI F, LEVINSON S, SATAPATHY S, et al. Electrodynamic transition in solid armature railguns[J].IEEE Transactions on Magnetics, 2001, 37 (1): 101-105.

[3] ROGEON P, RAOELISON R, CARRE P, et al. A microscopic approach to determine electrothermal contact conditions during resistance spot welding process[J]. Journal of Heat Transfer, 2009, 131 (2): 022101.

[4] CHEN W W, WANG Q J, KIM W. Transient thermomechanical analysis of sliding electrical contacts of elastoplastic bodies, thermal softening, and melting inception[J]. Journal of Tribology, 2009, 131 (2): 021406.

[5] KIM B K, HSIEH K T. Numerical study of electric diffusion effect due to imperfect electrical contacts[J]. IEEE Transactions on Magnetics, 1998, 34 (4): 1249-1251.

[6] KIM B K, HSIEH K T, BOSTICK F X. A three-dimensional finite element model for thermal effect of imperfect electric contacts[J]. IEEE Transactions on Magnetics, 1999, 35 (1): 170-174.

[7] COFFO M, GALLANT J. Simulation of the current distribution and the heat load of a brush projectile in a railgun with the finite element code ansys[J]. Acta Physica Polonica-Series a General Physics, 2009, 115 (6): 1112-1114.

[8] HSIEH K T, SATAPATHY S, HSIEH M T. Effects of pressure-dependent contact resistivity on contact interfacial conditions[J]. IEEE Transactions on Magne-tics, 2009, 45 (1): 313-318.

[9] 李昕, 翁春生. U型电枢非稳态电磁场二维数值模拟[J]. 火炮发射与控制学报, 2009(1): 1-4.

LI Xin, WENG Chun-sheng. Two-dimensional numerical simulation of unsteady electromagnetic field in u-shaped solid armature[J]. Journal of Gun Launch & Control, 2009(1): 1-4. (in Chinese)

[10] XIA Sheng-guo, HE Jun-jia, CHEN Li-xue, et al. Studies on interference fit between armature and rails in railguns[J]. IEEE Transactions on Plasma Science, 2011, 39 (1): 186-191.

[11] YU Xin-jie, FAN Zhao-nan. Simulation and two-objective optimization of the electromagnetic-railgun model considering vsec resistance and contact resistance[J]. IEEE Transactions on Plasma Science, 2011, 39 (1): 405-410.

[12] 陶青青, 吕庆敖, 李鹤, 等. 轨道推进器瞬态电磁场有限元分析[J]. 火炮发射与控制学报, 2011(1): 54-56.

TAO Qing-Qing, LV Qing-Ao, LI He, et al. Finite element analysis of electromagnetic rail launchers[J]. Journal of Gun Launch & Control, 2011(1): 54-56. (in Chinese)

[13] POWELL J D, ZIELINSKI A E. Ohmic heating in a double-taper sabot-armature[J]. IEEE Transactions on Magnetics, 2009, 39 (1): 153-157.