某迫击炮炮口流场数值模拟与分析

黄 欢，何 永，蔺月敬

(南京理工大学 机械工程学院，江苏 南京 210094)

迫击炮是一种运动性和弹道机动性良好的火炮，和同口径的一般火炮相比，具有体积小、质量小、使用和携带方便等优点。它们能在第1线步兵的战斗队形内行动，对部队的火力要求反应迅速，及时、准确和猛烈的火力支援步兵完成战斗任务。在发射过程中，根据迫击炮人体工学，战士须靠近迫击炮操作。因此，其炮口流场引起的超压值对人体的影响是迫击炮研究的重点和难点[1]。

国内外学者对迫击炮炮口流场的早期研究计算主要是建立在实验基础上，采用一维近似算法。随着计算流体力学的发展，炮口流场的计算有了很大的进展[2]。本文采用考虑炮膛与弹丸定心部间隙造成气体流失的内弹道过程，以及考虑后效期火药气体与弹丸的耦合作用，对迫击炮膛内气体建立二维轴对称雷诺平均N-S方程，使用S-A单方程湍流模型，采用Roe的一阶迎风格式[3-4]，应用动网格技术数值模拟了迫击炮膛内及炮口流场，研究结果对迫击炮炮口流场特性的研究有重要意义。

1 炮口流场数学模型

1.1 控制方程

考虑到迫击炮发射过程的复杂性，提出如下假设：

1)忽略火药气体多组分和化学反应的影响，将其与外界大气看视为同一气体介质，完全服从气体状态方程。

2)采用内弹道过程的计算结果对炮口流场模拟过程进行初始化。

3)炮口流场模拟过程为弹丸出炮口至后效期结束。

1.1.1 Naiver-Stokes方程

根据以上假设，建立炮口流场二维轴对称雷诺平均N-S方程：

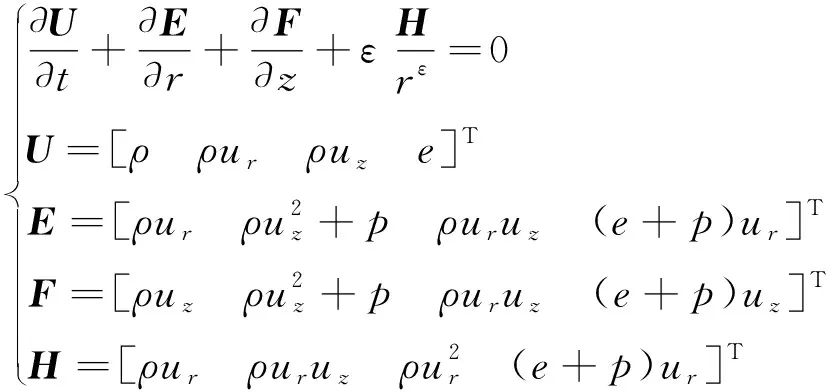
(1)

式中：ρ为火药气体密度；ur为火药气体径向流速；uz为火药气体轴向流速；e为火药气体单位比内能；p为压强;ε为湍能耗散率。

1.1.2 湍流控制方程

本文采用Spalart-Allmaras方程湍流模型(S-A模型)。S-A模型用于求解动力涡粘性输运方程的相对简单的一种模型，不必去计算和局部剪切层厚度相关的长度尺寸，应用在较粗的壁面网格时也取得了较好的结果。单方程在湍流时均的连续性方程与雷诺方程的基础之上，再建立一个湍动能k的运输方程，将湍流粘度μ表示成k的函数，从而使方程组封闭。湍动能的运输方程为：

(2)

从左至右，方程(2)中各项依次为瞬态项、对流项、扩散项、产生项。由普朗特表达式有[5]：

(3)

式中：σk、CD、Cμ为经验常数，σk=1，Cμ=0.09，CD=0.08～0.38。

在网格运动条件下，流场内控制体发生改变，采用有限容积法来表示守恒方程：

(4)

式中：ρ为火药气体密度；φ为通用变量；u为火药气体速度矢量；ug为运动网格速度矢量；Γ为扩散因子；S为源项；A表示控制体积的边界。

1.2 计算区域网格划分方法

考虑到后效期弹丸和火药气体的流固耦合作用，采用结构化网格动态层变技术。根据紧邻运动边界网格层高度的变化，添加或者减少动态层。

动态分层模型思想：

h≥(1+αs)hideal

(5)

h≤αchideal

(6)

当动边界拉伸毗邻网格层满足(5)式时，就可以对网格层进行分割；当动边界压缩毗邻网格层满足式(6)时，两网格层合并为一层。hideal为理想单元高度，本文取6mm。αs为层的分割因子，本文取0.4。αc为层的合并因子，本文取0.04。该方法模拟过程耗时少，同时结合分块网格技术对炮口流场进行数值模拟。

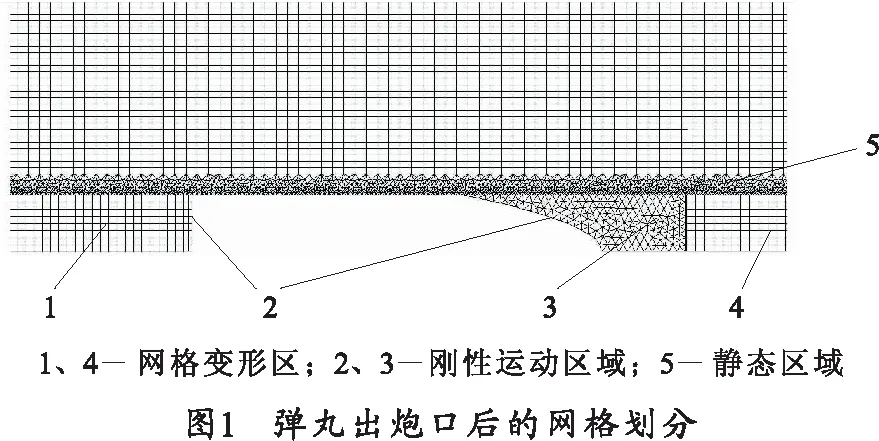
以下为计算区域分块网格的划分方法。图1为弹丸出炮口后的网格划分。如图1所示，对炮口流场区域划分为网格变形区1与4，刚性运动区域2与3，静态区域5。刚性运动区域的运动通过编程定义，运用牛顿第二定律计算火药气体作用弹丸运动。此区域在运动过程中，分别使网格变形区域1与4网格层分裂与合并。静态区域5与1、2、3、4数据传输时，须对5用非结构化网格加密，以免在数据传输过程中出现数据间断，影响迭代收敛和等值线图。同时由于使用动态分层法，使得结构化网格改变均匀，易于计算。图中弹丸为迫击炮弹丸简化模型，弹丸定心部为平面弹底。目的是使弹丸影响的炮口流场更加恶劣复杂，提高研究超压值的安全性。

2 膛内过程计算

2.1 考虑炮膛与弹丸定心部间隙的内弹道模型

考虑到迫击炮发射过程膛内现象的复杂性，提出以下假设：

1)弹丸在膛内运动时，不考虑弹前阻力。

2)膛壁的导热系数为零。

3)燃气与未燃尽的固体颗粒在弹后整个空间均匀分布，即认为每一断面的质量密度都相等，从而可以得出气流速度从膛底为零到弹底的与弹丸相同的运动速度之间呈线性分布。

4)考虑因炮膛与弹丸定心部间隙造成的流失现象。

5)忽略身管后坐和膛内压力波的反射、传递等造成的影响。

基于上述假设，采用某口径迫击炮的经典内弹道数学模型，通过四阶龙格-库塔法获得弹丸出炮口时内弹道参数。考虑炮膛与弹丸定心部间隙的影响，火药气体随着弹丸运动不断从间隙流出，气体相对流失量[6]：

(7)

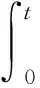
考虑间隙影响的膛内平均压力计算公式为：

(8)

式中：f为平均火药力；ψ为火药装药烧去的百分比；θ为气体混合物比热比；mv2/2为弹丸动能；l为弹丸行程；lψ为药室自由容积缩颈长。

同时通过形状函数、燃速方程、弹丸运动方程以及能量方程获得弹丸出炮口时内弹道参数。

2.2 膛内过程计算结果

计算的迫击炮由于膛压低、初速小、装药量小及药室容积大，因此装填密度很小。为保证点火均匀和提高射击精度，采用变装药结构，火药是燃速大的薄火药。在此装填条件下，全装药的燃烧结束时间几乎和最大压力位置重合。

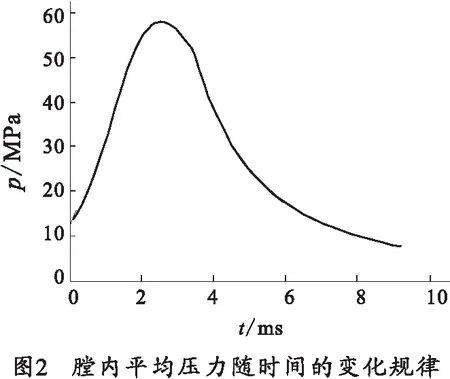
图2为膛内平均压力随时间的变化规律。内弹道计算获得膛底最大压力为58.48 MPa。试验测得铜柱压力52.4 MPa,修正得膛底最大压力58.24 MPa。

考虑弹丸定心部与膛壁之间间隙的影响，计算出火药气体相对流失量与时间的关系，如图3所示。当火药燃烧结束时刻，相对流失量η为12.3%；弹丸出炮口时刻，相对流失量η达21.3%。由此可见，相对流失量是滑膛迫击炮设计的一个重要参数。

图4为弹丸速度随时间的变化规律，弹丸在膛内运动时间为9.2 ms。在即将出炮口时，速度变化已经趋于平缓，计算获得弹丸初速为324.8 m/s。测得初速为324 m/s。试验结果与计算结果吻合，从而验证了迫击炮内弹道过程计算的合理性，计算结果将用于炮口流场数值模拟的参数初始化。

2.3 弹丸出炮口时内弹道参数初始化

由考虑间隙的内弹道计算获得弹丸出炮口时刻的弹底速度、膛内平均压力，通过求解热力学方程获得膛内平均温度[6]。由假设(3)可知，此时膛内气体流动速度呈线性分布如式(9)。同时通过弹底压力及平均膛压之间的关系获得弹底压力，再通过式(10)得出此时膛内压力分布[7]。膛内温度取平均温度。依据参数分布，初始化弹丸出炮口时的炮口流场。

(9)

式中：ux为膛内气体径向速度；v为弹底速度；L为膛底至弹底的距离。

(10)

式中：px为膛内气体压力；pd为弹底压力；φ1为次要功系数，本文取1。

数值模拟的某口径迫击炮弹丸初速小、膛压较低，炮口流场仿真总时间为4 ms。弹丸质量为4.2 kg。CFL数取0.8。计算时间步长为0.001 ms。

3 炮口流场模拟结果与分析

弹丸飞离迫击炮炮口后，由于膛内高压火药气体高速喷出，在炮口周围会产生一个不断向外传播的炮口冲击波，以及产生一个相对来说稳定在炮口的超音速射流结构。弹丸刚出炮口时，高温高压气体首先从弹尾部溢出，向侧方剧烈膨胀，形成一个近似球形且球心运动的冲击波，此为炮口冲击波。而超音速射流结构是一个由正激波与斜激波系形成边界的区域，在此区域内气体产生主膨胀和冷却。图5为弹丸出炮口后2 ms时的炮口静压场。释放的火药气体由于直接气流的干涉产生，在弹丸后方引起一个强激波。这一激波最后变成半稳态正激波，并带有斜激波，形成射流的中心超声速区，称为“激波瓶区”。

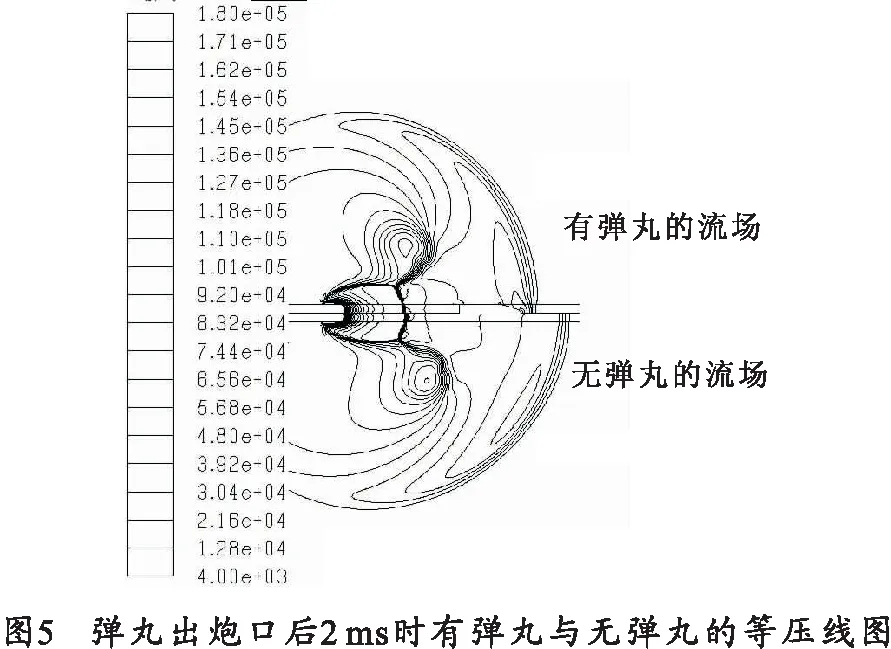
由图5可知，在有弹丸的情况下激波瓶区与无弹丸的情况形成基本相同。但是，从图5中压力等值线可以看出，弹丸的存在阻碍了火药气体的扩散，提高了炮口冲击波的强度。因此，考虑弹丸运动影响的炮口流场使模拟结果更加符合实际情况。

炮口冲击波为强压缩波，近似球状向四周扩大，提高周围压力，造成超压现象。为研究迫击炮炮口流场超压值对人体的影响，在炮口处建立a、b、c3个监测点，如图6所示。a点与b点连线与身管平行。

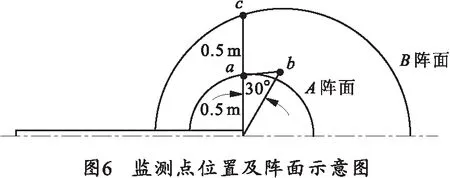
通过数值模拟获得在弹丸出炮口后4 ms内此3点压力变化曲线，如图7所示。

由于炮口冲击波球状扩大，同时球心向前运动的速度不断衰减且小于球体膨胀速度。由图6中A阵面所示，炮口冲击波波面几乎同时经过a点与b点，两点到达静压峰值时刻相近,a为0.94 ms,b为1.04 ms。炮口冲击波是一个各向异性的非均匀冲击波。根据波后波前之压力比和来流马赫数之间的关系可知[8]，冲击波波面上的压力并非均匀，其值从球右至左递减。因此，a点超压值小于b点超压值。c点远离冲击波球心，所以其超压值出现时间也在a点与b点之后，处于B阵面上,c点为2.34 ms。炮口冲击波由火药气体连续地、有限的补充能量。由于膛内火药气体向外排出的速度随时间呈指数规律衰减，向炮口冲击波补充的能量也不断递减。所以随着炮口冲击波的扩大，其压缩气体造成超压的能力不断变小。因此，c点超压值较小。模拟结果中a点超压值32.9 kPa,b点超压值63.4 kPa,c点超压值12.6 kPa。根据炮口冲击波对人员内脏损伤的安全限值可计算出炮口安全范围。

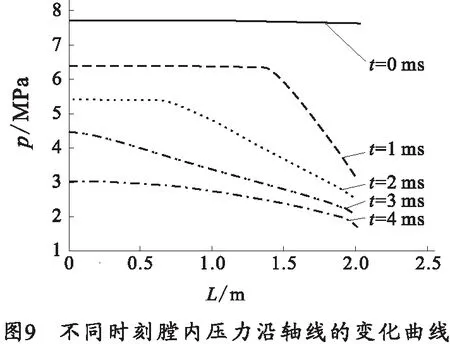
数值模拟过程中假设身管热传导率为0，气体黏度取空气黏度，因此在极短时间内气体流失在膛内部分可近似等熵过程。由图8和图9可知，膛内压力与温度变化较为相似，符合在等熵过程中两者的关系。随着膛内气体不断膨胀，膛内压力与温度不断下降。膛内气流速度初始时刻呈线性分布，在膛口处最大。因此，靠近膛口处压力与温度比靠近膛底处的下降速度快。当t=4 ms时，膛内的压力与温度下降速度较为均匀。

4 结 论

通过计算流体力学方法，考虑了弹丸出炮口时火药气体与弹丸的相互作用，对某型迫击炮炮口流场特性进行了数值模拟，计算结果表明：

1)弹丸出炮口时刻，弹丸定心部与膛壁之间间隙造成的相对流失量达21.3%，是迫击炮内弹道计算及炮口流场分析的重要影响因素。

2)引入了火药气体与弹丸运动的耦合作用，炮口冲击波数值研究更加符合实际。

3)不同监测点超压值的分析对安全区域的确定提供理论依据。a点与b点的比较说明，离炮口越后，超压值越小；a点与c点的比较说明，离炮口越远，超压值越小。

4)得到的膛内气体流空过程膛内温度压力参数变化，对研究炮口冲击波的形成及身管温升问题有指导意义。

研究未模拟弹丸膛内运动，难以解决初始冲击波对炮口流场的影响。

[1] 樊孝才.迫击炮设计[M].北京：国防工业出版社，1982：5-6.

FAN Xiao-cai. Mortars design[M]. Beijing：National Defence Industry Press, 1982：5-6. (in Chinese)

[2] 郁伟，朱斌，张小兵.耦合内弹道过程的膛口流场数值模拟与分析[J].南京理工大学学报,2009,33(3)：335-338.

YU Wei，ZHU Bin, ZHANG Xiao-bing. Numerical simulation and analysis of muzzle flow field coupling with interior ballistic process[J]. Journal of Nanjing University of Science and Technology, 2009,33(3)：335-338. (in Chinese)

[3] 王仕松,郑坚，贾长治，等.带制退器的膛口流场数值模拟[J].火力与指挥控制，2011,36(2):148-151.

WANG Shi-song， ZHENG Jian, JIA Chang-zhi, et al. Numerical simulation of muzzle blast flow field with muzzle brake[J]. Fire Control&Command Control, 2011,36(2):148-151. (in Chinese)

[4] 江坤,王浩.基于动网格技术的膛口流场数值模拟[J].火炮发射与控制学报,2010(3):1-4.

JIANG Kun，WANG Hao.Numerical simulation of muzzle flow fieId based on dynamic meshing technique[J].Journal of Gun Launch&Control,2010(3):1-4.(in Chinese)

[5] 朱红钧.FLUENT流体分析及仿真实用教程[M].北京：人民邮电出版社，2010:106-107.

ZHU Hong-jun.FLUENT fluid analysis and simulation practical tutorial[M].Beijing：Posts and Telecom Press, 2010:106-107. (in Chinese)

[6] 钱林方.火炮弹道学[M].北京：北京理工大学出版社,2009:166-168.

QIAN Lin-fang.Artillery ballistics[M].Beijing：Beijing Institute of Technology Press,2009:166-168.(in Chinese)

[7] 张柏生.火炮与火箭内弹道原理[M].北京：北京理工大学出版社,1996：78-80,150-151.

ZHANG Bo-sheng. Interior ballistic principle of artillery and rockets[M]. Beijing：Beijing Institute of Technology Press, 1996:78-80,150-151. (in Chinese)

[8] 高树滋，陈运生.火炮反后坐装置设计[M].北京：兵器工业出版社，1995:293-294.

GAO Shu-zi,CHENG Yun-sheng.Artillery recoil mechanism design[M].Beijing：Weapon Industry Press,1995:293-294. (in Chinese)