基于CFD的两栖车辆阻力计算与预报研究
2012-11-23郭张霞李魁武潘玉田傅宇雁
郭张霞,李魁武,潘玉田,傅宇雁
(1.中北大学, 山西 太原 030051;2.西北机电工程研究所,陕西 咸阳 712099;3.西安现代控制技术研究所,陕西 西安 710065)
1 计算方法
快速性是两栖车辆诸性能中的重要性能之一,对两栖车辆而言,快速性与提高战斗力和生存能力密切相关。因此,两栖车辆设计中的关键技术之一就是预报和优化设计武器的快速性。而两栖车辆快速性包含阻力和推进两方面,研究车辆航行中的阻力问题对改善其快速性具有重要作用。
两栖车辆阻力的确定长期以来都停留在水池模型阻力试验的基础上,不但耗费大量的人力物力,而且对车辆周围的流场不能精确描述。因此,在两栖车辆的设计阶段,采用CFD的方法无疑是比较理想的选择。
两栖车辆与船舶构型差别显著,其特点是长度小,表面积小和形状变化突出,其中车辆的负重轮、履带等行动装置即成为这些部分的主体。因此,船舶理论中有关航行阻力的分析方法对两栖车辆已不甚适用,而在两栖车辆的航行总阻力中,航行阻力的构成比例和量值也与船舶很不相同[1]。
两栖车辆的航行阻力主要由摩擦阻力、形状阻力和兴波阻力组成,摩擦阻力与水的粘性有关;形状阻力与水的粘性和水的压力有关;兴波阻力与车速有关[2]。对于进行水池试验的拖模来讲,要让它和实车同时满足雷诺数和傅汝德数相等也是不能实现的。因此,只能在保证傅汝德数相等的情况下进行试验。为了能从拖模试验结果中求得实际的阻力,傅汝德作了如下假定:假定两栖车辆的航行阻力分为两部分,一部分是摩擦阻力,可以按1957年ITTC相当平板公式计算,只与雷诺数有关;另一部分称为剩余阻力(包括兴波阻力和形状阻力),符合傅汝德相似准则,即对应的无因次阻力系数相等,只与傅汝德数有关[3]。
两栖车辆采用傅汝德二因次法换算的总阻力可以用下述形式表达:
剩余阻力系数Cr=Ctm-Cfm
实车总阻力系数Cts=Cfs+Cr+ΔCF
总阻力Fts=Cts×(ρSv2/2)
式中:Cts为实车总阻力系数;Cfs为实车摩擦阻力系数;Cr为剩余阻力系数;ΔCF为模型与实车之间阻力换算的补偿值,一般取0.004;Ctm为拖模总阻力系数;Cfm为拖模摩擦阻力系数;Rts为实车总阻力;ρ为水密度;S为湿表面积;v为航速。
这样通过CFD数值模拟可以计算出模型的剩余阻力,从而求得剩余阻力系数Cr,通过相应的经验公式可以得出Cfs,进而求得总阻力系数Cts,利用阻力系数和阻力的关系可算出总阻力。
2 数学模型
2.1 控制方程
不可压缩流体连续性方程和N-S方程[4]:

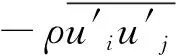
自由面的波动是采用VOF方法来追踪的,其方程可写为:
a1+a2=1
其中a1、a2分别为空气相、水相的体积分数。
2.2 湍流模型
文中对两栖车辆航行阻力的计算采用k-ε湍流模型。其湍流动能k方程为[5-6]:
Gk+Gb-ρε-YM+Sk
湍流耗散率ε方程为:
式中:Gk为由于平均速度梯度引起的湍动能产生;Gb为由于浮力影响引起的湍动能产生;YM为可压缩湍流脉动膨胀对总的耗散率的影响。μt表示湍流粘性系数,作为常数,C1ε=1.44,C2ε=1.92,C3ε=0.99。
2.3 边界条件
这是一个气液两相流动问题,由于两栖车辆上部为空气、下部为水,在航行过程中必然引起水与空气之间的相互作用,并产生波浪。波浪理论大致可分为线性波和非线性波两类。在实际海况中,波浪的波高相对于波长(或相对于水深) 一般是有限的,在这种有限振幅波中,波动的自由水面引起的非线性影响必须加以考虑,因此,对于实际海洋中的波浪进行研究需要基于非线性波理论。本文采用二阶Stokes波浪,入射边界处的速度满足以下条件:
x方向速度:
y方向速度:
式中:H为波高;θ为相位角;L为波长;k为波数;d为不计及波面的水深;s为计及波面的水深;T为周期。
本文利用UDF技术将其作为入射边界条件耦合到计算方程中,从而实现非定常波浪模拟。
此计算域的边界条件分为入口、出口及壁面等,在来流方向的入口边界上给定来流速度、空气和水的体积分数;出口边界远离两栖车辆且流动已达到稳定状态;将与来流方向平行的远方边界设为自由出流边界;考虑到粘性的影响,将车辆表面定义为不可滑移壁面;将计算域底部设为固定边界。
2.4 数值计算方法
采用有限体积法离散动量方程。对流项采用二阶迎风差分格式,扩散项采用中心差分格式,压力速度耦合采用SIMPLE算法。
3 计算模型与结果分析
3.1 两栖车辆拖模试验
试验在某大学船模试验水池进行,水池长160 m,宽7 m,水深3.7 m;拖车为空腹梁结构,速度范围0.01~8 m/s。 供试模型采用钢质模型,全部用2 mm优质冷轧钢板焊接制成,模型缩尺比为1∶4。模型经过防锈处理,加装防浪板及导航板等附件。模型试验的数据如图1所示。
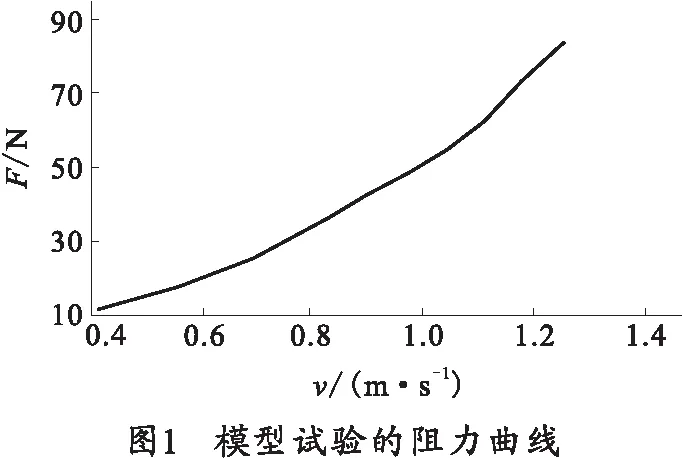
3.2 计算模型建立
实践证明,同结构网格相比,非结构化网格更适合于复杂区域的网格划分,其随机的数据结构更易于作网格自适应,以便更好地捕获流场的物理特性,因此,本计算的计算模型均采用非结构化网格。计算采用的计算模型与模型一致,数值计算流场的长度、宽度和水深分别为160、7、3.7 m(参照了模型试验所在水池的尺寸),图2为两栖车辆模型图。为了简化问题,轮胎用近似圆柱体代替,计算模型按左右对称处理,计算域为车前5倍车长,车体顶部2倍车长。

3.3 计算结果
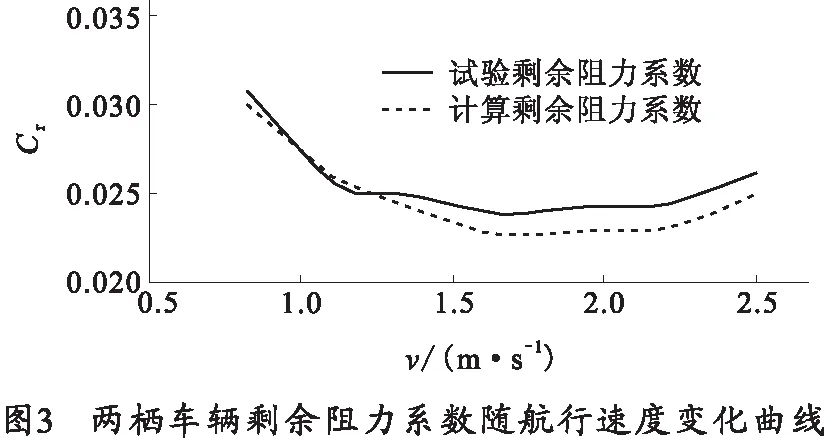
通过一系列的两栖车辆湍流黏性流理论和傅汝德二次因法计算以后,实车总阻力计算结果比较见表1所示,表中ΔCF取0.004,摩擦阻力曲线。图3为两栖车辆剩余阻力系数随航行速度变化曲线,图4为两栖车辆总阻力随航行速度的变化曲线。

表1 两栖车辆实车阻力计算结果

4 结 论
本文利用流体力学理论对两栖车辆航行性能进行了数值模拟,从最终研究结果可以得到如下结论:
1)在湍流黏性理论下,对于剩余阻力系数的比较而言,数值模拟下的计算值与模型试验值基本一致,特别在v≥1.667m/s时剩余阻力系数基本不随航行速度的变化而变化,当v<1.667m/s时,变化率较快。
2)从图4可以看出实车在水中的阻力随航速的增大而增大,这与船舶的阻力特性是吻合的。同时通过比较可以看出计算所得的阻力曲线和试验所得曲线是较吻合的,尤其是在低航速时,计算结果和试验结果吻合得相当好,说明对两栖车辆流场进行数值计算所采用的湍流模型、计算方法和边界条件是合理的。
3) 在目前流场数值计算技术比较成熟的情况下,建议采用数值计算技术和试验技术相结合的手段对两栖车辆阻力进行预报。
[1] 徐国英,刘维平.两栖车辆水阻力构成研究[J].装甲兵工程学院学报,1998(3):59-63.
XU Guo-ying, LIU Wei-ping.Composition of water resistance to amphibious vehicle[J].Journal of Armored Force Engineering Insistute, 1998(3) : 59-63.(in Chinese)
[2] 居乃鵕.两栖车辆水动力学分析与仿真[M].北京:兵器工业出版社,2005.
JU Nai-jun.Hydrodynamics analysis and simulation for amphibious vehicle[M]. Beijing: The Publishing House of Ordnance Industry, 2005.(in Chinese)
[3] 余建伟.基于CFD的船舶阻力计算与预报研究[D]. 上海:上海交通大学,2009.
YU Jian-wei. Research on calculation and prediction for ship resistance based on CFD theory[D]. Shanghai: Shanghai Jiao Tong University, 2009.(in Chinese)
[4] GAROFALLIDIS D. Experimental and numericalinvestigation of the flow arounda ship model at various Froude numbers[D]. Athens: Department of Naval Architecture and Marine Engineering, 1996.
[5] CHOI J E,MIN K S,KIM J H,et al. Resistance and propulsion characteristics of various commercial ships based on CFD results[J]. Ocean Engineering,2010,37:549-566.
[6] 吴颂平,刘赵淼.计算流体力学基础及其应用[M]. 北京:机械工业出版社,2008.
WU Song-ping, LIU Zhao-miao.Computaional fluid dynamics[M]. Beijing:China Machine Press, 2008.(in Chinese)
