稀薄颗粒流体对弯管冲蚀的数值模拟

易卫国,杨 谦,李群松

(湖南化工职业技术学院化工系,中国 株洲 412000)

石油化工生产及其他行业用管道输送流体介质时，流体中的颗粒不可避免的对管道造成冲蚀．其影响因素很多、很复杂，如：流体介质中颗粒的大小、速度等，其危害程度比较大，特别是当工作介质易燃易爆或者有剧毒时，一旦产生事故后果不堪设想．如：我国陕京输气管道琉璃河分输处曾因气源中含较多颗粒、流速过高等原因造成阀门被冲刷穿孔；我国中原油田污水管道和印度输送煤气管道都报道过发生管内壁底部槽沟磨损引起开裂事故等等．因此，我们非常需要比较准确的预测管道中最容易磨损的部位及磨损的速度，以保证管道设备能可靠安全运行．人们对浓度大的颗粒流对管道的冲蚀机理及模拟预测等做了不少的研究[1-6]．但值得一提的是当流体中的颗粒含量不高时，危险是同样存在的[7]，却往往容易让人忽视，文章正是基于这方面的考虑，针对含少量颗粒流体通过管弯时对管壁的冲蚀，以含沙水流为例利用计算机进行了数值模拟，在此，不考虑工作介质对管道的腐蚀作用．

1 模型的建立

1.1 数学模型

管内含沙水流的流动属于典型的固-液两相流,由于所研究的对象是固体颗粒含量小于10%(体积分数)的流体，颗粒显得非常的稀薄，因此可以采用离散相模型．利用拉格朗日法对通过流场的颗粒进行逐个跟踪，再分别计算在各种不同的工况下弯头各部分的磨损量．

1.1.1 液-固两相连续性方程

1.1.2 动量方程

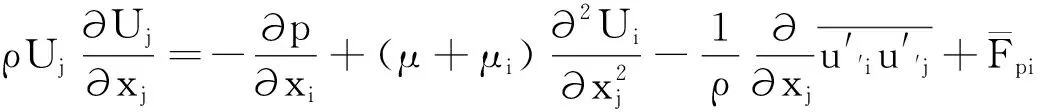
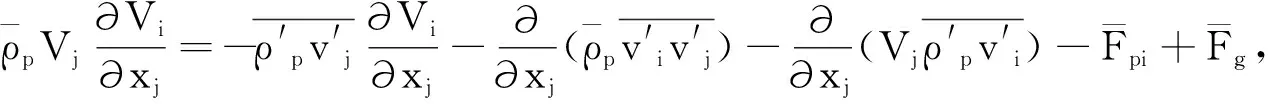
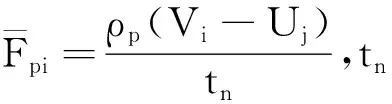
1.1.3k-ε方程

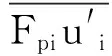
1.1.4 DPM冲蚀模型

1.2 几何模型及网格

模型如图1所示．90°弯头公称直径为100 mm，内直径为89 mm，弯曲半径152 mm，弯头两端各伸出300 mm．含颗粒流体从上端管口以10 m/s的初速度垂直进入．在proe中建立几何模型后，以stp格式导入至gambit中进行网格划分，采用六面体网格单元，最后得到网格数为150 181，如图2所示．

图1 弯头模型 图2 模型网格

2 数值模拟

2.1 前提条件

不考虑流体中沙粒与沙粒相互之间的撞击力作用，认为沙粒大小均匀，密度为1 500 kg/m3，沙粒的质量流量恒定为1 kg/m3，忽略介质对管壁的腐蚀．平均流动是三维、定常、不可压缩、等温流动,湍流的局部各向同性．忽略由于颗粒周围流体存在压力梯度而产生的力、颗粒旋转产生的Magnus力、粘性剪切力．

2.2 计算方法

利用Fluent6.3流体分析软件对弯管内含沙粒水流进行三维数值模拟，采用k-ε标准双方程求解，使用三维隐式分离求解器，控制方程的离散采用有限单元体积法，液-固耦合采用SIMPLE算法．利用拉格朗日法对通过流场的颗粒进行逐个跟踪[8-10]，再分别计算在各种不同的工况下弯头各部分的磨损量，水作为连续相，沙粒作为离散相．

2.3 边界条件

为了便于比较，分两种情况进行模拟．第一种情况：入口速度相同而沙粒直径不等；第二种情况：沙粒直径相同而入口速度不同．每种情况下又分为4种不同的工况．在设置边界条件时，注意边界条件存在差异．

(1)弯管内连续相介质为水，分散相为沙粒．

(2)入口边界条件：流体进口速度Uin见表2．对于完全发展的管流其湍流强度I可以用下面的经验公式计算：湍流强度I=0.16 (ReDH)-1/8, 式中DH为水力直径, 对完全发展的管流,DH=D(D为弯管内直径)，为按水力直径DH计算得到的雷诺数，分别为0.2、0.3、0.4、0.5 mm和15、18、21、24 m/s的情况计算．

(3)流体出口边界条件:设置为Outflow．

3 计算结果及比较

3.1 粒子运动轨迹追踪及冲蚀部位预测

通过300次迭代计算，结果显示各项指标参数均已收敛，得出弯管中沙粒运动轨迹图3及冲蚀示意图4．

图3 单个粒子轨迹 图4 弯管冲蚀部位

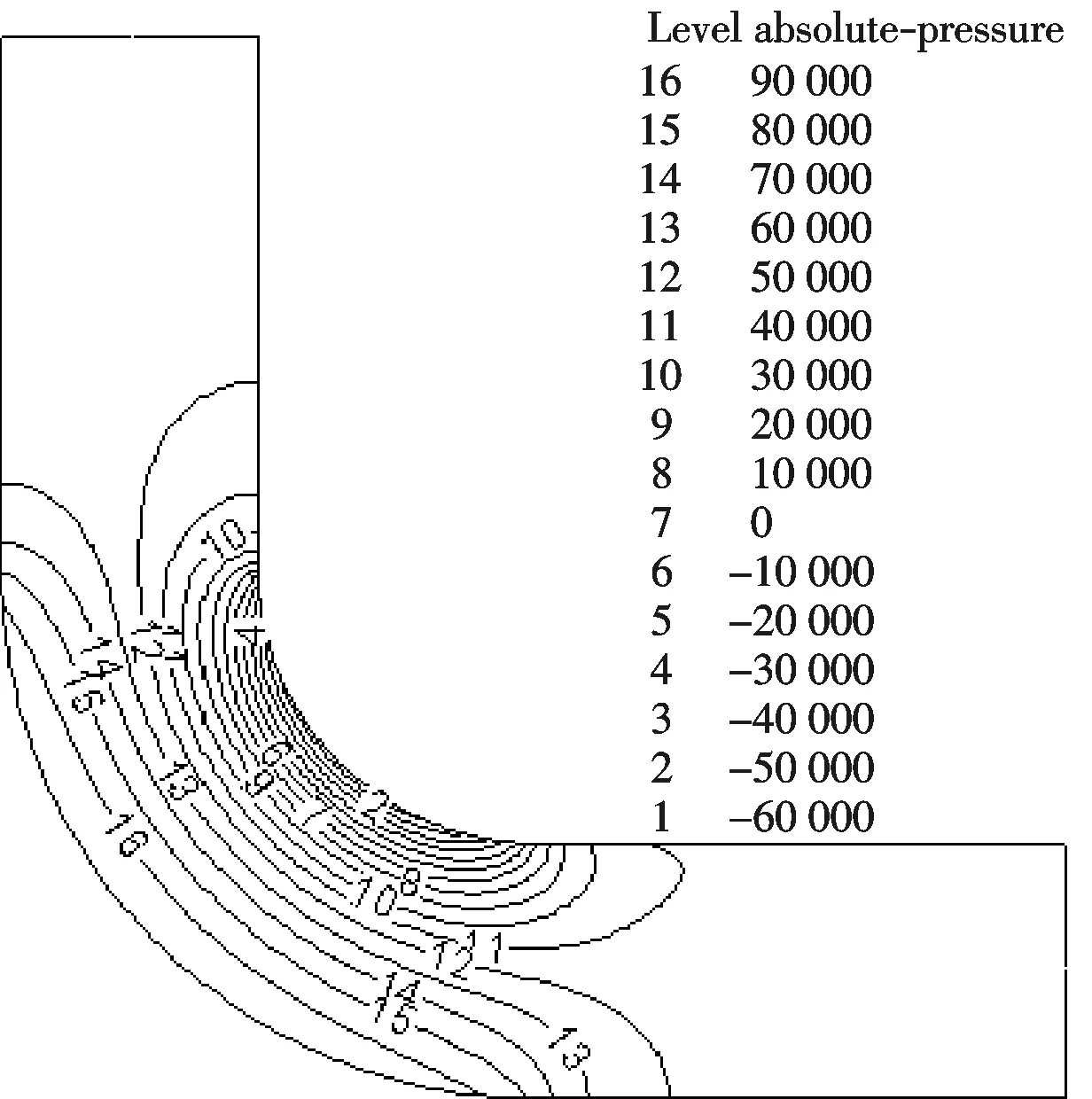
图5 弯头中心截面压力等值线分布

从沙粒的运动轨迹及它对弯管壁面的冲蚀效果来看，发现冲蚀主要发生在弯管的底部内表面，如图4所示．因为当沙粒自入口随流体以一定的速度流入后，由于惯性的作用，沙粒在弯头曲率变化的部位以一定的角度撞击壁面,从而导致了该区域的磨损量较其他部位大．并且冲蚀程度随弯头部位截面的转角α(图1)的增大而增大．

图5为弯管中心截面处的压力等值线图，由图可以看出：弯头外侧压力明显高于内侧，使得水流中的沙粒在弯管外侧密集度增大，而靠近内侧区域由于压力低基本上属于无沙粒区域，这从另一方面验证了为什么弯管冲蚀磨损总发生在弯头的下半部表面．

3.2 颗粒入口速度对冲蚀的影响

在上述几种工况下，将弯头处按图1划分为2段截面(区域A、B)，在Fluent的后处理中再分别对全管壁面、弯头部位(1-1,3-3所包围的区域)、以及A、B段截面进行面积分，就可以得出在不同的工况下每段截面上的平均冲蚀速率的比较图．

图6展示了含沙粒水流在不同的入口速度下，相同直径的沙粒对弯管壁面的冲蚀率．从图5可以看出：当沙粒直径不变化时，入口速度越大，则弯头各部位的冲蚀率呈显著增大的趋势．并且弯头的下半部分B部位的平均冲蚀率远远高于上半部分A部位的平均冲蚀率．这与我们从现场观测到的弯头冲蚀磨损情况是相符的．

图6 相同粒径不同速度下弯头各部分平均冲蚀率比较 图7 相同速度不同直径比较

3.3 颗粒直径对冲蚀的影响

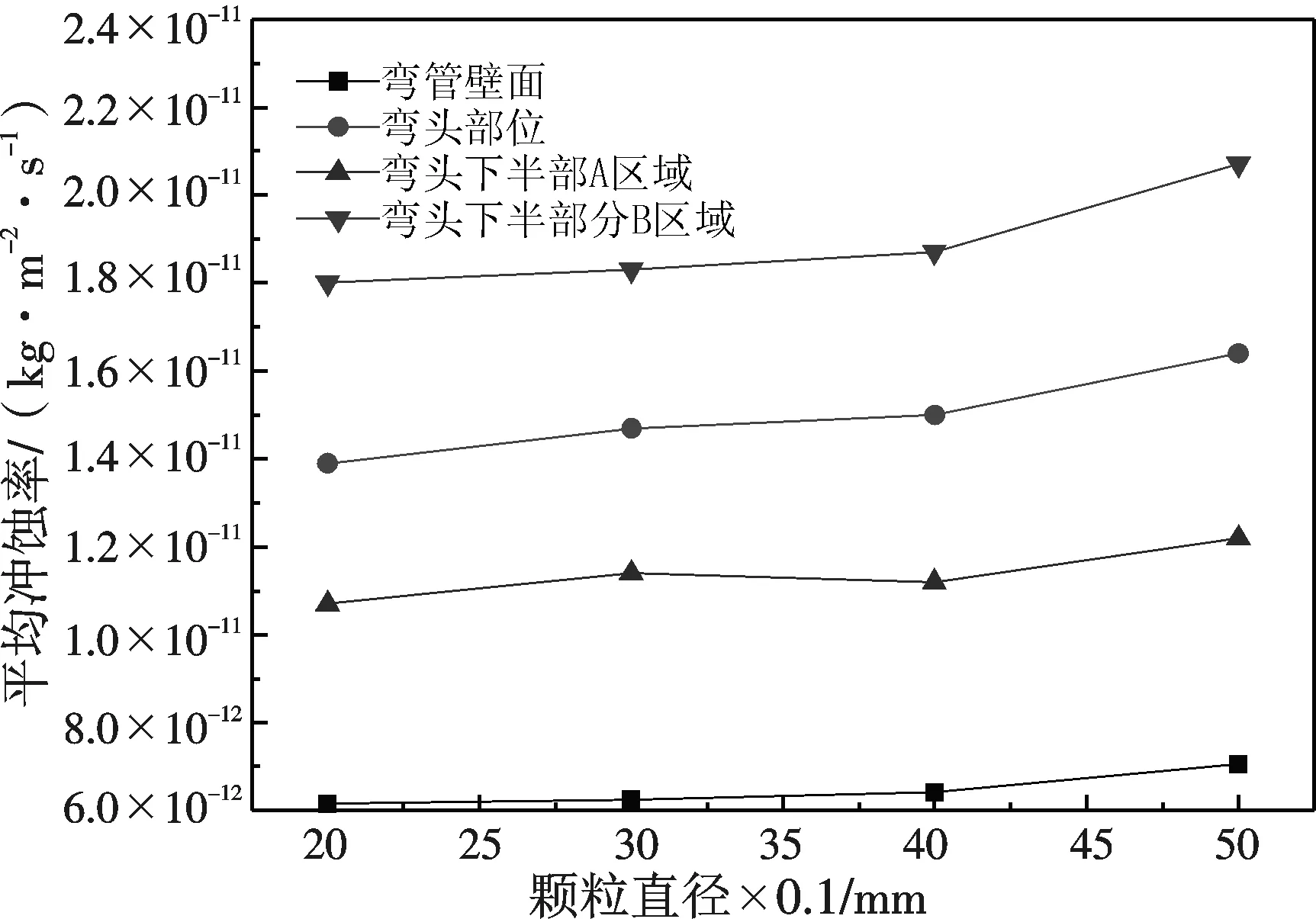
图8 相同速率、颗粒携带率比较

在保持水流入口速度、沙粒质量流量一定的情况下，含沙粒水流对弯头壁面的冲蚀情况见图7．随着沙粒直径的增大，沙粒对壁面的冲蚀作用出现了减弱的趋势．这是因为：在保持恒定质量流量1 kg/m3的情况下，沙粒直径增大，则沙粒携带量下降了，即沙粒的数量大幅度减少,导致沙粒撞击弯头壁面的总次数降低，尽管沙粒的直径增大，单个沙粒的能量增大了，但总的来说沙粒对弯头壁面的冲蚀作用减弱了．这个结果与冯进[1、8]等人的研究并不矛盾．为验证这个问题，又分别进行了4组模拟．在适当增大沙粒质量流量的情况下，即保持同样的粒子携带量，发现沙粒对弯头壁面的冲蚀率随着沙粒直径的增大而增大，如图8所示．

综合图5～8得出：不管在上述哪种情况下，弯头部位受冲蚀是最严重的，并且主要是发生在弯头的下半部分B区域．已经求解了在各种工况下弯头的冲蚀率，就容易得出弯头在一定时间间隔内的磨损量了，这为我们进行含颗粒流体输送管路的合理设计提供了依据，比如可在管路曲率变化较大的部位进行适当的加厚，也可以对局部进行强化处理等．

4 结论

(1)管道中冲蚀最严重的部位是管路曲率发生变化的部位，且冲蚀程度随弯头部位截面的转角α的增大而增大，冲蚀最严重的部位位于弯头的下半部B区域．

(2)颗粒直径一定，流体速度越大，则颗粒对弯管的冲蚀作用也越大；在速度一定且颗粒携带量相同的情况下，流体夹带的颗粒直径越大则颗粒对弯管部位的冲蚀作用也就越大，如果仅仅速度不变，颗粒携带量减少，颗粒的直径越大，则其冲蚀作用反而有下降的趋势．

(3)稀薄颗粒流体对管道的冲蚀作用尽管有限，但在长年运行时其危害也不容忽视．

参考文献：

[1] 冯 进,张慢来,冯 仲.带粒液流中圆形弯管的冲蚀模型研究[J].长江大学学报:自然科学版, 2008,5(3):74-80.

[2] 黄 勇,蒋晓东,施哲雄. 弯头的冲蚀问题及其预测和预防[J].炼油技术与工程, 2005,35(2):33-36.

[3] FAN J R, ZHANG X Y, CHEN L H. New stochastic particle dispersion modeling of a turbulent particle-laden round jet[J].Chem Eng J, 1997,66(3):207-215.

[4] 姚 军,陈丽华,樊建人.一种气固两相流中弯管抗磨方法的数值试验研究[J]. 中国电机工程学报, 2002,22(5):134-138.

[5] 郑有取,张育新. 90°方形弯管内颗粒冲蚀磨损研究[J]. 热力发电, 2007(4)：34-37.

[6] KLIAFAS Y, HOLT M. LDV measurements of a turbulent air-solid two-phase flow in 90° bend[J]. Exp in Fluids, 1987,5(2):73-85.

[7] 陈孙艺.流体对管件冲蚀的研究和防护[J]. 石油化工腐蚀与防护, 2003,20(5)：59-62.

[8] 田贵山,王新军,徐廷相.垂直管内气固两相湍流模型及其数值计算[J]. 西安交通大学学报, 1998,32(7)：41-45.

[9] TANAKA K, SUGENO M. Stability analysis and design of fuzzy control systems[J]. Fuzzy Sets and Systems, 1992,45(2):135-156.

[10] 柳成文,毛靖儒, 俞茂铮.90°弯管内稀疏气固两相流及固粒对壁面磨损量的数值研究[J].西安交通大学学报, 1999,33(9):53-57.