一种公平的动态轮转算法
2012-11-22赵碧海熊慧军
胡 赛,赵碧海,2,熊慧军
(1.长沙学院信息与计算科学系,中国 长沙 410003;2.中南大学信息科学与工程学院,中国 长沙 410083)
现代操作系统已经从原来的单任务模式演化成多任务并发模式.CPU作为一种主要的计算资源,被多个任务同时竞争使用.为任务分配CPU时,调度程序应尽量保证对所有任务公平,同时获得最小的周转时间、响应时间和上下文切换次数.时间片轮转算法作为一种最经典的调度算法得到了广泛的应用,尤其在分时操作系统中.国内外许多学者对此展开了大量的研究,并提出了一些改进的算法.为了获得更小的等待时间,文献[1~4]修改了时间片的设置方式,时间片长度由任务的服务时间决定,文献[5]修改了轮转算法在同一周期内的调度策略;为了追求更好的公平性,文献[6,7]提出以任务的到达时间和服务时间作为优先调度的依据.文献[8~9]研究了实时系统和嵌入式系统环境的轮转算法.Shukla使用马尔科夫链模型分析了FCFS服务算法、时间片轮转算法和多级队列算法发生状态转移时的概率关系[10-11],Pandey[12]教授分析了任务的服务时间与每次轮转完成的任务数量之间的关系,提出了一种两级队列的时间片轮转算法.上述这些算法只注重提高性能的某一方面而忽略了其他方面,如为了追求更好的等待时间而牺牲算法的公平性;缺乏严格的数学分析,模拟仿真不具有普遍性.本文通过综合时间片轮转算法、短作业优先算法和多级队列算法,提出一种公平的动态轮转算法.
1 算法设计
1.1 定义及相关符号说明
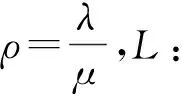
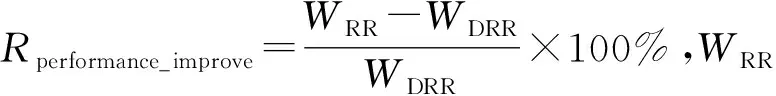
定义2若进程调度过程具有下列性质:
(1)进程到达等待队列的数量服从参数为λ的泊松分布,时间间隔服从参数为λ的指数分布;
(2)进程服务时间服从参数为μ的指数分布;
(3)在一个无限短的时间间隔内只有一个进程到达或离开.
则称之为一个生灭过程.
1.2 动态轮转算法
本文提出的动态轮转算法(DRR)综合了短作业优先算法、时间片轮转算法(RR)和多级队列调度算法.传统时间片轮转算法中每个进程获得的时间片相同.从公平的角度来说,运行时间长的进程希望得到更多的时间片,因为它们等待的时间更长.多级队列调度算法解决了这一问题,比时间片轮转算法具有更好的公平性.但是这种算法又带来了另一种不公平.由于算法采用多个队列,调度程序从当前队列中调度进程前会检查优先级高于当前队列的等待队列中是否有进程,若有进程在等待,则会优先调度优先级较高的队列中的进程,直到所有优先级较高的队列中都为空时才调度当前队列中的进程.由于有新进程不断进入,那些沦入优先级低的队列中的进程虽然得到了较长的时间片,却一直得不到被调度的机会,甚至会出现某些进程长时间在队列中休眠.
针对时间片长度的选取,动态轮转算法综合了时间片轮转算法和多级队列算法的优势.处于就绪状态的进程在等待队列中等候调度,每个进程被调度时所获得的时间片长度各不相同:进程首轮调度时,时间片长度为固定值a,从第二轮开始,进程所得到的时间片长度与该进程已经获得的CPU服务时间成正比.用Ti表示进程第i轮调度时得到的时间片长度,则
进程控制块(PCB)包含有进程的各种计时信息,进程的调度次数和已经获得的CPU的时间,进程被调度时,从PCB中获取调度次数和执行时间,并以此计算出本次调度可获得的时间片长度,调度结束后对PCB中的该部分信息进行更新.
华金先生曾指出,在允许优先占用时,对需要服务时间短的顾客给与高优先权的方式是减少平均等待时间的好办法.基于这一思想,在调度策略上,本文采取短作业优先算法和时间片轮转算法相结合,即在同一个轮转调度周期内将原有的先来先服务的调度方式改为短进程优先的方式,并在算法中引入了服务队列的概念.服务队列是指等待队列中的进程按照所需服务时间从短到长的顺序排列而形成的进程序列,进程调度程序从服务队列中调度进程并获取CPU的服务.
以下是算法的具体步骤:
算法 DRR(P,a,b)
输入:随机产生的进程集P{p1,p2,…,pn},初始时间片长度a,时间片增长系数b;
输出:平均周转时间W,平均响应时间Wr;
1.W=0;Wr=0;RemainProcess=Length(P);
2.While RemainProcess>0 do
2.1 fori=0 to Length(P)-1 do
2.2 ifP[i]是刚抵达等待队列的新进程
2.3 根据P[i]的类型及资源需求预测P[i]的服务时间
2.4P[i]进入服务队列;
2.5 NewCount = NewCount + 1;
2.6 if NewCount>0 then
2.7j=新进程在队列中的位置
2.8 if (NewCount>0) and (j 2.9 CurrentProc=P[J] 2.10 NewCount = NewCount-1; 2.11 Else CurrentProc =P[Top]; 2.12 从CurrentProc的PCB中读取调度次数SchedulTimes和运行时间RunTime; 2.13 if SchedulTimes=0 then 2.14T=a; 2.15 Else 2.16T=b*RunTime; 2.17 进程CurrentProc运行时间片T; 2.18 更新CurrentProcPCB中的计时信息 2.19 RemainProcess= RemainProcess-1; 3.fori=0 to Length(P)-1 do 3.1W=W+P[i]的周转时间; 3.2Wr=Wr+P[i]的响应时间; 4.W=W/ Length(P);Wr=Wr/ Length(P); 5.Output(W,Wr); 假定进程来源是无限的,进程到达时间与系统当前状态和以前的进程到达时间无关,服务时间与系统当前的状态及以前进程获得的时间无关. 当上述假设成立,进程到达等待队列的数量服从参数为λ的泊松分布,λ为到达率,CPU为进程提供服务的进程个数服从参数为μ的泊松分布,μ为服务率. 上述定义中,“生”指的是进程的到达,“灭”指的是进程的离开.生灭过程的瞬时状态一般很难求得,但可以求得稳定状态分布.对于平稳的生灭状态而言,从平均意义上讲,到达等于离开.图1是稳定的生灭过程的状态转移图. 根据分析可知,采用时间片轮转算法时,进程到达等待队列的数量服从参数为λ的泊松分布,时间间隔服从参数为λ的指数分布,服务时间服从参数为μ的指数分布.由于提供服务的CPU的数量为一个,在无限短的时间内,只有一个进程到达或离开.由定义7可知,满足生灭过程的性质.下面将利用生灭过程的状态转移图分析时间片轮转算法的平均等待时间和平均周转时间. 生灭过程的基本原理是,在任意状态下n达到稳态平衡的条件:产生该状态的平均速率=该状态转变成其他状态的平均速率,即到达等于离开. 根据上述基本原理,可得下列平衡方程. 状态 离去 进入 0λ0p0=μ1p1 1 (λ1+μ1)p1=λ0p0+μ2p2 ⋮ ⋮ n-1 (λn-1+μn-1)pn-1=λn-2pn-2+μnpn n(λn+μn)pn=λn-1pn-1+μn+1pn+1 随机变量X表示系统处于稳态时的进程数,采用时间片轮转算法时的平均队长LRR是X的数学期望.所以, 随机变量Xq表示系统处于稳态时排队等待的进程数,采用RR算法时平均等待的进程数Lq-RR可表示为 定理3若有n(n>0)个进程p1,p2,…,pn,服务时间相互独立且满足参数为μ的指数分布,则从中选取服务时间最短的进程优先执行,其服务时间满足参数为nμ的指数分布. 证由于进程p1,p2,…,pn的服务时间相互独立,且均满足参数为μ的指数分布,因此不妨用随机变量X1,X2,…,Xn分别表示它们的服务时间分布.则根据指数分布的定义,X1,X2,…,Xn的概率密度可分别表示为f1(x)=μe-μx,f2(x)=μe-μx,…,fn(x)=μe-μx,x>0,分布函数可分别表示为F1(x)=1-e-μx,F2(x)=1-e-μx,…,Fn(x)=1-e-μx,x>0. 若用随机变量Z表示从n个进程中取服务时间最短的进程的服务时间的分布,则有Z=min(X1,X2,…,Xn),Z的分布函数可表示为Fmin=1-(1-F1(x))(1-F2(x))…(1-Fn(x)).由于X1,X2,…,Xn相互独立且具有相同分布,所以Fmin(z)=1-(1-F1(z))n=1-(1-(1-e-μz))n=1-e-nμz(z>0).于是Z=min(X1,X2,…,Xn)的概率密度为fmin(z)=nμe-nμz(z>0),满足参数为nμ的指数分布. 本文提出的基于短作业优先的动态轮转算法(DRR)是对RR算法的服务方式的改进,进程的到达方式并未改变.因此采用DRR算法时,进程到达等待队列的数量仍然服从参数为λ的泊松分布,到达的时间间隔服从参数为λ的指数分布.关于服务方式,DRR算法不再采用原有的先来先服务方式,而是每次从服务队列中选择所需服务时间最短的一个进程调度执行.若队列中有n个进程,根据定理3,从n个进程中选择服务时间最短的进程执行,服务时间满足参数为nμ的指数分布,所以采用DRR算法时,仍满足生灭过程的定义,故本文将借助生灭过程中处于稳定状态时的状态转移图分析DRR算法的平均周转时间和平均等待时间. 当系统处于稳态时,DRR算法将从λ个进程中选取服务时间最短的进程执行.若用μ′表示DRR算法的服务率,则根据定理3,μ′=λμ. 当系统处于稳态时,采用DRR算法时的平均队长LDRR可表示为 平均等待的进程数Lq-DRR可表示为 根据分析可知, 当系统处于稳态时有,μ>λ>1,WRR-WDRR>0, (μ+λ)(μ(μ+λ)-λ)-(μ-λ)>(μ+λ)(μ(μ+λ)-λ)-(μ+λ)=(μ+λ)(μ2-1+ λ(μ-1))>0 . 由此可见,相比RR算法,采用DRR算法之后,进程的平均等待时间和平均响应时间都有所降低,这表明DRR算法的性能要优于RR算法.接下来本文将进一步分析2种算法之间的差异. 衡量调度算法的指标除了平均周转时间和平均响应时间外,系统开销也是非常重要的, DRR算法时间片动态增长,进程每次调度都能获得比上次调度更长的时间片长度,能有效地减少进程调度的次数.系统在发生进程切换时,需要保留CPU的现场信息,同时引发进程上下文的切换,增大了系统开销,因此通过时间片增长缩减调度次数的方式,能有效地降低系统开销. 综上所述,改进的动态轮转算法的综合性能优于传统的时间片轮转算法. 以下分别用improve_turn,improve_wait,improve_response,improve_switch表示平均周转时间提高比,平均等待时间提高比,平均响应时间提高和平均切换次数提高比. 本文将传统的RR算法和自适应的DRR算法分别模拟调度实现.本次实验基于Windows平台,采用Matlab程序模拟实现.模拟系统包括任务生成模块和调度模块两部分.任务生成模块负责随机生成任务,任务到达时间和估计服务时间,由系统在设定的区间内随机生成.任务数量和服务时间变化区间大小是可调大小参数,以验证任务数量和服务时间对算法性能的影响; 调度模块分别采用RR算法和DRR算法调度任务生成模块产生的任务. 本次实验应达到如下3个目的:1) 在模拟调度环境下,对比RR算法和DRR算法的综合性能差异.2) 研究不同的任务数目和服务时间跨度对2种算法性能的影响.3) 研究RR算法时间片长度对两种算法性能差异的影响. 为此,本文设置了4组实验. 实验1RR算法与DRR算法综合性能比较 本次实验生成50个任务,预期服务时间在区间[1,1 000]内随机产生,RR算法的时间片q=50,DRR算法的增长速率调节参数b=2. 实验结果如图2所示,X轴表示实验次数,Y轴表示性能提高比.从图2可以看出,平均周转时间和平均等待时间缩短了20%左右,平均响应时间缩短了98%,平均切换次数减少了17%~35%.从实验结果可知,DRR算法的综合性能优于传统的RR算法. 图1 状态转移图 图2 RR算法与DRR算法的综合性能比较 实验2任务数目对算法性能的影响 本次实验任务数目设定在区间[2,1 000]内,任务到达时间随机产生,预期服务时间在区间[1,2 000]内随机产生,RR算法的时间片q=50,DRR算法的增长速率调节参数b=2. 实验结果如图3所示,其中X轴表示任务数目,Y轴表示性能提高比.由图3可以看出,平均周转时间缩短了10%~30%,平均等待时间缩短了19%~30%.随着任务数目的增加,平均周转时间提高比和平均等待时间提高比缓慢提高,平均切换次数减少了50%~70%,随着任务数目的增多,平均切换次数提高比有所降低.由此可见,任务数目越多,DRR算法的综合性能优势逐步增大. 实验3服务时间跨度对算法性能的影响 本次实验生成50个任务,任务到达时间随机产生,任务预期服务时间跨度为1 000~25 000,RR算法的时间片q=50,DRR算法的增长速率调节参数b=2. 实验结果如图4所示,其中X轴表示任务预期服务时间,Y轴表示性能提高比.由图4可以看出,随着预期服务时间跨度增大,平均切换次数提高比不断增长,而平均周转时间和平均等待时间提高比呈波浪式缓慢增长.当服务时间跨度在b(1+b)i(i>0) ms左右时,性能提高比位于波峰;而当服务时间跨度在b(1+b)i~b(1+b)i+1ms之间,性能提高比位于波谷.由此可见,任务服务时间跨度增大,DRR算法的综合性能优势缓慢增长. 综上所述,在模拟调度环境中,DRR算法的综合性能优于RR算法.当任务数目增多,服务时间跨度增大时,DRR算法的性能更优, RR算法的时间片较小时,DRR算法的平均切换次数更优, RR算法的时间片增大时,DRR算法的平均响应时间优势增大. 图3 任务数目对算法性能的影响 图4 任务服务时间跨度对算法性能的影响 本文提出一种改进的动态轮转算法,算法将同一轮转周期内先来先服务方式改进为短作业优先方式,有效地缩短了进程的平均周转时间;将时间片由原来的定长方式修改为根据累计运行时间而自适应地动态增长方式,解决了原有的轮转方式中存在的时间片长度选取的矛盾,同时也提高了进程的响应时间,缩短了平均周转时间和等待时间. 本文的分析是以进程服务时间服从指数分布为前提.下一步工作中,我们将分析服务时间服从一般分布时算法如何有效工作等问题. 参考文献: [1] BEHEAR H S, MOHANTY R, DEBASHREE N. A new proposed dynamic quantum with re-adjusted round robin scheduling algorithm and its performance analysis[J].Inter J Comput Appl, 2010,5(5):10-15. [2] RAMI J M. Self-adjustment time quantum in round robin algorithm depending on burst time of the now running processes[J].Am J Appl Sci, 2009,6(10):1831-1837. [3] SAAD Z R, SAFWAT H H, SAMIH M. Improving waiting time of tasks scheduled under preemptive round robin using changeable time quantum[EB/OL]. 2010, http://arxiv.org/abs/1003.5342. [4] RAKESH K Y, AHHISHEK K M, NAVIN P. An improved round robin scheduling algorithm for CPU scheduling [J].Inter J Comput Sci Eng, 2010,2(4):1064-1066. [5] MAMUNUR R, NASIM A. A new multilevel CPU scheduling algorithm [J].J Appl Sci, 2006,6(9):2036-2039. [6] HELMY T, DEKDOUK A. Burst round robin as a proportional-share scheduling algorithm[C]//IEEE-GCC, Urumchi, Xinjiang, China, 16-18 Aug, 2007. Wiley:IEEE Computer Society Press, 2007:424-428. [7] MOHAMMED A. Best-job-first CPU scheduling algorithm [J].Infor Tech J, 2007,6(2):288-293. [8] YAASHUWANTH C. A new scheduling algorithms for real time tasks [J].Inter J Comput Sci Infor Security, 2009,6(2):61-66. [9] PANDURANGA R M, SHET K,ROOPA K. A simplified study of scheduler for real time and embedded system domain[J].Inter J Comput Cog, 2009,5(22):60-73. [10] SHUKLA D, OJHA S, JAIN S. Data model approach and Markov chain based analysis of multi-level queue scheduling [J].J Appl Comput Sci Math, 2010,8(4):50-56. [11] SHUKLA D, JAIN S, SINGHAI R,etal. A Markov chain model for the analysis of round-robin scheduling scheme[J].J Adv Network Appl, 2009,1(1):1-7. [12] PANDEY D, VANDANA. Improved round robin policy a mathematical approach [J].Inter J Comput Sci Eng, 2010,2(4):948-954.2 算法分析
2.1 时间片轮转算法分析
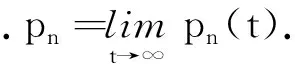
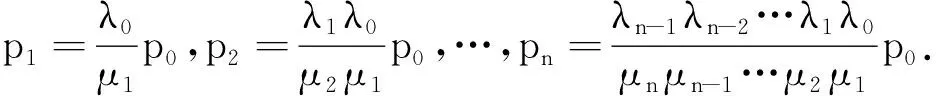
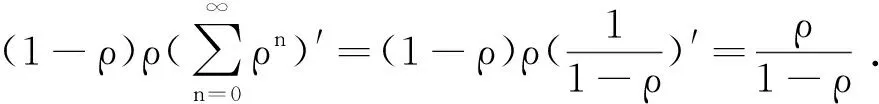
2.2 改进的动态轮转算法分析
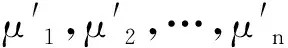
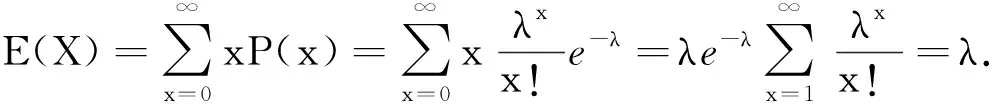
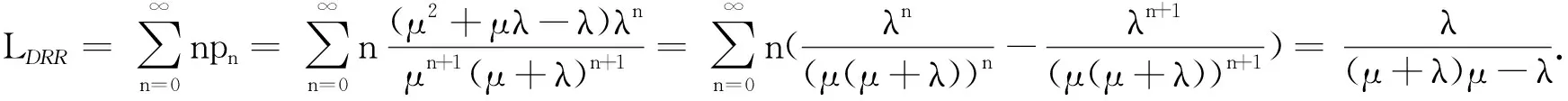
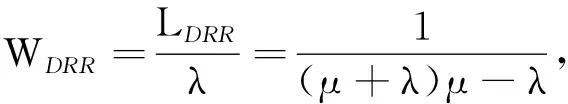
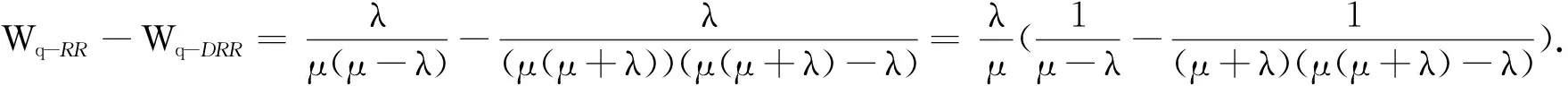
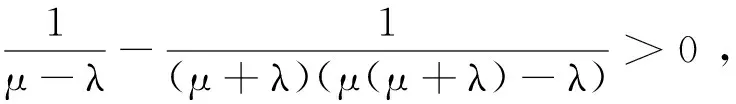
3 模拟实验和结果分析

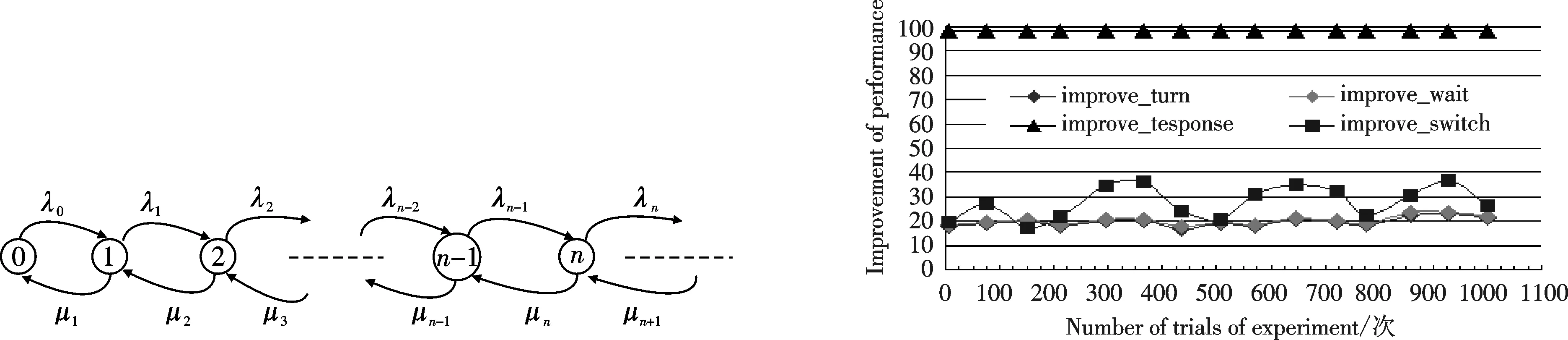
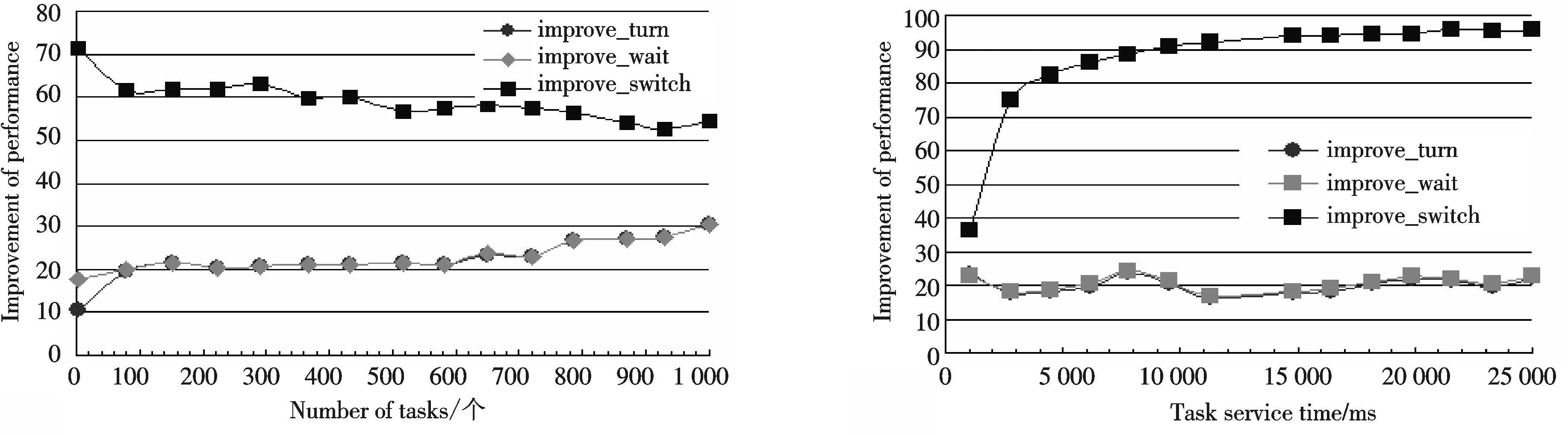
4 结论及进一步研究工作
