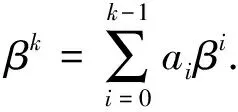可逆可对角化矩阵最小多项式的行列式表示法
2012-11-22龚和林舒情
龚和林,舒情
(上饶师范学院数学与计算机科学学院,江西 上饶 334001)
0 引言
最小多项式在向量空间的分解,矩阵的对角化,矩阵方程,微分方程组等方面均有一定的应用[2-4], 它的计算常常是对A∈n×n的特征多项式fA(λ)作标准分解,找到A的全部不同特征值λ1,λ2,…,λs,再对fA(λ)的标准分解中含有的因式按次数从低到高的顺序进行检测, 第一个零化A的多项式就是最小多项式; 此外,还有利用A的最后一个不变因子或Jordan标准形的求解方法. 这些方法往往要作标准分解, 对实际求解的过程而言这决非易事. 最近,杨继明[5]利用向量的最小多项式得到了矩阵的最小多项式一种求法:先选定一组基,用初等变换求得每一个基向量关于A的最小多项式,再确定这些向量最小多项式的公倍式(即矩阵的最小多项式).郑大彬等[6]证明了对有限维向量空间n存在某个向量关于A的最小多项式等于A的最小多项式.这表明,文献[5]中计算矩阵的最小多项式的方法是有效的.与常规方法相比,文献[5]中方法虽避开了标准分解和Jordan标准形,且便于计算机实现,但这种方法计算量随矩阵规模扩大而迅速增加.因此存在一定的局限性. 本文中目的就是改进上述的初等变换法,充分利用线性空间的同构概念及初等变换特点,提出一种新的求矩阵最小多项式初等变换法. 特别地, 对可逆可对角化矩阵, 用行列式建立其最小多项式的显式公式.
1 相关概念及基本引理
首先我们回顾线性代数的一些基本知识(参见文献[7]).
引理1.1[7](Cauchy-Binet公式)设A∈m×n,B∈n×m,则
这里,求和遍历A和B的最大m阶主子式.
引理1.2[7](Cayley-Hamilton定理)设A∈n×n,则fA(A)=0.

令A∈n×n,k∈0,λ1,λ2,…,λn是A的全部特征值(重根重复计算). 定义且
注意:A0=I,μk=trAk.显然,|V|=∏1≤i 引理1.4设A∈m×n,k∈+,Δk为Δ的第k阶顺序主子式,且A存在k个不同非零特征值, 则 引理1.5设映射σ:n×n→n2,且∀则σ是n×n到n2上的同构映射. 引理1.5的证明易知σ是双射,又∀a,b∈,A1,A2∈n×n, 有 即σ保持加法与数量乘法运算, 故σ是同构映射. 文献[8]中证明了A∈n×n有k个不同特征值的充分必要条件为Δ的k阶顺序主子式Δk≠0,而阶数大于k的顺序主子式Δk+1=…=Δn=0.在其方法基础上,得出一个改进的结论是: 引理1.6对矩阵A∈n×n,A恰有k(k∈+)不同特征值的当且仅当Δk>0,但Δk+1=0. 引理1.6的证明众所周知,矩阵为半正定矩阵的一个充分必要条件是它的一切主子式非负.当然,Δ=VVT(半正定)一切顺序主子式非负. 显然,必要性由文献[8]中的结论蕴涵. 反过来,令N为A的不同特征值数目,一方面,Δk>0,则 定理2.1设A∈n×n,k∈+,且n2×(n+1),M可经适当行初等变换化为且 定理2.1的证明在线性空间n×n中,令k是满足Ak是I,A,…,Ak-1的线性组合的最小的正整数. 由引理1.2知,这样的“k”是存在的,且k≤n. 不妨设则事实上,令则deg(mA(λ))=k,否则,存在s∈+,s 定理2.2设A∈n×n是可逆的可对角化矩阵,Δk是Δ的第k阶顺序主子式,Δk+1[1,x]为Δk+1的第1行第x列元素的代数余子式. 若Δk>0, 且Δk+1=0, 则 (1) μ0x1+μ1x2+…+μk-1xk=μk (2) 也即向量等式(1)式的解X=(m0,m1,…,mk-1)也是下列方程组的解 (3) [1] 蓝以中.高等代数简明教程(下册)[M].北京:北京大学出版社,2002. [2] 胡瑞平.矩阵方程AX-XB=C的最小多项式解法[J].应用数学学报,1993,16(3):295-301. [3] 王子瑜,陈华如.矩阵最小多项式在微分方程组中的应用[J].铜陵学院学报,2004(3):69-70. [4] 黄可滃.用最小多项式求线性微分方程组的基解矩阵[J].绍兴文理学院学报,2006,26(7):31-33. [5] 杨继明,曹军.求矩阵最小多项式的初等变换方法[J].数学的实践与认识,2004,34(10):174-176. [6] 郑大彬,刘合国.关于向量的最小多项式[J].湖北大学学报:自然科学版,2010,32(4):349-356. [7] Horn R A, Johnson C R. Matrix analysis[M].Cambridge:Cambridge University Press,1985. [8] 梅宏.n次代数多项式有m个不同根的充要条件[J].数学的实践与认识,2002,32(2):335-337.

2 主要结论及其证明