车用电机定子振动特性的影响因素分析及优化

张范辉，左曙光，何吕昌，陈瑞峰

(同济大学，上海201804)

0 引 言

电磁噪声是永磁电机噪声的主要组成部分，电磁径向力作用产生的定子振动变形是电机电磁噪声的主要根源。通过试验与仿真相结合的模态分析方法，对电机结构的模态参数进行识别、分析、评价，并找出电机结构动态性能上存在的问题，然后根据电机结构固有模态的分析结果预测并控制电机噪声［1］。

国内外众多学者在电机结构固有模态方面开展了广泛的研究，取得了较多研究成果。文献［2］将有限元模态分析应用到感应电机和超声波电动机定子振动分析上，取得了较好的效果。文献［3］研究了铁心厚度和铁心长度对电机结构固有模态的影响。文献［4］分析了机壳、散热片及出线箱对开关磁阻电机定子固有模态的影响，研究表明铁心和机壳的厚度对固有频率影响较大;铁心和机壳的长度对定子的平面振型影响较小;散热片和出线箱降低了定子结构低阶固有频率，提高了高阶固有频率。文献［5］对开关磁阻电机定子结构的固有模态进行了分析，对不同绕组工艺和散热筋结构条件下的固有频率进行分析和比较。

但是现有的文献没有对电机定子总成的齿数、轭厚、定子轴向长度、铁心外径和机壳厚度等结构参数的各阶固有频率的影响灵敏度进行分析和优化。

本文以某电动小车驱动用永磁电机为研究对象，基于低噪声、高声品质驱动电机的设计要求，采用三维有限元法，对电机定子结构实现参数化建模，并对各参数对电机定子固有频率的灵敏度进行分析。以此为依据对定子进行了优化设计，为低噪声、高声品质的电机结构设计和结构优化提供参考。

1 定子有限元建模及试验验证

1.1 电机定子有限元建模

电动汽车用无刷直流驱动电机定子的实际结构如图1 所示。它包括定子机壳、定子铁心和绕组，其中铁心和机壳采用过盈配合紧密贴合在一起，绕组以一定的方式缠绕在定子铁心上。

图1 直流无刷驱动电机定子总成结构

在ANSYS 中对该电机定子总成进行建模，其中铁心材料为硅钢片，机壳材料为铝合金，绕组材料为铜。各组件的材料参数如表1 所示。

对于定子有限元建模，由于铁心和机壳属于紧密连接，所以采用共节点的方式处理。但是定子绕组的处理方式一直是一个难点，目前还没有统一有效的建模方法，只能通过绕组的特征来建立对应的有限元模型。

本文通过6 种绕组处理方式，建立有限元模型:忽略绕组质量、绕组质量归入内部绕组、绕组质量归入端部绕组、绕组质量归入铁心、绕组质量归入铁心齿、考虑全部绕组质量［6］。最后通过与模态试验结果进行分析比较，选出了与实际相符的等效模型。将绕组质量归入端部绕组的模型，即只考虑端部绕组，将其与定子铁心直接相连接，内部绕组的质量均匀归入端部绕组中，而端部绕组密度通过换算而得。利用ANSYS 的APDL 语言，采用全参数驱动的方法，建立电机定子参数化有限元模型，包括铁心、绕组、机壳以及端盖和接线盒等结构。定子的有限元模型如图2 所示。

图2 定子有限元模型

当前定子振动特性的研究只是分析了定子结构参数对定子铁心的振动特性的影响，而经研究发现，定子端盖的加入使得定子整体的模态频率有了很大的变化，因此，考虑定子结构参数影响时应该要将端盖加入，这样才与实际更加相符。

1.2 电机声振测试试验

为获得电机的实际振动特性，在电机NVH 测试台架上进行了电机声振测试，如图3 所示。试验台架由电机、联轴器和电涡流制动器构成，电涡流制动器的噪声很小，不会影响电机的振动噪声特性。

图3 电机振动噪声试验

有限元模型得到的前8 阶模态频率与试验结果对比如表2 所示，振型均相同，且振型的次序也一样，仿真结果与试验结果有很好的一致性。说明本文所建的有限元模型是准确的，可用于进一步的电机定子振动噪声特性分析。

表2 有限元模型与试验所得模态频率对比

1.3 振动能量分布对比分析

在定子内部施加仿真所得的电磁激振力，在机壳外表面一点拾取响应。将稳定工况下得到的机壳外某点的振动信号与仿真模型机壳外同一点的振动信号在整个频段上的能量分布进行统计分析并比较，得到的结果如图4 所示。

图4 实测振动信号与仿真信号能量分布

从图4 中可以看出，振动信号分布在0～5 000 Hz 的宽频范围内，尤其在0～2 000 Hz 内能量很高，且随振动频率的增加，幅值比例呈现降低的趋势。实测振动信号和仿真模型所得响应在整个频域上的能量分布情况大致相同，这进一步表明有限元模型的正确性。

对比表2 和图4 可得，电机定子的前8 阶模态频率分布在4 000 Hz 以下，可能引起与电磁径向力波的共振，导致电机振动和噪声的增大。因此，需要对现有电机定子的结构进行优化，使得定子的固有频率尽可能避开电磁力波的频带。

2 定子结构参数灵敏度分析

为了对电机定子进行优化设计，首先需要确定对定子振动特性影响较大的结构参数，故需要进行电机定子结构的参数灵敏度分析。由于电机电磁噪声的主要频率分布在700～5 000 Hz 范围内，因此我们选取前10 阶模态进行研究。

在参数化模型中，通过直接求导法求出定子在实际尺寸处的模态频率对各参数的变化率，观察定子模态频率随参数变化的情况，结果如表3 所示。其中齿数对应的灵敏度单位为Hz/齿，其他参数对应的灵敏度单位为Hz/mm。

表3 结构参数对各阶模态频率的灵敏度

从表3 中可以看出各参数对各阶模态影响的灵敏度。对于端面为椭圆的振型，机壳厚度对其影响最大，其次是轭厚;对于端盖的局部模态，由于约束一般都是加在端盖上，加约束之后此阶模态刚度会大幅增加，因此不对其作分析;对端面形状为椭圆两端面反对称的振型，机壳厚度和铁心外径对其影响最大，轭厚次之，齿数和轴向长度对其影响较小;对于端面为三角形的振型，轭厚对其影响最大，其次是铁心外径和机壳厚度，齿数和轴向长度的影响很小;对于两端面做剪切运动的振型，机壳厚度和铁心外径对其影响最大，其中机壳厚度为正向影响，铁心外径为负向影响，其他三个参数影响均较小。

3 定子结构优化设计

根据灵敏度分析结果，本文在10 kW 电动汽车驱动用无刷直流电机现有结构基础上，通过改变参数(主要针对机壳厚度和铁心外径)，对定子结构进行优化。

表4 实际电机的参数

在电机的设计中，定子内径Di1和铁心有效长度

lef是两个主要尺寸，由电机的性能参数来确定［7］。主要尺寸与电机的功率、电磁负荷及转速等参量之间的关系式:

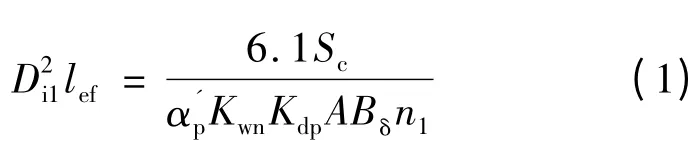
式中:Sc为计算视在功率;α′p为计算极弧系数;Kwn为磁场波形系数;Kdp为定子绕组系数;n1为额定转速;Di1为定子内径;lef为铁心有效长度;A 为线负荷;Bδ为气隙磁通密度幅值。

定子有效长度lef与极距之比称为主要尺寸比λ，中小型电机主要尺寸比取值范围如表5 所示。

表5 中小型电机主要尺寸比值范围

为保证电机原有性能不变，式(1)的右边应该保持不变，即D2i1lef= 16 224 200 mm 为定值(根据厂家提供参数计算)。极数为6，由表4 可知，λ 应在1. 42～2．32 范围内，在此选取1．42～1．6;极距τ =68 mm，由确定lef的范围为96～109 mm;铁心内径由确定为122～130 mm;最后根据铁心内外径之比确定出铁心外径为162～200 mm;由于现有机壳厚度为4 mm，已经足够小，考虑到结构强度要求，选4～8 mm。另外定子轭厚也不可以过小，设定最小值为5 mm。

优化的目的主要是让定子的固有模态频率处于径向电磁力波的频率范围之外，以防止产生共振。通过分析得到额定工况下径向电磁力波频谱图如图5 所示。

图5 径向电磁力波－时间频谱

径向电磁力波的能量主要集中在前三阶，其频率均小于2 000 Hz，而定子的一阶固有模态频率为2 113 Hz，所以可以通过提高fs1的值来降低电机的电磁噪声。将优化目标函数设定为。优化时要保证尽量小的电机体积，这里设定约束条件为优化后电机的周向外轮廓尺寸不大于原电机尺寸。

在ANSYS 中编写优化程序，采用零阶优化算法进行优化，共进行了22 组分析，目标函数值最小的一组为最优解，对应的电机参数如表6 所示。

表6 优化前后电机总成参数对比

将优化后的参数重新建立电机定子模型，并分析模态频率，然后与优化前的模态频率进行对比，结果如表7 所示。

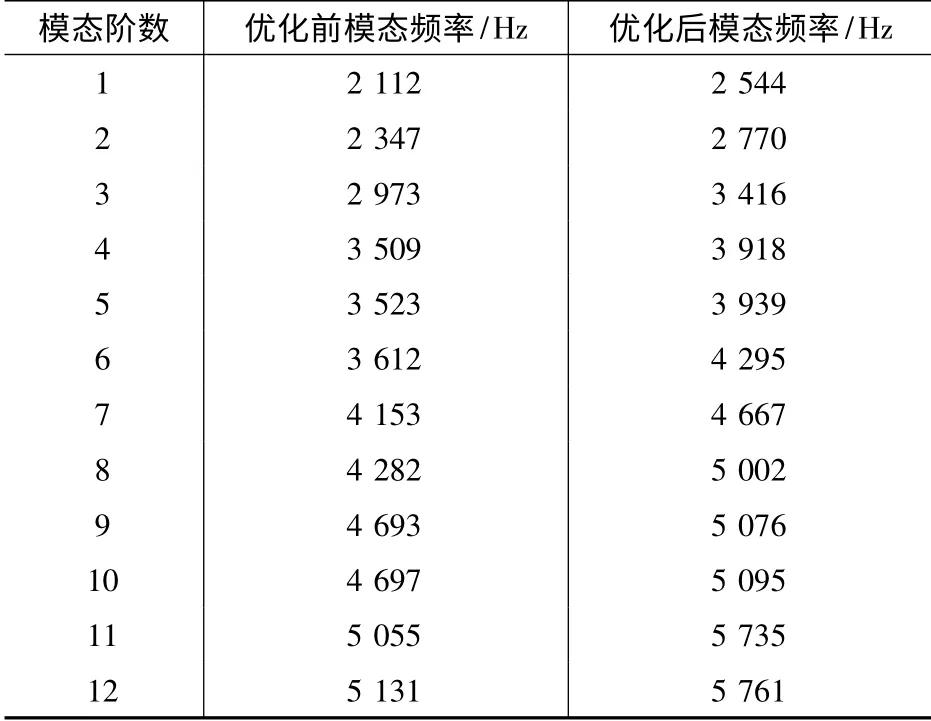
表7 优化前后定子模态频率对比

由表7 可以看出，优化后定子总成的模态频率有了较大的提高，其中第1、2 阶模态频率的增幅超过了400 Hz。而5 000 Hz 以下的模态阶数由10 阶减少到了7 阶，既减小了定子总成模态频率频带与电磁噪声常发频带的交集范围，又降低了电磁噪声频带范围内的模态密度，从而改善了电机的振动噪声特性。

按照电机在车上的安装情况，将两端盖进行全约束，分别在优化前后的定子内部施加仿真所得的电磁激振力，从机壳外表面同一位置拾取响应，得到优化前后定子总成响应对比情况，如图6 所示。

图6 优化前后定子总成响应对比

从图6 中可以看出，两端盖约束后，定子总成固有频率进一步上升，优化前第一阶模态频率在2 500 Hz 左右，而优化后增加到2 800 Hz 左右;在整个频域上，优化后响应的幅值比优化前有所降低。

4 结 语

本文根据模态试验建立了定子的参数化有限元模型，并通过电机振动噪声试验，验证了模型的正确性。对影响电机声振特性的结构参数进行了灵敏度分析，并以分析结果为依据，利用ANSYS 软件对定子结构进行了优化设计，改善了电机的振动噪声特性。得到的结论如下:

(1)建立定子有限元模型时，将绕组质量归入端部绕组的等效模型与实际最为接近。

(2)铁心外径和机壳厚度对定子总成固有频率的影响最大，轭厚、齿数及轴向长度影响较小。

(3)通过确定铁心长度、外径及其半径差，机壳外径及厚度的最优值进行结构优化，定子总成各阶模态频率均有较大的提高，避开了与径向电磁力波共振的频率范围。定子总成对电磁力波激励的响应幅值在整个频域上都有所下降。

(4)在不改变电机性能的情况下，优化后定子总成的总体积减小，且质量减小，有利于整车轻量化。

［1］ Hall K，Mueller T．Coupled vibration isolation suppression system for space applications:aspects of structural design［J］．Smart Structures and Integrated Systems，1995:136－144．

［2］ 莫岳平，胡敏强，徐志科，等．超声波电机振动模态有限元分析［J］．中国电机工程学报，2002，22(11):92．96．

［3］ Verma S P．Noise and vibrations of electrical machines and drives:their production and means of reduction［C］/ /Proc IEEE Int Conf Power Electron Drives Energy Syst Ind Gro．New Delhi，1996:1031－1037．

［4］ Cai W，Pillay P，Tang Zhangjun．Impact of stator windings and end－bells on resonant frequencies and mode shapes of switched reluctance motors［J］．IEEE Transactions on Industry Applications，2002，38(4):1027－1036．

［5］ 孙剑波，詹琼华，黄进．开关磁阻电机的定子振动模态分析［J］．中国电机工程学报，2005(22):148～152．

［6］ Chen Ruifeng，Zuo Shuguang，He Rong，et al．Stator FEM modeling of permanent magnet synchronous motor for electric vehicle driving based on structural vibration Analysis［C］/ /The 2nd International Conference on Information Science and Engineering．2010，7:5407－5411．

［7］ 黄国治，傅丰礼．Y2 系列三相异步电动机技术手册［M］．北京:机械工业出版社，2004．