V 形直线超声波电动机运动分析和实验
2012-11-22李志荣
许 海,李志荣
(苏州市职业大学机电工程系,江苏苏州215104)
0 引 言
直线超声波电动机具有断电自锁和无电磁干扰,结构设计灵活等优点。目前,国内相关机构设计出了多种结构形式的直线超声波电动机,这些直线超声波电动机性能指标随其结构形式的不同而有较大差异。1999年,由日本学者Kurosawa 提出了一种由两个兰杰文振子组合成“V”字形的大推力、高速压电振子[1-2]。该结构形式充分利用了压电陶瓷的d33效应,使该型电机具有大的推力和良好的输出效率。国内一些单位试制了这种直线超声波电动机,并进行了相关的理论分析和实验测试。就目前文献而言,对这种类型电机的驱动机理已形成了共识,即该型电机振型是利用定子体的对称和反对称模态[3-4],但由于在分析上的简化,使得仍存在一些问题值得商榷。本文作者试制了该型样机,并对电机的驱动机理和驱动足的椭圆运动进行了分析,通过理论分析和模态试验得出在电机实际工作时驱动足所形成的椭圆运动为一斜椭圆,该斜椭圆的安装角θ 角对电机的机械特性有着重要影响。
1 电机结构
电机结构如图1 所示。V 形直线超声波电动机由定子和动子两部分组成,定子部分是由两个结构上完全对称且空间上相互垂直振动的兰杰文振子构成,动子即是普通直线导轨。定子的每个兰杰文振子分别由前、后金属弹性体和压电元件组成,并通过螺栓夹紧。在兰杰文振子的一阶纵振节线处用支撑板将其连接在一起,以便于整个定子体的安装固定。每个兰杰文振子的压电单元均采用4 片沿轴向极化的圆环形压电陶瓷片和电极组成。图2 是实际制作的电机定子照片。


2 电机实际工作振型的激发
对于V 形电机,驱动足处的椭圆运动由同频的对称模态和反对称模态叠加而成,对称模态与反对称模态均由两个兰杰文振子相互协调的纵向振动组成[4],如图3 所示。理论上,如果不考虑由于定子体响应电压激励时的相位差,并且假设左右压电振子完全对称,则当电机左、右兰杰文振子同时施加相同的正弦信号时,即所施加的两个正弦信号相位差为0°。左右两个兰杰文振子作同步的纵向振动,定子产生对称模态,这个对称模态在定子驱动端面上形成竖直方向的振动。当电机左、右兰杰文振子施加反向相位差180°的正弦信号时,即所施加的两个正弦信号相位差为180°,两个兰杰文振子作反相的纵向振动,定子产生反对称模态振动,这个反对称模态振动在定子驱动端面上形成水平方向的直线运动。

图3 定子的振型
然而在实际工作中,给V 型直线超声波电动机的左右兰杰文振子所施加的分别是sin(ωt)和cos(ωt)的电压信号,即所施加的两个正弦信号相位差为90°。图4 为所施加电压信号一个周期内的波动情况。这两路信号在时间上只相差,与理论分析时所加载的信号不一致,不满足上述理论上的对对称、反对称模态的激励要求。可以看出,标准的对称模态只出现在和处,同时该处的电压幅值并非所施加的正弦电压最大值。对比图4,电机在实际工作过程中,模态的激励过程并不是简单地由对称模态和反对称模态相互转移,也不存在某个只有纯粹的对称模态和反对称模态的时间段。从上述分析中可以看出,理论上的对称模态只产生在和两个时间点处。并且驱动足在竖直方向上的最高、最低位置也不是该对称模态中的最高、最低位置。实际工作状态下由对称模态所产生的最大纵向位移量仅为理论上对称模态所产生的最大纵向位移量的0.707 倍,电机实际工作时反对称模态所产生的横向位移量仅为理论上反对称模态所产生的最大横向位移量的0.5 倍。

图4 电压信号的时序图
3 驱动足的椭圆运动轨迹
通过合理的结构设计,在某一确定频率两相相位相差90°的交变电场的作用下,定子的对称模态和反对称模态可以被同时激发出来。为便于分析,首先讨论最简单的情况,如按照图5 放置电机定子。则两个兰杰文振子的一阶纵振动幅值即为定子驱动头的纵向振动幅值(X 向)和水平振动幅值(Y 向)。如果这两个兰杰文振子的纵向振幅一致,理论上驱动足的运动轨迹为圆[3]。由于实际制作的两个兰杰文振子的不可能完全一致,所以此处设两个兰杰文振子的纵振振幅,设振幅分别为A、B,则两个兰杰文振子的纵振振型函数为:

图5 驱动足安装最简情况

式中:l 为兰杰文振子的长度。
给压电陶瓷Z1 施加的电压信号:

压电陶瓷Z2 施加的电压信号:

如不考虑由于定子体响应电压激励时的相位差,则驱动足的位移随时间t 的函数:


图6 最简安装情况驱动足椭圆轨迹
Y 轴上的最高点位移为:B,在该椭圆轨迹中驱动足(接触点)的水平速度:

在X 轴方向,驱动足最大速度为Vmax= Aω。
而电机在正常装配时驱动足和滑条的位置关系如图7 所示。和图5 相比较,可以发现椭圆此时围绕原点发生了θ 角的偏转。利用直角坐标系的旋转公式:
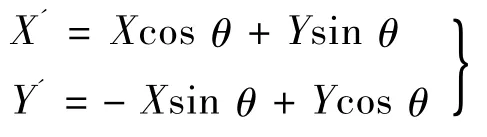
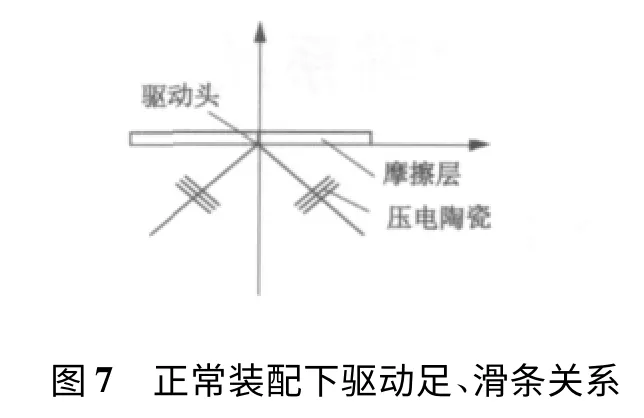
可以列写偏转后的椭圆方程:
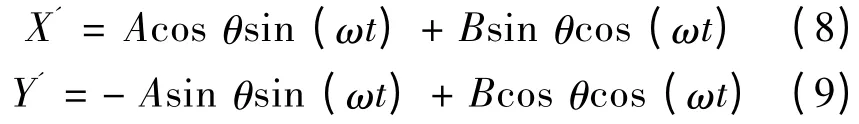
如图8 所示,在V 型电机工作时驱动足的椭圆运动并不是一个理想的正椭圆,而是一个偏转了θ角度的斜椭圆。这个斜椭圆是驱动滑条进行直线运动的驱动椭圆(理想情况下,θ = 45°)。此时驱动足的水平速度:



同理可得,在Y'方向上驱动足的最大位移:

比较图6 和图8,可以看出,实际装配关系下,驱动足的轨迹发生了θ 角的倾斜,由此造成了驱动足的最大竖直方向上的位移值和水平方向上的最大速度都发生了变化。
4 电机实验
根据有限元设计所得尺寸设计电机定子并制作样机。兰杰文振子的直径和长度分别是20 mm、58 mm,定子的质量为290 g。首先采用了PSV300F-B型高频扫描激光测振仪进行扫频实验。图9、图10分别为单独激励定子中的一个兰杰文振子的扫频曲线。从扫频曲线可看出,两者并不是严格对称的,图9 中兰杰文振子纵振频率为24.57 kHz,图10 中兰杰文振子纵振频率为26.27 kHz,两者的一阶纵振频率相差了1.7 kHz。一般超声波电动机的频率一致性应保证在1 kHz 以下,在实际驱动实验中虽然两个兰杰文振子的激振频率之间相差较大,却仍可驱动运行。在电机驱动实验中,Vpp= 300 V,f = 25 kHz,预紧力为50 N 时,接触面采用钢-钢摩擦副。电机空载最大速度为100.5 mm/s,电机最大输出力38 N。


5 结 语
本文针对V 型直线超声波电动机的定子驱动足的运动轨迹进行了分析。结合所施加信号的时序,可知实际工作中由工作电压激励,电机定子的对称模态所产生的最大纵向位移量仅为理论上的最大纵向位移量的0.707 倍。实际工作时反对称模态所产生的横向位移量仅为理论上的最大横向位移量的0.5 倍。
实际工作中,由于无法做到两个兰杰文振子的完全对称,且驱动足与滑条之间存在安装角θ,所以驱动足所形成的椭圆轨迹是一个围绕原点旋转了θ角的斜椭圆。该斜椭圆的轨迹不仅与两个兰杰文振子的纵向振幅有关,还和θ 角有关。通过理论分析可知,安装角θ 可以影响到电机的最大速度和电机最大输出推力。该角度在设计和安装时应给予精度保证。
[1] Wakai T,Kurosawa M K,Higuchi T.Transducer for an ultrasonic linear motor with flexible driving part[J].IEEE Ultrasonic Symposium,1998:683-686.
[2] Kurosawa M K,Osamu K,Yuki T,et a1.Transducer for high speed and large thrust ultrasonic linear motor using two sandwich-type vibrators[J].IEEE Transactions on Ultrasonic,Ferroelectrics,and Frequency Control,1998,5(45):1188-1195.
[3] 时运来,李玉宝,赵淳生.V 形大推力直线型超声电机的运动机理分析[J].压电与声光,2008,30(6):772-775.
[4] 杨东,姚志远.双变幅杆V 形直线超声波电动机研究[J].压电与声光,2009,31(5):685-687.
