纸浆洗涤过程中稀释因子的优化

2012-11-22单文娟

中国造纸 2012年2期

关键词：纸浆用水费用

单文娟汤伟，2

(1.陕西科技大学造纸工程学院;陕西西安，710021;2.陕西西微测控工程有限公司，陕西咸阳，710081)

纸浆洗涤过程中稀释因子的优化

单文娟1汤伟1，2

(1.陕西科技大学造纸工程学院;陕西西安，710021;2.陕西西微测控工程有限公司，陕西咸阳，710081)

基于浆料洗涤系统的整体工程思想，对洗浆系统和蒸发系统进行了物料衡算，建立了纸浆洗涤用水和稀释因子的最优化模型，并通过罚函数，将约束问题转化为无约束问题，对模型进行了寻优控制。实践表明，该方法可以找到最优稀释因子，减少了费用，降低了生产成本。

纸浆洗涤用水;稀释因子;罚函数;最优化

纸浆洗涤的主要目的是将纸浆中的可溶无机物和有机物洗净，同时获得高浓度的黑液。提取的黑液经过蒸发浓缩到一定的浓度，送入燃烧炉燃烧。水的用量和浆的处理能力是纸浆洗涤过程中的重要指标，增加纸浆洗涤系统的用水量，即增加稀释因子，可以提高纸浆的洁净程度，但会使黑液浓度降低，使蒸发系统的蒸发负荷增加，蒸汽消耗量增加。所以稀释因子的选择，不能孤立地仅从洗浆系统来考虑，必须与蒸发系统综合起来考虑，选择最优的稀释因子，使纸浆洗涤用水费用最低。

纸浆洗涤过程是一种非线性、时变和大时滞的复杂系统，本课题基于多段逆流洗涤方式及系统工程的思想，通过对纸浆洗涤系统和蒸发系统进行物料衡算［1］，建立了纸浆洗涤用水和稀释因子的最优化模型。该模型是含有稀释因子约束的非线性规划问题，本课题通过罚函数，将约束问题转化为无约束问题，对纸浆洗涤用水进行优化控制。

1 优化控制系统结构

纸浆洗涤过程中，各真空洗浆机是串联运行的，因此采用分级分组的策略，将整个系统分解成若干(如4个)相对独立的小单元，通过基本控制级实现对各个小单元的稳定控制，通过联动级将各个小单元联系起来，以适应产量及工艺参数的变化，增强系统的柔性。各浆纸企业已采用集散控制系统 (DCS)实时控制［2］，要实现稳态优化控制，可在此基础上增加一优化级，构成稳态递阶控制结构，如图1所示。

优化控制器由计算机构成，它从DCS中获得现场数据，通过优化计算向DCS传送最佳输入设定值，使系统在最优状态下运行。

图1 稳态递阶控制图

2 纸浆洗涤用水相关系统模型的建立

2.1 洗浆系统数学模型

用于草浆洗涤的国产四段 (或五段)真空洗浆机，多采用逆流洗涤原理，下面以具备稀释、过滤和置换功能的真空洗浆机组成的多段串联逆流洗涤系统为例进行物料衡算，洗涤的过程流向如图2所示。

图2 多段逆流洗浆图

图2中：

V0，C0—分别表示进入洗浆系统的黑液量 (t黑液/t绝干浆)和固形物浓度 (kg固形物/t黑液);

Vw(k+1)，Cw(k+1)—分别表示进入洗浆系统的液体浓度 (t液体/t绝干浆)和固形物浓度 (kg固形物/t黑液);

Vi，Ci—分别表示第 i段洗浆机出口液体量 (t液体/t绝干浆)和固形物浓度 (kg固形物/t黑液);

Vwi，Cwi—分别表示第i段洗浆机出口滤液量 (t液体/t绝干浆)和固形物浓度 (kg固形物/t黑液)。

对上述过程中的洗浆系统进行物料衡算［1］：

首先，对第i段洗浆机进行液体量衡算：

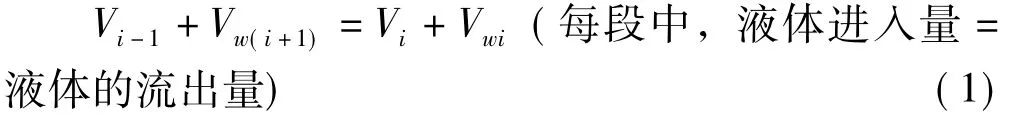
式 (2)中，第i段洗浆机洗涤液体量与洗涤后纸浆液体量之差为一常数，即为稀释因子DF(Dilution Factor)(t水/t绝干浆)。

其次，对第i段洗浆机进行固形物衡算：

令Ri为第i段洗浆机洗涤液比，根据洗涤系统定义有：

依据洗涤工艺，进行实验分析可知，在每段洗涤过程中，洗浆机出口黑液浓度与进入上一段洗浆机的黑液浓度基本相同，有：Ci≈Cwi

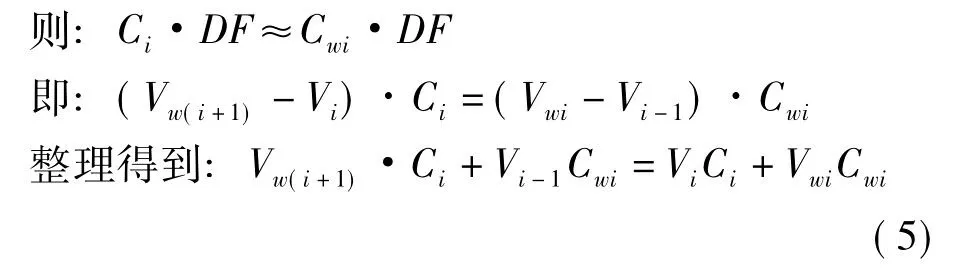
联立式 (4)、式 (5)，得：

两边同时乘以Vi并整理得：

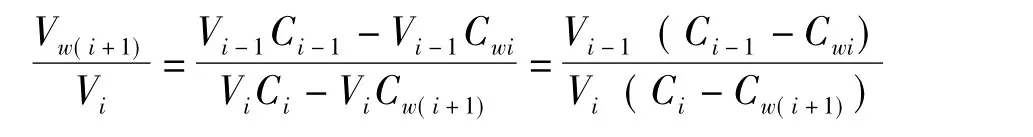
即

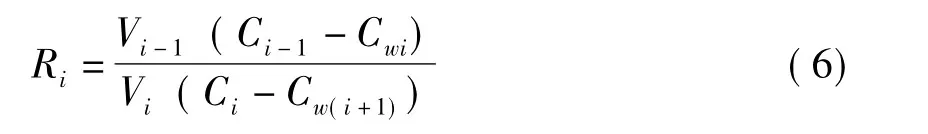
k 段逆流洗浆，将 R1，R2，… Rk－1，Rk连乘，得：

再次，对整个洗浆系统进行固形物衡算：

因为最后一段洗浆机稀释液为清水，即

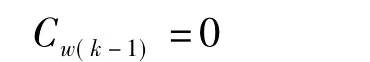
化简式 (7)和式 (8)，两式并联立

因此，

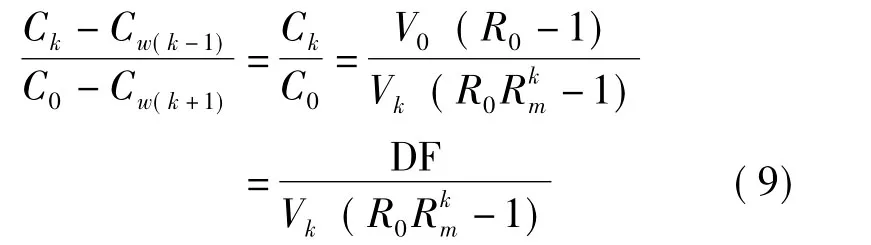
所以，对整个洗涤过程而言，损失的固形物量，即洗后纸浆带走的固形物量为：

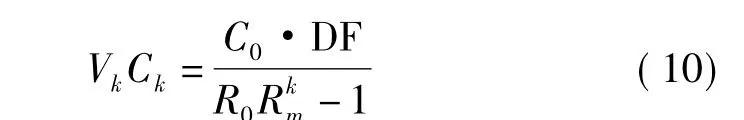
从洗浆系统进入蒸发系统的黑液量及固形物浓度为：

2.2 蒸发系统数学模型

对于麦草制浆产生的黑液，科学有效的处理方法之一是采用碱回收技术，彻底根除黑液污染并回收工业用碱，实现工业用碱和蒸汽的循环利用。但碱回收系统投资很大，而且运行成本较高，投资回收慢［3］，降低其运行成本的有效途径之一是尽可能地提高碱回收车间蒸发工段入效黑液的浓度。这就对浆料洗涤过程的洗涤水用量提出了要求。一般来说，为了将浆料洗干净，要多加水，并延长洗涤时间，这不但造成洗涤效率低，能源消耗大，而且产生的黑液量大，浓度低，加重了碱回收车间蒸发工段的压力和运行费用;为了提高首段黑液波美度，最直接的方法是少加洗涤清水，但又很可能会造成洗后浆残碱量提高和浆料里面附着的有机质 (如木素等)增多，这会明显增加后续漂白工段的药剂使用量，增加漂白工段的负担，并带来更多的环境污染。因此，浆料洗涤过程是一个多指标平衡的过程，也是优化控制的重点和难点［4］。

对蒸发系统进行固形物衡算［1］：

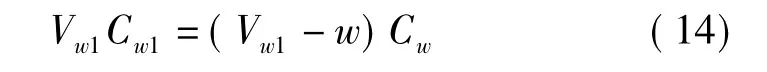
可得：

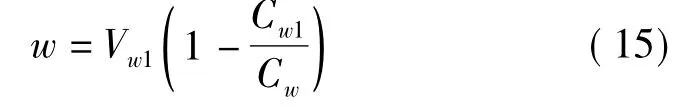
式中，w—蒸发水总量 (t水/t绝干浆);

Cw—出蒸发系统的固形物浓度 (kg固形物/t液体)。

蒸汽消耗量为：G=w/β

式中，G—蒸汽消耗量 (t);

β—每吨蒸汽所能蒸发的水量 (t水/t汽)。

2.3 目标函数——用水费用的确立

对纸浆洗涤和蒸发系统，与稀释因子有关的费用有：固形物损失费用，蒸发系统加热蒸汽费用，洗涤热水费用，从蒸发系统中回收的冷凝水费用。

整个洗浆以及蒸发系统用水费用的目标函数可表示为：

式中，F—总费用 (元/t浆);

a1—加热蒸汽费用系数 (元/t);

a2—洗涤热水费用系数 (元/t);

a3—固形物费用系数 (元/t);

a4—从蒸发系统中回收的冷凝水费用系数

(元/t);

其中，V0，C0，Cw，β，a1，a2，a3，a4等参数均可在实际生产过程中测量得到，或根据生产工艺条件等来确定。f是以稀释因子DF为参数变量的目标函数。本课题通过罚函数法对目标函数进行优化。

3 优化模型求解

3.1 纸浆洗涤用水具体模型

以山东某企业的一个四段逆流洗浆工段为例，进行费用的优化。根据工艺和设计数据，得到以下参数：原料中V0=6 t黑液/t绝干浆，C0=200 kg固形物/t黑液;四段逆流洗浆V1=V2=V3=V4=5 t黑液/t绝干浆;黑液蒸发后要求达到的固形物浓度Cw=600 kg固形物/t黑液;每千克蒸汽蒸发的水量β=3.5 t水/t汽;加热蒸汽费用系数a1=4元/t;洗涤热水费用系数a2=0.08元/t;固形物损失费用a3=0.05元/t，从蒸发系统中回收的冷凝水价值系数a4=0.4元/t，其中，加热蒸汽、冷凝水、洗涤热水费用系数是依据目前企业供热蒸汽实际情况选取的，按照50∶5∶1进行。

因此，整个洗浆以及蒸发系统用水费用的目标函数可表示为：

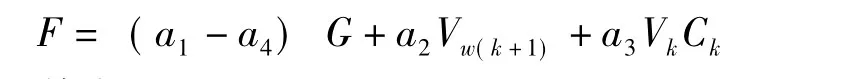
其中，

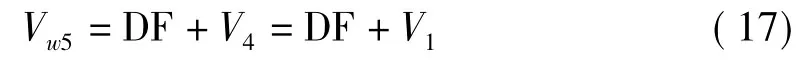
综合式 (17)、式 (18)、式 (19)及相应参数，可以得到目标函数为：

根据实际工艺要求，由稀释因子构成的约束条件为：0＜DF＜6。

纸浆洗涤用水优化模型可表示为：

表1 优化结果

3.2 稀释因子的罚函数优化

罚函数法［5］是一种处理约束优化问题的有效方法，其基本思想是给目标函数增加一个惩罚项，构成罚函数，把原问题转化为以罚函数为目标函数的新的无约束优化问题来求解，通过对不满足条件的解施以惩罚，达到淘汰不可行解、得到最优解的目的。

已知约束条件为：0＜DF＜6

所以有：g1(DF)= －DF＜0，g2(DF)=DF－6≤0

惩罚项为：P(DF，k)=k［max(g1(D)，0)］2+k［max(g2(D)，0)］2

罚函数为：φ(DF，k)=f(DF)+P(DF，k)

罚函数φ(DF，k)对DF进行求导，求出的极小值即为最优的稀释因子，相应可得到纸浆洗涤用水的最优化。采用MATLAB优化工具箱进行求解，优化结果见表1。

4 优化仿真

根据外罚函数算法对已建立纸浆洗涤用水模型进行优化，可求得最优稀释因子DF=3.14619≈3.15(t水/t绝干浆)，在该稀释因子下的总费用为F=f(DF)≈10.92元。优化结果见表1，总费用-稀释因子关系见图3。

如图3所示，总费用是随着约束范围内稀释因子的增加先减小后上升的，即整条目标曲线在约束条件下的最低点坐标约为 (3.15，10.92)，该结果与采用罚函数求出的稀释因子最优解及总费用是十分接近的，误差很小。因此，在实际生产中采用最优稀释因子是可行的。

图3 总费用-稀释因子关系图

5 结语

本课题主要研究了纸浆洗涤过程的用水优化问题，基于浆料洗涤系统整体工程的思想，建立了纸浆洗涤用水和稀释因子的最优化模型，并结合罚函数法对洗浆过程用水进行寻优。结果表明，该方法解决非线性复杂生产过程的优化控制是可行的，在求解精度、满足约束、可靠性等方面，具有较好的通用性，容易求出全局最优的稀释因子，达到总费用最低的目的，可为浆纸企业带来较大的经济效益。

［1］鄢烈祥．制浆厂洗涤用水最优化［J］．湖北工学院学报，1994，9(2)：19．

［2］宗大伟，王孟效．纸浆洗涤过程的DCS方案设计［J］．中国造纸，2004，23(10)：43．

［3］ Louhelainen J，Alen R，Feng Z．Combustion properties of black liquors from alkaline pulping of wheat straw and reed canary grass［J］．Tappi J．，2003，2(10)：53．

［4］ William E J．Multi-component control of brownstock washing［J］．Tappi J．，1993，76(9)：197．

［5］陈宝林．最优化理论与算法［M］．北京：清华大学出版社，1994．

Optimization of the Dilution Factor in Pulp Washing Process

SHAN Wen-juan1，*TANG Wei1，2
(1．Department of Paper making Engineering Shaanxi University of Science and Technology，Xi'an，Shaanxi Province，710021;2．Shaanxi Xi Wei Process Automation Engineering Co．Ltd，Xi'an，Shaanxi Province，712000)

The purpose of the optimal control of pulp washing is not only to ensure the quality of pulp washing，but also to reduce the energy consumption．Water is one of the most important resources;reduce water consumption is to reduce energy consumption．This paper analyzed the material balance in pulp washing and evaporation．The model related dilution factor and washing water was established，the model was optimized by penalty function，which can turn the constrained problem into unconstrained．It showd that the method can find the optimal dilution factor，reduce the consumption，bring greater economic benefits to the enterprises．

pulp washing water;dilution factor;penalty function;optimization

TS736

0254-508X(2012)02-0050-04