采用模式搜索法对轨道炮重要参数的优化设计

刘 文，张海军，白象忠， 张立功

(1.燕山大学 理学院,河北 秦皇岛 066004；2.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004)

近年来随着新技术、新材料不断发展，电磁轨道炮在发射装置、发射质量、弹丸速度和大功率电源等方面的研究取得了一系列成果[1-2]。美国的苏伦斯·利弗莫尔国家实验室和洛斯·阿拉莫斯国家实验室曾合作，将2.2 g的弹丸加速到10 km/s的超高速。国内某研究所建造的国内首台电磁轨道发射试验装置可把0.34 g的弹丸加速到16.8 km/s的速度。弹丸的超高速，使其具有了巨大的动能和极强的穿透力，从而大大提高了武器的射程和威力[3]。

目前对电磁炮的研究方兴未艾，涉及到电磁炮研究的各个领域。而对于弹丸的速度建模问题，Parker认为电磁炮的速度与膛壁烧蚀、等离子体质量增加有关；Ray从运动阻力角度引入与速度有关的阻力项等[4]。但上述研究都是在没有考虑空气阻力的情况下进行的，所以与实际还有一定的差距。作为为高技术高精度的电磁轨道炮，工程上要求更加精确的理论分析与计算。因此，本文在考虑了电枢运动过程中等离子体的粘性阻力、惰性阻力和空气阻力情况下，构建了电磁轨道炮电枢的运动模型，并运用模式搜索法对电磁轨道炮重要参数进行了优化计算。

1 电枢运动模型

1.1 工作原理及对电感梯度的分析

当轨道通过大电流时，电枢受到洛仑磁力的作用沿着轨道向前运动。电枢在整个运行过程中，电流可近似地看作是恒定不变的，那么它蕴藏的磁场能量可表达为：

(1)

式中：E为系统储存的能量，主要为轨道分布电感的磁能；Lr为电感；I为驱动电流。

那么电感可表达为[4]：

(2)

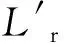
根据电磁理论，电磁力F可表达为[5]：

(3)

式中：电磁力F是电枢在轨道上受到的驱动力。

根据电感理论知识，电感梯度可表达为[6]：

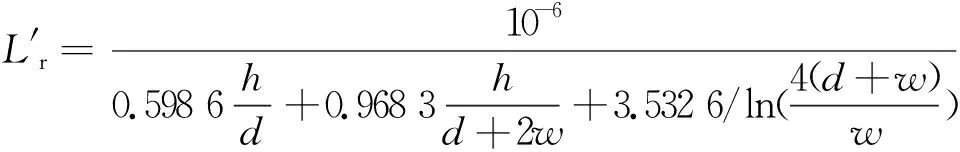
(4)

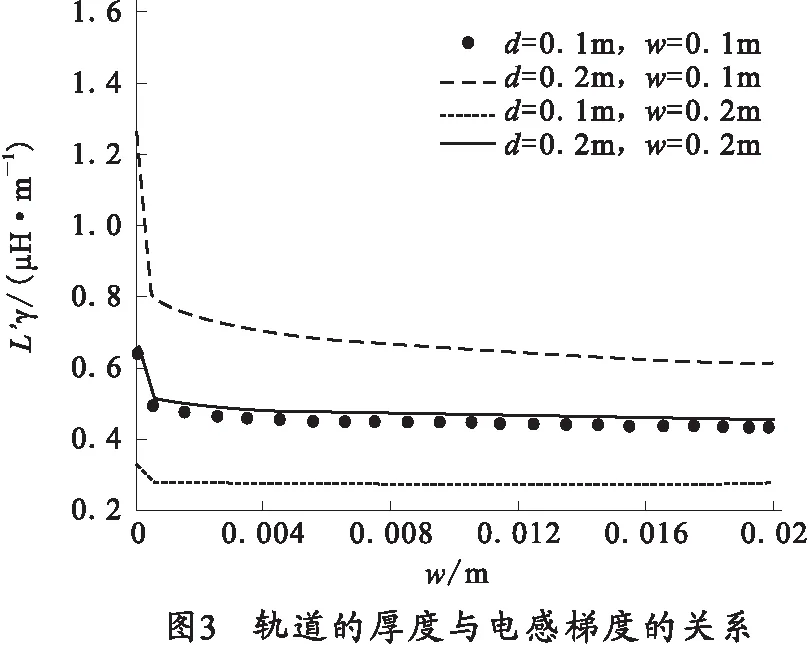
式中：h为轨道的高度；d为两轨道间的距离；w为轨道的厚度。

1.2 电枢运动模型及对电枢阻力的分析

电枢在受到电磁力的作用下，推动它前面的弹丸高速运动，因此，电枢的选择是研究电磁轨道炮的一个重要环节。目前用于电磁轨道炮的电枢主要形式有固体电枢、等离子体电枢和混合电枢等3种，如图4所示。

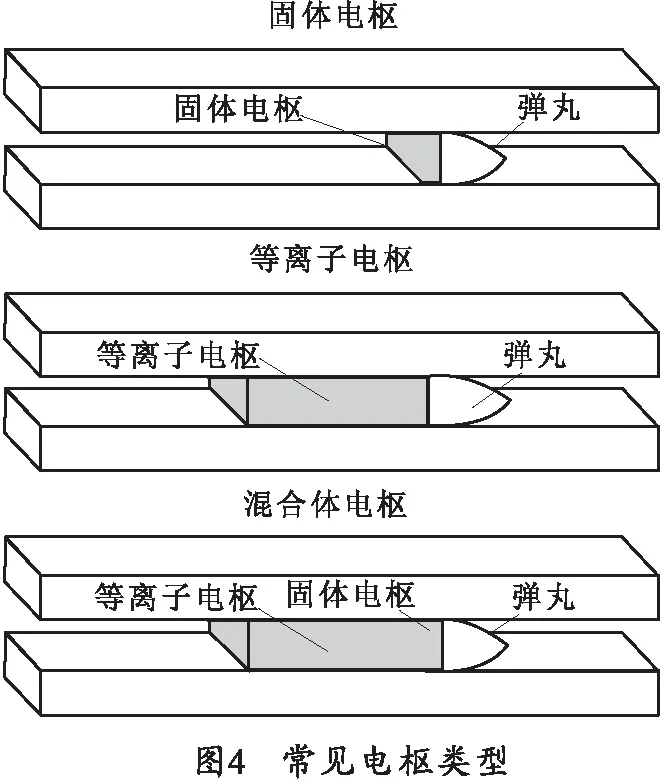
本文所构造的模型采用等离子体电枢。

电枢在大电流通过时，在极短时间内迅速熔化并汽化爆炸，形成等离子体电枢。等离子体电枢在轨道上运行时受到电磁力F的作用；随着电枢中电流的增大和时间的延续，等离子体的温度急骤升高，导致轨道内壁和发射体材料局部融化、蒸发，与等离子区混合，形成粘滞性阻力Fv；部分材料迁移到电枢上，增加了等离子体电枢的质量，形成惰性阻力Fd；实际电磁轨道炮电枢在过程中，还会受到前方的空气阻力Fg。这几种力分别定义如下：

1)粘滞阻力Fv可表达为[10]：

(5)

式中：λ为粘滞因数，与电枢与轨道的加工精度和光滑度有关，在精度和光滑较高情况下，λ=0.012 5；ma为电枢质量；d为导轨间距；h为导轨宽度；v为电枢速度。

2)惰性阻力Fd可表达为[10]：

(6)

电枢质量ma按以下公式求出：

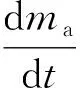
(7)

(8)

式中：α是烧蚀系数，与速度、电枢与轨道的材料有关，通常看作为一个常量，当采用铜材料时，α≈4.7×10-8kg/J；m0为电枢的初始质量，取0.01 kg；Ua是弧压，它的大小是模型合理的关键参数，如果等离子体平稳时，弧压可以通过测量轨道口出两端电压近似得到，而根据澳大利亚坎培拉实验室及其他实验室[5]的试验结果，可以假定炮口电压为常数，一般认为Ua=200 V。

弧压与电枢电阻满足欧姆定律，即：

Ua=IRa

(9)

其中，Ra为电枢电阻。

3)空气阻力Fg为[11]：

空气阻力与速度有关，与电枢的横截面积有关，近似表达式为[6]：

Fg≈1.1ρ0Sv2

(10)

S=dh

(11)

式中：ρ0为空气密度，在标准状况下，空气密度为1.29 kg/m3；S为炮膛的截面积。

等离子体电枢所受的合力为：

F=(mp+ma)a=F-Fv-Fd-Fg

(12)

式中：mp为弹丸质量，这里取值为0.005 kg；a为电枢加速度。

根据式(12)即可得到加速度的表达式为：

(13)

由牛顿定律和运动学公式，得到电枢的瞬时速度和位移分别为：

(14)

式中:v0为电枢的初速度，一般认为v0=0。综合上述式(3),(8),(13),(14)即可得到以下的表达式为：

(15)

2 重要参数优化设计

2.1 模型设计

电磁轨道炮重要参数的优化设计采用模式搜索法，其目的是当弹丸的发射速度最大时，求出最佳的电枢位移量、轨道的间距以及此时弹丸(电枢)的速度。

根据电枢运动方程(5)，电磁轨道炮的优化设计模型如下：

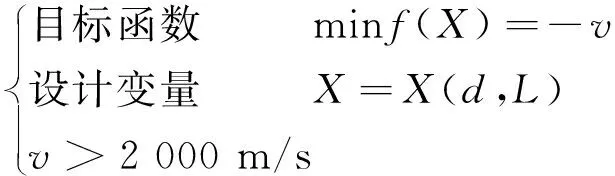
(16)

式中：X为自变量。

2.2 算法步骤[12]

用模式搜索法求无约束问题minf(x),x∈Rn的算法步骤如下：

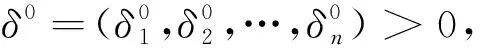
2) 令y=xk；

3) 从y出发，依次作平行于单位矢量ej(j=1,…,n)的轴向探测移动:

4) 令xk+1=y，若f(xk+1)≥f(xk)，则对xk+1沿加速方向pk=xk+1-xk做模式移动，令y=xk+1+γpk，δk+1=δk，k=k+1，转3)，否则转5)；

5)若|δk|<ε，则停止迭代，输出xk，否则当xk+1≠xk时，y=xk+1，δk+1=δk，k=k+1,转3)，当xk+1=xk时，令y=xk+1，δk+1=θδk，k=k+1,转3)。

在算法的应用过程中，通常取加速系数r∈[1,2]，收缩系数θ∈[0.1,0.5]。

3 优化结果及分析

根据表达式(16)优化模型，通过不同的轨道的厚度和轨道的高，采用模式搜索法对电磁轨道炮的重要参数两轨道的间距和电枢运动的位移量进行优化计算，计算结果如表1所示。

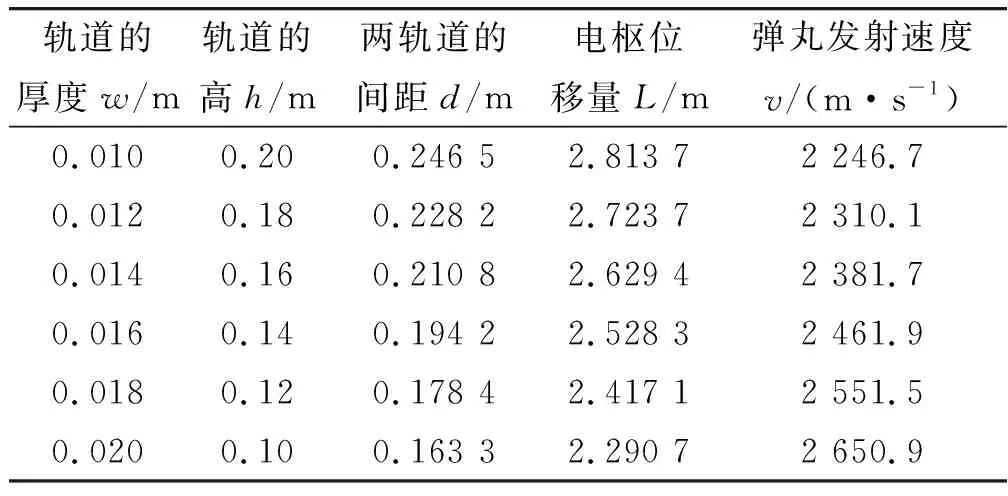
表1 优化结果

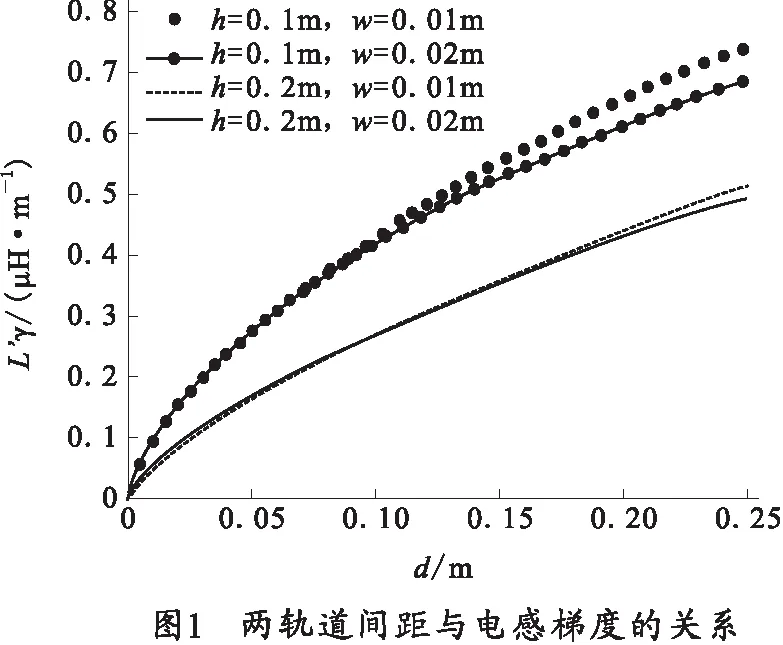
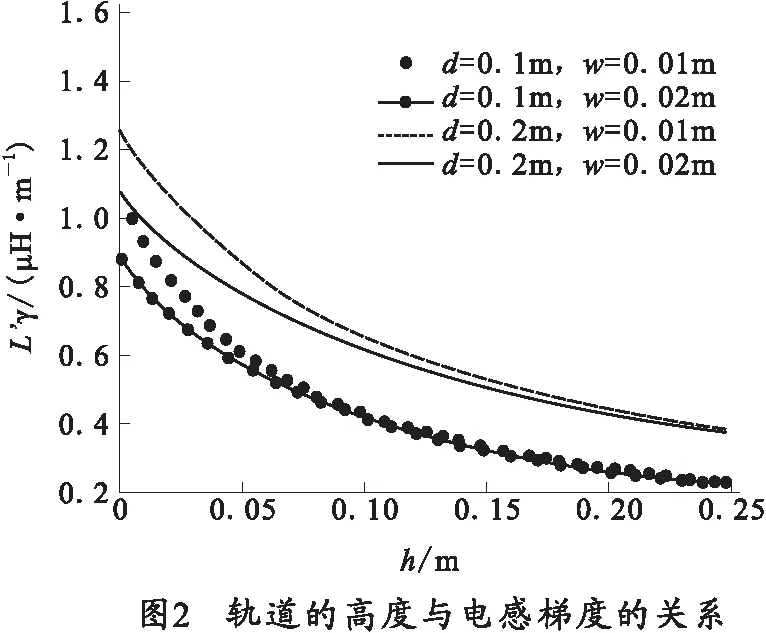
从表1可以看出，当轨道的间距为d=0.163 3 m，电枢位移量为L=2.290 7 m时，弹丸的发射速度将达到最大，其最大值为v=2 650.9 m/s。从构造电枢运动的模型来看，轨道的高度或厚度对弹丸发射速度的影响是相当明显的，通过图1～图3可以看出电感梯度与轨道的间距，轨道的高度和轨道厚度之间的关系。但是表1中的优化结果表明，轨道的高度对电感梯度的影响要比轨道的厚度对电感梯度的影响大得多。而随着轨道高度的减小，轨道的间距和电枢位移量的最佳值也在减小，但弹丸的发射速度却在增加。从图5～图7中可以发现，弹丸的发射速度都是随两个变量(轨道间距和电枢位移量)先增大后减小，引起这种变化的主要原因是离子体电枢在运动过程中受到的阻力(包括粘滞阻力、惰性阻力和空气阻力)作用的结果。

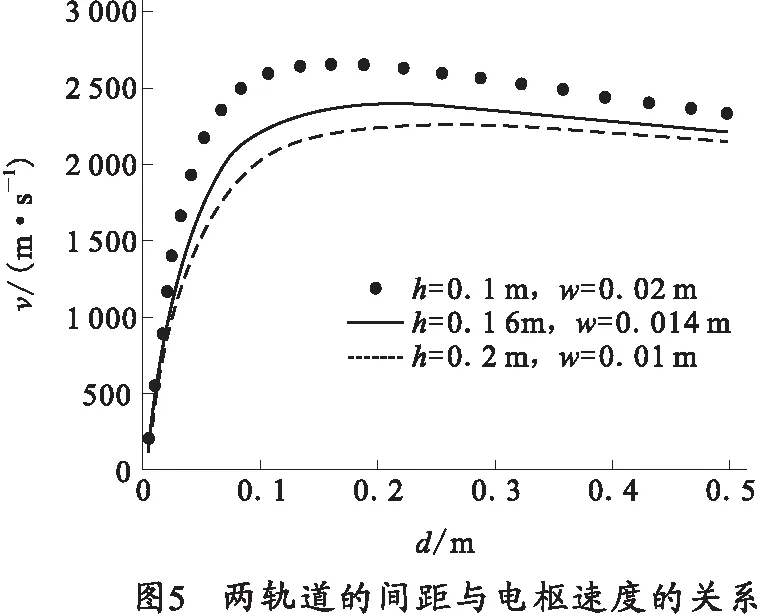
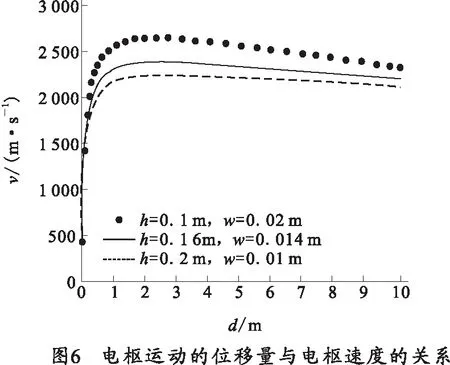
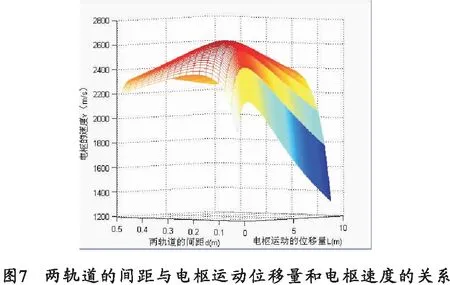
利用模式搜索法对电磁轨道炮进行优化设计及分析，表明了轨道的间距和电枢位移量是影响弹丸发射速度的两个重要参数，如果任意选取这个两个变量的值将直接影响弹丸的发射速度。上述也进一步研究了轨道的高度、轨道的厚度和轨道的间距对电感梯度的影响。通过综合分析在轨道的高度和轨道的厚度取不同值的情况下，从而得到了轨道的间距，电枢位移量以及弹丸发射速度的优化值。

4 结 论

1)根据电磁和电感理论知识，分析了轨道的厚度、轨道的高度以及轨道的间距与电感梯度的关系。

2)在考虑等离子体电枢受到粘滞阻力、惰性阻力和空气阻力的基础上，构建了包括电枢速度、轨道的间距及电枢位移量等重要参数的数学模型。

3)通过用模式搜索法优化计算，得到了当轨道的间距为d=0.163 3 m，电枢位移量为L=2.290 7 m时，弹丸的发射速度将达到最大，其最大值为v=2 650.9 m/s。为提高弹丸的发射速度，应适当选择轨道的高度和轨道的厚度。

4)优化的结果与其他仿真、试验的结果相对比，验证了优化模型的合理性和有效性，为电磁炮关键参数的设计和制造提供了理论上的依据和技术上的支持。

参考文献(References)

[1] Fail H D.A dvances in electrom agnetic launch science and technology and its application s[J]. IEEE Transaction on Magnetics. 2009,45(1): 225-230.

[2] 王静端.电磁发射技术的发展及其军事.应用火力与指挥控制[J].2001, 26(3): 5-7.

WANG Jing-duan. The development and application of military electromagnetic emission technology. Fire Control & Comm and Control[J] .2001, 26(3):5-7.

[3] 刘文,李敏,白象忠,张海军.电磁炮发射轨道受指数函数磁压力的变形计算[J].哈尔滨工业大学学报.2010，42(8).1-2.

LIU Wen,LIN Min,BAI Xiang-zhong,ZHANG Hai-jun.Deformation calculation of electromagnetic Launcher's rail subjected to exponential magnetic pressure[J]. Journal of HaRBin institute of technology. 2010,42(8):1-2.

[4] 王莹 肖锋.电磁原理[M]. 北京:国防工业出版社. 1995:17-18.

WANG Ying,XIAO Feng.The electromagnetic gunrails theory[M] National Defense Industry Press.Bei Jing 1995.17-18.

[5] 姜仲秋,汤承林.电磁发射效率与激励电流关系的仿真[J].四川兵工学报. 2010, 31 (3):4-7.

JIANG Zhong-qiu,TANG Cheng lin.The simulation of electromagnetic emission efficiency and between the excitation current[J].Si Chuan Acta Armamentarii.2010, 31 (3):4-7.

[6] Asgharkeshtkar, SadjadBayati, AhmadKeshtkar. Derivation of a formula for inducatance gradie-nt using intelligent fstimation methed[J]. IEEE Transactions on Magnetaics. 2009, 45(1): 305-5 98.

[7] Asghar Keshtkar. Effect of rail dimension on current distribution and inductance gradient[J]. IEEE Transactions on Magnetaics. 2005, 41(1): 383-385.

[8] Asghar keshtkar,Toraj Maleki,Ali Kalantarnia, Ah-mad Keshtkar.determination of optimum rail di-mensions in railgun by lagrange's equations[J].IEEE Transactions on Magnetaics. 2009, 45 (1):595-597.

[9] Thomas G.Engel,Jesse M.Neri,William C. Nunnally. Efficiency and scaling of constant inductance gradient dc electromagnetic launchers[J]. IEEE Transactions on Magnetaics. 2006,42(8): 2043-2048.

[10] 杨玉东,王建新.电磁炮发射原理数值建模与分析[J].火炮发射与控制学报. 2008 (4):9-11.

YANG Yu-dong,WANG Jian-xin.Numerical modeling and analysis on em gun firing principle[J]. Journal Of Gun Launch and Control.2008(4):9-11.

[11] 杨玉东,王建新,薛文.轨道炮动态负载特性的分析与仿真[J].兵工学报. 2010, 31 (8): 1029-1030.

YANG Yu-dong,WANG Jian-xin,XUE Wen.Simulation and analysis for dynamic load characteristic of rail-gun[J].Acta Armamentarii.2010,31(8):1029-1030.

[12] 龚纯 王正林 编著.精通MATLAB最优化计算[M]. 北京:电子工业出版社.2009,130-131.

GONG Chun WANG Zheng-lin. Optimization calculation with matlab[M] Publishing House of Electronics Industry.Bei Jing 2009,130-131.