基于固定目标式检测火箭炮方向调炮精度研究

何一陆,朱志敏，范 继

(1.湖北江山重工有限责任公司，湖北 襄阳 441057；2.西北机电工程研究所，陕西 咸阳 712099)

目前利用数字经纬仪对火箭炮的调炮精度进行检测已成为成熟技术，但是，当检测现场无数字经纬仪或不具备使用数字经纬仪的条件时，可利用象限仪检测火箭炮的高低调炮精度；利用固定目标方式检测火箭炮的方向调炮精度。用象限仪检测高低调炮精度时可直接读取象限仪的测量数值，方法比较简单，其检测精度取决于象限仪的精度和读取误差；用固定目标式检测火箭炮的方向调炮精度时，固定目标与火箭炮的距离、火箭炮相对固定目标的方位等因素，对检测精度都有影响。以下主要讨论用固定目标式检测火箭炮方向调炮精度时的方法和注意事项及影响检测精度的因素。

1 检测场地和火箭炮停放要求

利用瞄准镜和野外的一个可观测目标进行火箭炮方向调炮精度检查时，要求地面坚实、地面坡度小于火箭炮使用环境对地面坡度的要求；场地面积要求火箭炮能自由的驶入、驶出，并可在场地上对火箭炮进行调头等操作；场地至少有一面视野开阔，且在大于2～3 km处有1个可见的固定观测目标。

火箭炮停放在场地的一端，炮尾大致朝向有固定观测目标的方向；调炮前按操作规程的要求对火箭炮进行支撑和固定。

2 调炮误差检测操作

将经过瞄校的瞄准镜正确地安装在瞄准具上，操作人员在操瞄踏板上站稳并用手扶住可靠的物体，确保在调炮过程中的安全，在调炮和检测过程中操作人员不能离开操瞄踏板，以防人员走动对调炮误差的影响。

火箭炮按操作规程进行调炮前的准备后，首先进行一次收炮操作，收炮操作完成后，操作人员将瞄准镜的纵向、横向调平，并将瞄准镜的目镜对准固定观测目标上的一个特殊点，此时读取瞄准镜的方向分划值并记为M0，然后，火箭炮调炮到一个射击诸元(高低角N01、方向角M01)，重新将瞄准镜的纵向、横向调平，并重新将瞄准镜对准视野开阔处的固定观测目标上的同一特殊点，读取瞄准具的高低分划值并记为N11，读取瞄准镜的方向分划值并记为M11，此时的调炮误差分别为：

高低误差：

N1=N11-N01

(1)

方向误差：

M1=(M11-M0)-M01

(2)

当这个射击诸元调炮到第n次，并重复以上操作和记录时有以下关系式：

高低误差：

Nn=Mn1-N01

(3)

方向误差：

Mn=(Mn1-M0)-M01

(4)

高低误差平均值：

(5)

方向误差平均值：

(6)

均方差表达的高低角、方向角调炮误差为：

高低调炮误差：

σ1δN=

(7)

方向调炮误差：

σ1δM=

(8)

3 相对位置不同对检测精度的影响

在检测火箭炮调炮精度时，实际需要检测的是基准管的运动精度，由于在基准管上不方便观察和记录，所以，利用经过瞄校后的瞄准镜光轴线与基准管光轴线在垂直面内、水平面内平行的原理，当被瞄物的固定目标点与火箭炮的距离相对于瞄准镜与基准管的距离较远时，用瞄准镜来观测固定目标以替代基准管观测目标。然而，当火箭炮相对固定目标的位置不同时，其瞄准镜在运动轨迹上的各个点对固定观测目标点的几何关系也不同，所以在各个点的检测误差也有相应的差异。以下对火箭炮相对固定目标的位置不同时，在调炮过程中瞄准镜运动轨迹上的各个点的检测误差进行分析。

如图1所示，A点是检测调炮精度时用于被观测的固定目标点，B点为火箭炮方向调炮到某一点时瞄准镜的位置，C点为火箭炮初始时瞄准镜位置，D点为火箭炮定向器或瞄准镜在调炮运动时的回转中心。角度α为火箭炮方向角从初始位置C运动到某一点B时瞄准镜重瞄固定点A时的瞄准误差。

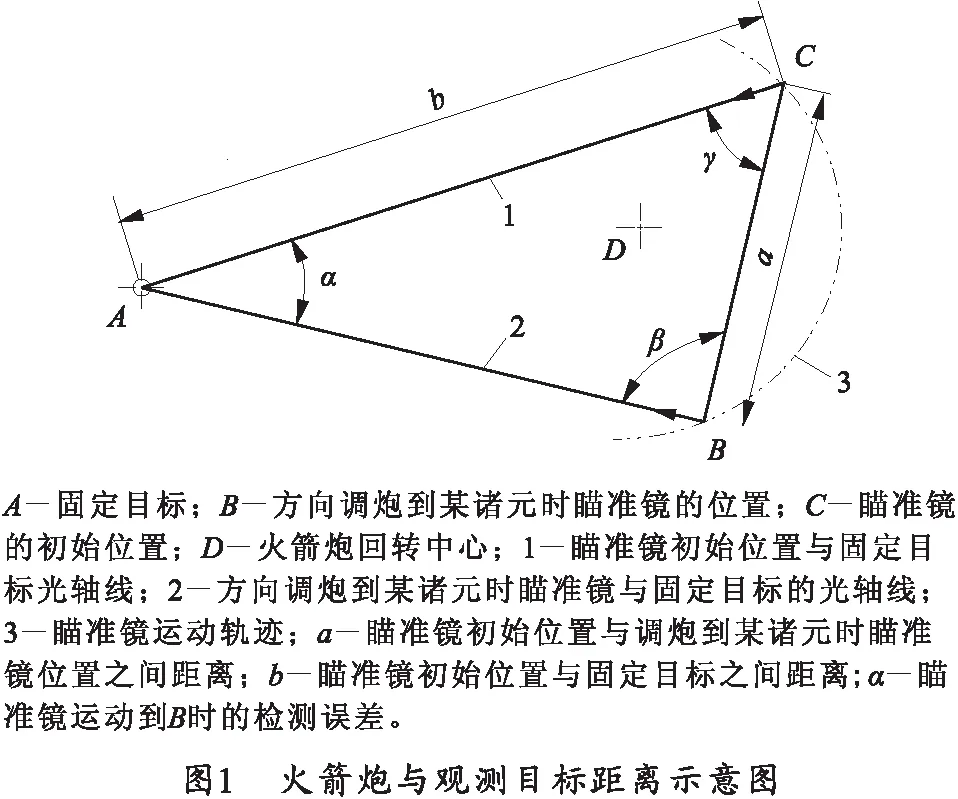
3.1 检测误差最大时固定观测目标与火箭炮的相对位置

如图1所示，角α为检测误差，根据正弦定律有：

(9)

整理得：

(10)

在式(10)中，当火箭炮与固定目标的位置确定后,a、b为定值，所以当sinβ最大时sinα的值最大。

β的取值范围为0°～180°，由正弦函数得，只有当β=90°时,sinα最大，即测量误差值α最大。

同理，也只有当γ=90°时sinα为最大，即测量误差值α最大。

因此，为了减少瞄准镜的瞄准误差，在选择固定观测目标与火箭炮的相对位置时尽可能使β≠90°或γ≠90°。即∠ABC≠90°或∠BCA≠90°。

3.2 检测误差最小时固定观测目标与火箭炮的相对位置

根据式(10)，当β=0°时sinα最小，即测量误差值α=0。

图2是当β=0°或γ≠0°时的几何图形，从图中可以看出当被观测固定目标A在B、C的延长线上时β=0°，此时的检测误差值α=0。

根据以上分析，得出以下结论：

1) 当A、B、C三点的连线为一条直线时，B点的测量误差为零。

2)测量误差α与角度β或角度γ的关系符合正弦函数分布，根据图3所示得如下关系式：

当0°≤β≤180°时，函数曲线如图3 所示，从图中可以看出，在0°～180°范围内，当β的值越远离，测量误差α越小。

3)只有当β或γ等于90°时，B与C两点的测量误差α最大。

4 检测误差估算

经过以上分析，得到了产生最大检测误差时的条件。如果知道了固定目标距火箭炮、瞄准镜距火箭炮回转中心在不同距离条件下的最大检测误差的估算值，在作调炮精度检测工作时就可以避免最大误差，或者排除最大误差，或者对检测的调炮误差进行修正，从而获得更准确的调炮精度检测值。

下面以图2为例，对几种条件下的最大方向调炮精度检测误差进行计算。

如图2所示，ΔABC中，在当∠ABC=90°，测量误差最大，α与边a和边b有如下关系：

(11)

整理后得：

(12)

分别取a=300 mm、a=800 mm、a=1 000 mm、a=1 300 mm、a=1 500 mm，b=1 km、b=2 km、b=2.5 km、b=3 km、b=3.5 km、b=4 km、b=5 km、b=6 km，根据式(12)计算得到表1。

表1 在最大检测误差条件下相关尺寸时的检测误差

5 结束语

本文是在工作实践的基础上，总结了用固定目标方式检测火箭炮方向调炮精度的方法及采用这种检测方法时可能产生最大检测误差和最小检测误差时火箭炮与固定目标的相对位置。希望对各位读者在今后的工作中有所帮助，并希望与各位读者对此类问题进行进一步的探讨。

参考文献(References)

[1] 罗鸿飞, 张英堂, 任国全,等. 基于空间坐标解算的火炮调炮精度检测方法研究[J]. 火炮发射与控制学报, 2007(3): 50-52.

LUO Hong-fei, ZHANG Ying-tang, REN Guo-quan,et al. Research on measuring method of gun rotated accuracy based on spatial coordinate algorithm[J]. Journal of Gun Launch & Control, 2010(3): 50-52.(in Chinese)

[2] 曾刊, 赖文娟. 双经纬仪调炮精度检测系统[J]. 兵工自动化, 2011(7): 73-75.

ZENG Kan, LAI Wen-juan. Gun slaving precision detecting system of double-theodolite[J]. Ordnance Industry Automation, 2011(7): 73-75. (in Chinese)

[3] 韩淑文，蔡世伟. 对某火箭炮批产中自动调炮精度的技术研究与实践验证[J]. 新技术新工艺，2010(2): 81-84.

HAN Shu-wen,CAI Shi-wei. Technical research and practical test for the accuracy of automatic gun adjustment in the batch-production of a kind of rocket launcher[J]. Technology & New Process，2010(2): 81-84. (in Chinese)

[4] 李平, 王英. 基于数字式经纬仪检测的调炮精度测量装置[J]. 火力与指挥控制， 2010(S1): 96-98.

LI Ping, WANG Ying. Gun Slaving accuracy measurement unit based on digital theodolite detect[J]. Fire Control and Command Control, 2010(S1): 96-98. (in Chinese)

[5] 孙泽林, 王昭, 翟唤春. 双经纬仪交会测量火炮调炮精度的误差分析与抑制[J]. 光学精密工程,2011:2434-2441.

SUN Ze-lin, WANG Zhao, ZHAI Huan-chun. Analysis and control of error on two theodolite intersection measurement for gun rotated accuracy of artillery[J]. Optics and Precision Engineering, 2011:2434-2441. (in Chinese)